জ্যামিতি কাকে বলে
এই টিউটোরিয়ালটি শেষে-
জ্যামিতি কি তা বর্ণনা করতে পারা যাবে।
জ্যামিতি কাকে বলে তা ব্যাখ্যা করতে পারা যাবে।
জ্যামিতির মৌলিক উপাদানগুলোকে সংজ্ঞায়িত করতে পারা যাবে।
জ্যামিতি (Geometry) কি?
গণিতের যে শাখা আকার-আকৃতি, পরিমাপ, স্থান এবং বস্তুসমূহের মধ্যেকার পারস্পারিক সম্পর্ক নিয়ে আলোচনা করে তাকে জ্যামিতি বলে।
জ্যামিতি স্পেস (space) সম্পর্কিত ধারণা নিয়ে কাজ করে। এটি স্পেসের গুণগত বৈশিষ্ট্য বিশ্লেষণ করে যা আমাদের চারপাশের পৃথিবীকে বুঝতে সাহায্য করে।

জ্যামিতি শব্দের উৎপত্তি
জ্যামিতি হলো গণিত এর অন্যতম একটি পুরাতন শাখা। Geometry এর প্রতিশব্দ হলো জ্যামিতি। গ্রিক শব্দ geo এর ইংরেজি প্রতিশব্দ earth যার বাংলা অর্থ ভূমি এবং আরেকটি গ্রিক শব্দ metron এর ইংরেজি প্রতিশব্দ measurement যার বাংলা অর্থ পরিমাপ। এই দুইটি ভিন্ন শব্দ একত্রিত হয়ে geometry শব্দের উৎপত্তি; যার অর্থ দাঁড়ায় ভূমির পরিমাপ।
জ্যামিতির ইতিহাস
প্রাচীন মিশরীয় ও ব্যাবিলনীয় সভ্যতায় জ্যামিতির ব্যবহার দেখা যায়। প্রাচীনকালে ভূমি জরিপ ও নির্মাণের কাজে জ্যামিতির ব্যবহার শুরু হয়। তবে, প্রাচীন গ্রিসে জ্যামিতির একটি সুসংহত রূপ তৈরি হয়।
ইউক্লিড নামে একজন গ্রিক গণিতবিদ জ্যামিতির মৌলিক ধারণাগুলো তাঁর 'এলিমেন্টস' নামক গ্রন্থে লিপিবদ্ধ করেন যা 'ইউক্লিডিয়ান জ্যামিতি' নামে পরিচিত।
একারণে, প্রাচীন গ্রিসবাসীরা জ্যামিতি ব্যবহার নিখুঁতভাবে ভূমির পরিমাপ করতে পারতেন।
জ্যামিতির শ্রেণিবিভাগ
জ্যামিতিকে একদম সুনির্দিষ্টভাবে শ্রেণিকরণ করা একটু কঠিন। তবে একে নিম্নলিখিতভাবে শ্রেণিকরণ করা হয়ে থাকে:
ইউক্লিডিও জ্যামিতি (Euclidean geometry)
এটি সবচেয়ে পরিচিত এবং বহুল ব্যবহৃত জ্যামিতি।
- দ্বিমাত্রিক জ্যামিতি বা সমতল জ্যামিতি (2D Geometry)
- ত্রিমাত্রিক জ্যামিতি বা ঘন জ্যামিতি (3D Geometry)
অ-ইউক্লিডিও জ্যামিতি (non-Euclidean geometry)
এটি ইউক্লিডিও জ্যামিতির কিছু স্বতঃসিদ্ধ মানে না। অ-ইউক্লিডিও জ্যামিতির মধ্যে রয়েছে:
- রিম্যানিয় জ্যামিতি (Riemannian geometry)
- লোবাচেভস্কিয় জ্যামিতি (Lobachevsky geometry)
স্থানাঙ্ক জ্যামিতি
এটি বীজগণিতের মাধ্যমে জ্যামিতিক আকার ও স্থান নিয়ে আলোচনা করে।
ডিফারেনশিয়াল জ্যামিতি
এটি ক্যালকুলাসের মাধ্যমে বক্ররেখা ও পৃষ্ঠের বৈশিষ্ট্য নিয়ে আলোচনা করে।
ইউক্লিডিও জ্যামিতি সম্পর্কে নিচে সংক্ষিপ্ত আকারে ধারণা দেওয়া হলো।
ইউক্লিডিও জ্যামিতি
ইউক্লিড তার তের খণ্ডের "Elements" গ্রন্থের প্রথম খণ্ডের শুরুতেই জ্যামিতির মৌলিক বিষয় বিন্দু, রেখা এবং তলের সংজ্ঞা দিয়েছেন। যদিও আধুনিক গণিতে এসব সংজ্ঞা স্থান বিশেষে কিছুটা অসম্পূর্ণ, তবুও এগুলোই জ্যামিতির মূল ভিত্তি।
ইউক্লিডিও সংজ্ঞা
ইউক্লিড প্রদত্ত সংজ্ঞাসমূহ নিম্নরূপঃ
- যার কোন অংশ নাই, তাই বিন্দু।
- রেখার কোনো প্রান্ত বিন্দু নেই।
- যার কেবল দৈর্ঘ্য আছে, কিন্তু প্রস্থ ও উচ্চতা নেই, তাই রেখা।
- যে রেখার উপরিস্থিত বিন্দুগুলো একই বরাবরে থাকে, তাই সরলরেখা।
- যার কেবল দৈর্ঘ্য ও প্রস্থ আছে, তাই তল
- তলের প্রান্ত হলো রেখা।
- যে তলের সরলরেখাগুলো তার উপর সমভাবে থাকে, তাই সমতল।
ইউক্লিডিও স্বতঃসিদ্ধ
প্রকৃতপক্ষে, যেকোনো গাণিতিক বিশ্লেষণে গণিতের কিছু কিছু প্রাথমিক ধারণাকে স্বীকার করে নেওয়া হয়। ইউক্লিড এগুলোকে স্বতঃসিদ্ধ বলেছেন।
ইউক্লিড প্রদত্ত স্বতঃসিদ্ধগুলো নিম্নরূপঃ
- যে সকল বস্তু একই বস্তুর সমান, সেগুলো পরস্পর সমান।
- সমান সমান বস্তুর সাথে সমান বস্তু যোগ করা হলে যোগফল সমান।
- সমান সমান বস্তু থেকে সমান বস্তু বিয়োগ করা হলে বিয়োগফল সমান।
- যা পরস্পরের সাথে মিলে যায়, তা পরস্পর সমান।
- পূর্ণ তার অংশের চেয়ে বড়।
ইউক্লিডিও স্বীকার্য
আধুনিক গণিত তথা জ্যামিতিতে প্রাথমিক ধারণা হিসাবে বিন্দু, রেখা এবং সমতলকে গ্রহণ করে এদের কোনো কোনো বৈশিষ্ট্যকে স্বীকার করে নেওয়া হয়। জ্যামিতির এইসব স্বীকৃত বৈশিষ্ট্যগুলোই স্বীকার্য হিসাবে পরিচিত। তবে বাস্তব ধারণা ও বিশ্লেষণের সাথে মিল রেখেই এইসব স্বীকার্যগুলো পরিপূর্ণরূপ লাভ করেছে।
ইউক্লিড প্রদত্ত স্বীকার্যগুলো নিম্নরূপঃ
- একটি বিন্দু থেকে অন্য একটি বিন্দু পর্যন্ত একটি সরলরেখা আঁকা যায়।
- খণ্ডিত রেখাকে যথেচ্ছভাবে বাড়নো যায়।
- যে কোনো কেন্দ্র ও যেকোনো ব্যাসার্ধ নিয়ে বৃত্ত আঁকা যায়।
- সকল সমকোণ পরস্পর সমান।
- একটি সরলরেখা অপর দুইটি সরলরেখাকে ছেদ করলে এবং ছেদকের একই পাশের অন্তঃস্থ কোণদ্বয়ের সমষ্টি দুই সমকোণের চেয়ে কম হলে, রেখা দুইটিকে যথেচ্ছভাবে বাড়ানো হলে যেদিকে কোণের সমষ্টি দুই সমকোণের চেয়ে কম, সেদিকে মিলিত হয়।
জ্যামিতির মৌলিক উপাদান
জ্যামিতির মৌলিক উপাদানগুলো নিম্নরূপ:
- বিন্দু
- রেখা
- কোণ
- সমতল
বিন্দু
যার কেবল অবস্থান আছে কিন্তু দৈর্ঘ্য, প্রস্থ ও উচ্চতা বলতে কিছুই নেই তাকে বিন্দু বলে।
অন্যভাবে বলা যায়, দুইটি রেখা পরস্পর মিলিত হলে, মিলিত স্থানে একটি বিন্দু উৎপন্ন হয়।
অর্থাৎ, পরস্পরচ্ছেদী দুইটি সরলরেখার ছেদস্থানই একটি বিন্দু। যেমন, একটি বইয়ের দুই ধার বইটির একটি কোণায় একটি বিন্দুতে মিলিত হয়।
গণিতে বিন্দুকে কেবল অবস্থান হিসাবে বিবেচনা করা হয়। অর্থাৎ বিন্দুর কেবল অবস্থান আছে বলে ধরা হয়। তাছাড়া এর কোন দৈর্ঘ্য বা প্রস্থ বা উচ্চতা বলতে কিছুই নেই। অতএব বিন্দুর মাত্রা শুণ্য।
একটি সমতলের দুইটি ভিন্ন বিন্দু দিয়ে কেবল একটি সরলরেখা আঁকা যায়।
অন্যভাবে বলা যায়, একটি সরলরেখার দৈর্ঘ্য ধীরে ধীরে কমালে সর্বশেষে সরলরেখাটি একটি বিন্দুতে পরিণত হয়।
জগত হলো সকল বিন্দুর সেট।
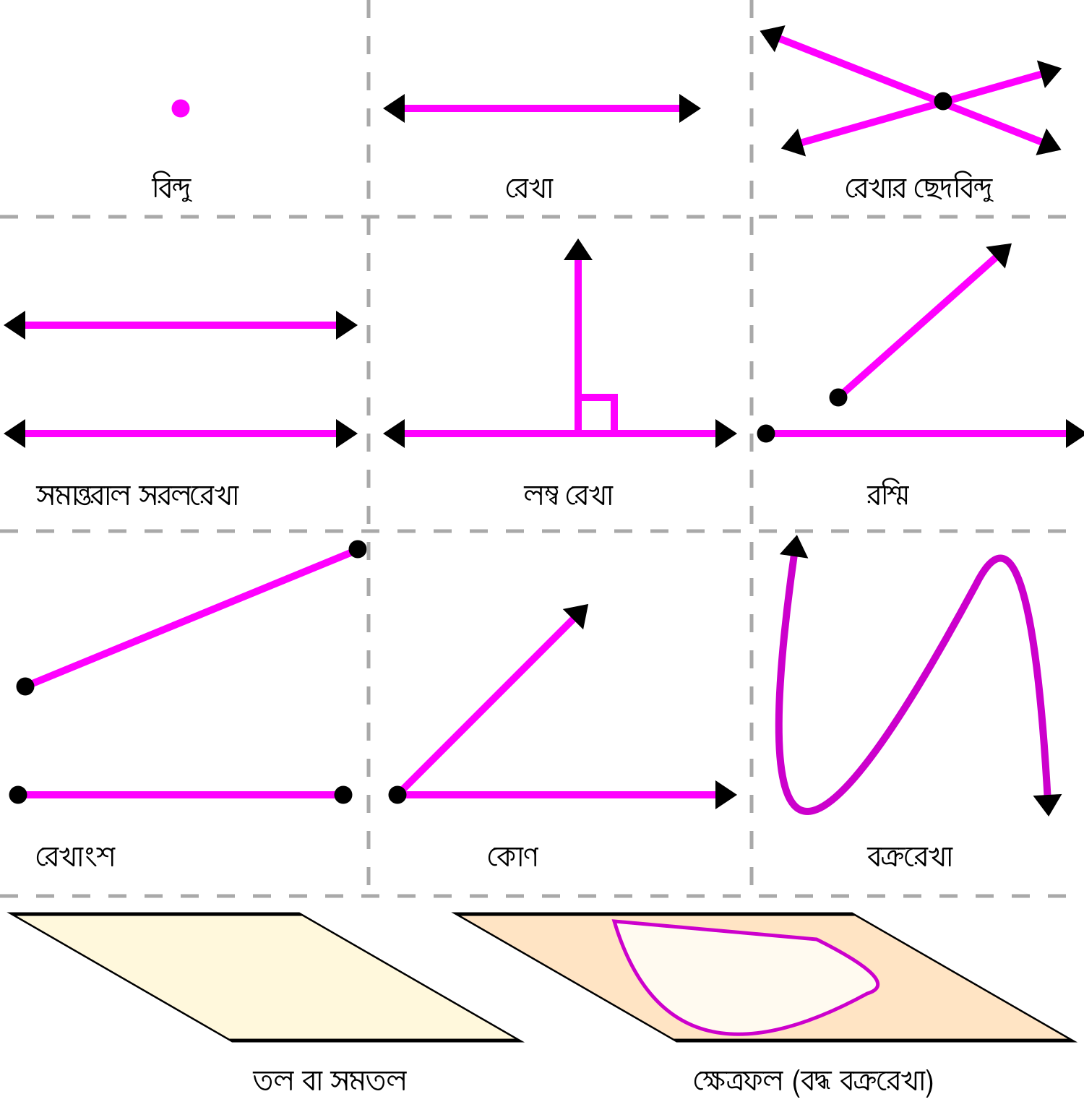
রেখা
যার অসীম দৈর্ঘ্য আছে কিন্তু, প্রস্থ ও বেধ নেই তাকে রেখা বলে।
একাধিক বিন্দু উভয়দিকে সোজাসুজি অসীম পর্যন্ত পরস্পর সংযুক্ত হয়ে যে পথ তৈরি হয়, তাই রেখা। রেখার চলার পথ সোজা (straight) বা সরল, তাই একে সরলরেখাও বলা হয়। সুতরাং বলা যায়, রেখা হলো উভয়দিকে সোজাসুজি বিন্দু চলার পথ।

অন্যভাবে বলা যায় ...
রেখা হলো প্রস্থ বা বেধ বিহীন একটি দৈর্ঘ্য যা উভয়দিকে সোজাসুজি অসীম পর্যন্ত ক্রমবর্ধমান। রেখার কোন প্রান্ত বিন্দু নেই। এটি সবসময় অসীম পর্যন্ত ক্রমবর্ধমান।
সুতরাং একটি রেখার মধ্যে নিম্নের ধারণা দুইটি অন্তর্ভুক্তঃ
- রশ্মি
- রেখাংশ
অতএব, এক কথায় বলতে গেলে- রেখা হলো একদম সোজা উভয়দিকে ক্রমবর্ধমান প্রান্তহীন পথবিশেষ। সুতরাং এর কেবল দৈর্ঘ্য আছে। তাই রেখা হলো একমাত্রিক জ্যামিতির অন্তর্ভুক্ত। চিত্রে একটি রেখা দেখানো হয়েছে যা উভয়দিকে অসীম পর্যন্ত ক্রমবর্ধমান।
মনেকরি, একটি রেখার উপর A ও B দুইটি ভিন্ন বিন্দু।
এটিকে পড়া হয় AB একটি রেখা এবং লিখে বুঝানো হয়।
কোণ
দুইটি রশ্মির প্রান্তবিন্দু একই বা সাধারণ (common) হলে উৎপন্ন জ্যামিতিক আকারকে কোণ বলে।
রশ্মি দুইটিকে কোণের বাহু বলা হয়। আর সাধারণ বিন্দুটি কোণের শীর্ষ বলে পরিচিত। রশ্মি দুইটি একে অপরের সাথে কী পরিমানে আনত, তা দিয়েই কোণের পরিমাপ বুঝানো হয়।
সমতল
এক সেট রেখাকে একটার পর একটা সাজালে একটি সমতল উৎপন্ন হয়।
অন্নভাবে বলা যায়, সমতল হল দ্বি-মাত্রাবিশিষ্ট উঁচু নিচু নয় এমন সমান তল (flat surface) যা উভয়দিকে অসীম পর্যন্ত ক্রমবর্ধমান। এর কেবল দৈর্ঘ্য ও প্রস্থ আছে। তাই সমতল দ্বিমাত্রিক জ্যামিতির অন্তর্ভুক্ত।
সুতরাং সমতলের মাত্রা দুটি হল দৈর্ঘ্য ও প্রস্থ।
দৈর্ঘ্য ও প্রস্থ অবশ্যই একই সমতলে থাকবে।
এটি দৈর্ঘ্য ও প্রস্থ বরাবর অসীম পর্যন্ত বিরাজমান।
সকল দ্বিমাত্রিক চিত্র সমতলে অবস্থিত।
চিত্রে তিনটি সমান্তরাল সমতল দেখানো হলো।

তাছাড়া, জ্যামিতির মৌলিক উপাদানগুলোর সাথে বক্ররেখা, তল ও ঘনবস্তু নিবিড়ভাবে জড়িত। নিচে সংক্ষেপে এগুলো বর্ণনা করা হলো।
বক্ররেখা
বক্ররেখা হলো বিন্দু চলার একটি বাঁকা পথ যা কতকগুলো বিন্দু পরস্পর যুক্ত হয়ে তৈরি হয়। বক্ররেখা প্রতিনিয়তই দিক পরিবর্তন করে। বক্ররেখার কেবল দৈর্ঘ্য আছে। সুতরাং বক্ররেখা একমাত্রিক জ্যামিতির অন্তর্ভুক্ত।
তল
তল হলো একটি দ্বিমাত্রিক পৃষ্ঠ যা সমান (উঁচু নিচু নয় এমন) বা বক্র হতে পারে। যেমন বইয়ের একটি পৃষ্ঠা হলো একটি সমান তল বা সমতল; কিন্তু বইয়ের ঐ পাতাটি দিয়ে ঝালমুড়ি ওয়ালা যখন ঝালমুড়ির ঠোঙা তৈরি করে, তখন ঠোঙার তল হয় বক্রতল। আবার বৃত্ত ক্ষেত্রের তল হলো একটি সমতল। কিন্তু গোলক এর তল হল বক্রতল। অতএব তল হলো সমতলের সাধারণ রূপ। বিপরীতক্রমে, সমতল হলো তলের একটি বিশেষ রূপ।
ইউক্লিডিও জ্যামিতির মূল শাখা
জ্যামিতি যেহেতু পরিমাপের কাজে ব্যবহার করা হয়, তাই মাত্রা ও পরিমাপের ভিত্তিতে জ্যামিতিকে মোটামুটি দুইভাগে ভাগ করা যায়ঃ
- সমতল জ্যামিতি
- ঘন জ্যামিতি
সমতল জ্যামিতি
সমতল জ্যামিতি হলো দ্বিমাত্রিক জ্যামিতি।
সমতল জ্যামিতি মূলতঃ দ্বিমাত্রিক জ্যামিতিক চিত্রসমূহ নিয়েই গঠিত। এখানে বিন্দু, রেখা, কোণ, তল ইত্যাদি নিয়ে আলোচনা করা হয় এবং এদের দৈর্ঘ্য ও ক্ষেত্রফল পরিমাপ করা হয়।
গণিত শাস্ত্রে সমতল জ্যামিতি বলতে ইউক্লিডিও সমতল জ্যামিতিকে বুঝায়।
বিন্দু, রেখা, ত্রিভূজ, চতুর্ভুজ, বৃত্ত, উপবৃত্ত, অধিবৃত্ত, পরাবৃত্ত ইত্যাদি দ্বিমাত্রিক জ্যামিতিক চিত্রসমূহ সমতল জ্যামিতির অন্তর্গত। এইসব জ্যামিতিক চিত্রসমূহ এক টুকরা কাগজের উপর বা সমতলের উপর আঁকা যায়। এবং এদের অবস্থান, দৈর্ঘ্য, পরিসীমা ও ক্ষেত্রফল পরিমাপ করা হয়।
সমতল জ্যামিতি আবার হাই স্কুল জ্যামিতি নামে পরিচিত কারণ সারা দুনিয়ার হাই স্কুলে সমতল জ্যামিতি পড়ানো হয়।
ঘন জ্যামিতি
ঘন জ্যামিতি হলো ত্রিমাত্রিক জ্যামিতি। ত্রিমাত্রিক বলতে দৈর্ঘ্য, প্রস্থ ও উচ্চতা বা বেধকে বুঝায়। এখানে বিভিন্ন ধরনের ঘনবস্তু নিয়ে আলোচনা করা হয় এবং এদের আয়তন পরিমাপ করা হয়।
আয়তাকার ঘনবস্তু, ঘনক, কোণক, সিলিন্ডার, প্রিজম, পিরামিড, গোলক ইত্যাদি সবই ঘনবস্তু যা ত্রিমাত্রিক জগতে গঠিত হয়।

জগত বা ত্রিমাত্রিক জগৎ বা অসীম শুণ্য (Space)
জগত বলতে বুঝায় ত্রিমাত্রিক জগত যার মাত্রা তিনটি সীমাহীনভাবে বিস্তৃত। তাই জগত বা ফাঁকা স্থান বা অসীম শুণ্য হলো সমস্ত ত্রিমাত্রিক বিন্দুর সেট। অসীম শুণ্যের মধ্যে রয়েছে যেমন অসীম ত্রিমাত্রিক বিন্দু তেমনিভাবে রয়েছে অসীম সংখ্যক তল। এক কথায় বলা যায়, অসীম শুণ্য হলো অসীম ত্রিমাত্রিক বিস্তৃতি।
অতএব, জগতে বা স্পেসে বা ফাঁকা স্থানে বা শুণ্যে সব বস্তুরই একটি আপেক্ষিক অবস্থান রয়েছে। তেমনিভাবে সেখানে সব বস্তুরই একটি আপেক্ষিক দিকও রয়েছে।
ত্রিমাত্রিক জগতে যেকোনো বস্তুকেই বলা হয় ঘনবস্তু।
জ্যামিতিক মাত্রা কাকে বলে
জ্যামিতি বস্তুর আপেক্ষিক অবস্থান নিয়ে আলোচনা করে। জ্যামিতির প্রাথমিক ধারনা শিখতে প্রথমেই চলে আসে জ্যামিতিক মাত্রা কি? তাহলে জ্যামিতিক মাত্রা একটু আলোচনা করা যাকঃ
বিন্দু হলো শুণ্য মাত্রা (zero dimensional) বা মাত্রাবিহীন (no dimensional) জ্যামিতির অন্তর্গত। বিন্দু কেবল অবস্থান ছাড়া আর কিছুই নয়। এর কোন দৈর্ঘ্য, প্রস্থ, উচ্চতা বা বেধ নেই।
আবার একমাত্রিক (one dimensional) জ্যামিতি দুরত্ব সম্পর্কিত। অর্থাৎ দুরত্ব হলো একমাত্রিক জ্যামিতির অন্তর্ভুক্ত। এর শুধু দৈর্ঘ্য আছে। প্রস্থ, উচ্চতা বা বেধ নেই।
দ্বিমাত্রিক (two dimensional) জ্যামিতি ক্ষেত্রফলের সাথে সম্পৃক্ত। কারণ এর দৈর্ঘ্য ও প্রস্থ আছে।
ত্রিমাত্রিক (three dimensional) জ্যামিতি আয়তন -এর সাথে সম্পর্কিত। কারণ এর তিনটি মাত্রা- দৈর্ঘ্য, প্রস্থ ও উচ্চতা আছে।
বিভিন্ন মাত্রিক বস্তু গঠন প্রক্রিয়া
জ্যামিতি শেখার উপকারিতা
জ্যামিতি শেখার উপকারিতা অনেক। যেমন-
- বিশ্লেষণাত্মক চিন্তা: জ্যামিতি শেখার মাধ্যমে আমরা সমস্যা সমাধান করার দক্ষতা অর্জন করি।
- অ্যাবস্ট্রাক্ট থিঙ্কিং: জ্যামিতি আমাদের জটিল ধারণাগুলিকে সহজে বোঝার জন্য মস্তিষ্ককে প্রশিক্ষিত করে।
- প্রাকটিক্যাল অ্যাপ্লিকেশন: জীবনযাত্রার বিভিন্ন ক্ষেত্র যেমন স্থাপত্য, ডিজাইন, ইঞ্জিনিয়ারিংয়ে জ্যামিতি প্রয়োগ করা হয়।
জ্যামিতির ব্যবহার
জ্যামিতির ব্যবহার আমাদের জীবনে অনেক গুরুত্বপূর্ণ। এর কিছু ব্যবহার নিচে উল্লেখ করা হলো:
- নির্মাণ ও স্থাপত্য: ভবন, সেতু ও অন্যান্য কাঠামো নির্মাণের জন্য জ্যামিতির জ্ঞান অপরিহার্য।
- প্রকৌশল: বিভিন্ন ধরনের প্রকৌশল কাজে জ্যামিতির ব্যবহার রয়েছে।
- কম্পিউটার গ্রাফিক্স: কম্পিউটার গ্রাফিক্স ও গেম ডেভেলপমেন্টে জ্যামিতির ব্যবহার করা হয়। তাছাড়া, ডিজাইনের উপাদানগুলো উপযুক্ত অবস্থানে বসানো ক্ষেত্রে এটি ভূমিকা রাখে।
- মানচিত্র তৈরি: পৃথিবীর বিভিন্ন স্থানের মানচিত্র তৈরি করার জন্য জ্যামিতির প্রয়োজন।
- দৈনন্দিন জীবন: দৈনন্দিন জীবনে বিভিন্ন জিনিস পরিমাপ ও আকার বোঝার জন্য জ্যামিতির ধারণা গুরুত্বপূর্ণ।
- গাড়ি এবং বিমান নির্মাণ: রাস্তাঘাট, যানবাহন, এবং বিমানগুলোর ডিজাইনিংয়ের জন্যও জ্যামিতি অপরিহার্য।
- বিশ্বমানের গণনা: প্রযুক্তির ক্ষেত্রে জ্যামিতির সাহায্যে আমরা বিভিন্ন প্রযুক্তি, গ্রাফিক্স ডিজাইন, এবং কম্পিউটার অ্যানিমেশন করতে পারি।
- জ্যোতির্বিদ্যা: মহাকাশের জ্যামিতিক সম্পর্ক বুঝতে সাহায্য করে।
জ্যামিতি গাণিতিক ও বৈজ্ঞানিক অধ্যায়ের একটি অত্যন্ত গুরুত্বপূর্ণ শাখা। এটি আমাদের দৈনন্দিন জীবন থেকে শুরু করে বিভিন্ন পেশাগত ক্ষেত্রে অপরিহার্য ভূমিকা পালন করে। জ্যামিতি শেখা আমাদের চিন্তাভাবনা ও সমস্যা সমাধান ক্ষমতা বৃদ্ধি করে এবং আরও উন্নত বিশ্বের জন্য প্রস্তুত হতে সহায়তা করে।
জ্যামিতি আমাদের চারপাশের বিশ্বকে বুঝতে এবং বিভিন্ন সমস্যার সমাধান করতে সাহায্য করে। এটি আমাদের জীবনকে সহজ ও সুন্দর করে তোলে।
সমতলীয় জ্যামিতিক আকৃতি এর নাম ও তাদের চিত্রের তালিকা
রেখা
রেখা

বক্ররেখা
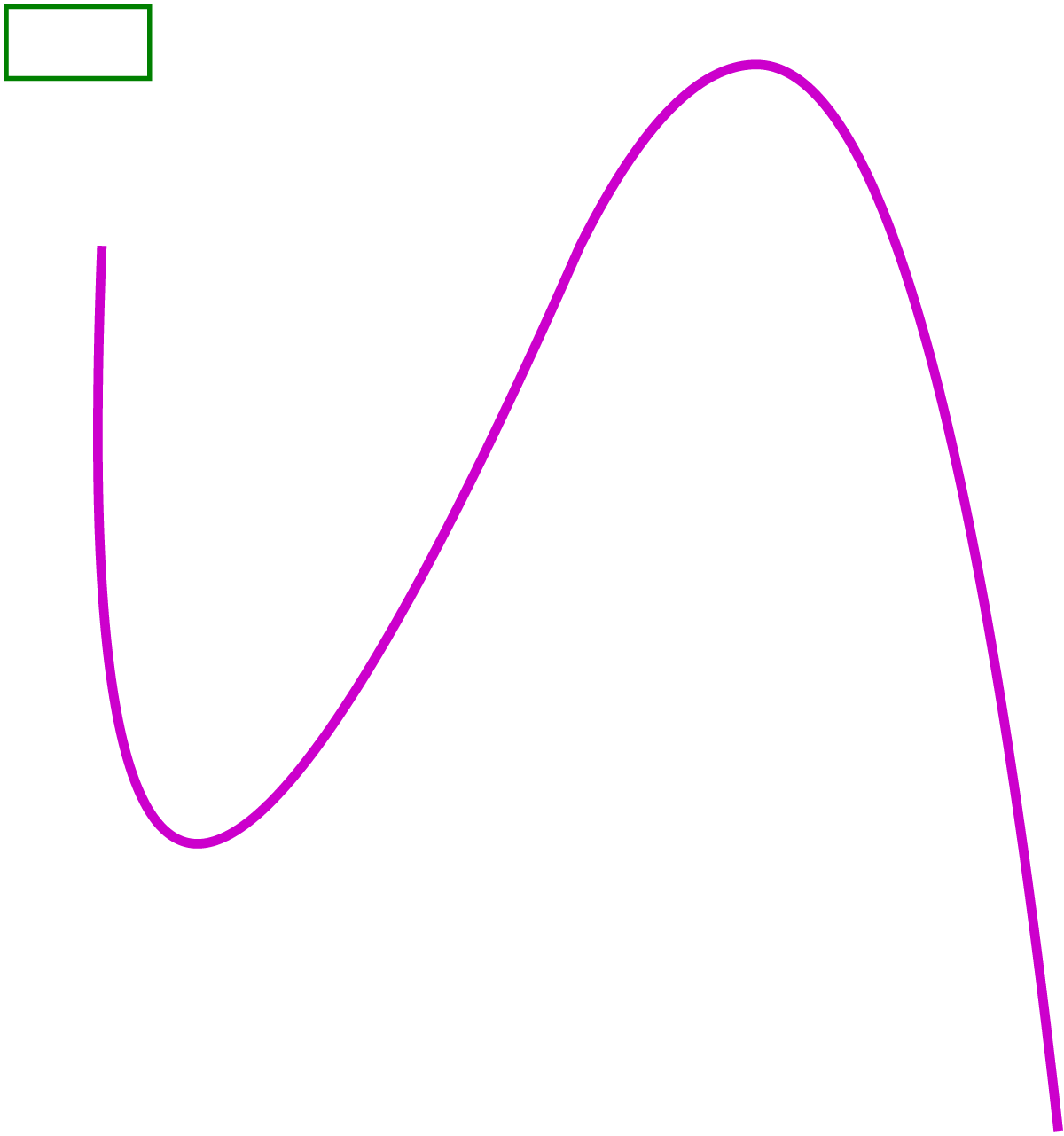
ত্রিভুজ
বিষমবাহু ত্রিভুজ

সমদ্বিবাহু ত্রিভুজ

সমবাহু ত্রিভুজ

সূক্ষ্মকোণী ত্রিভুজ
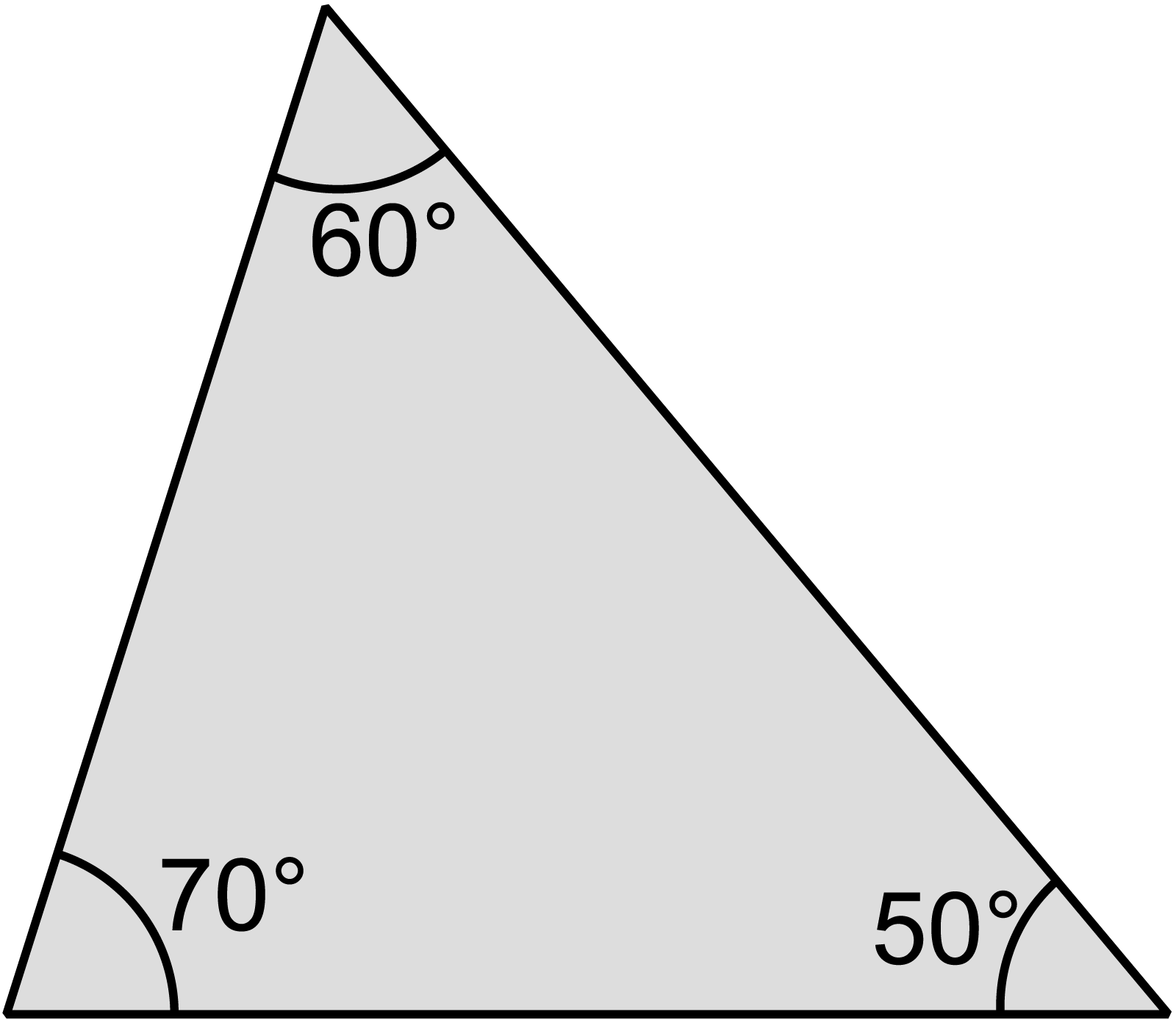
স্থুলকোণী ত্রিভুজ
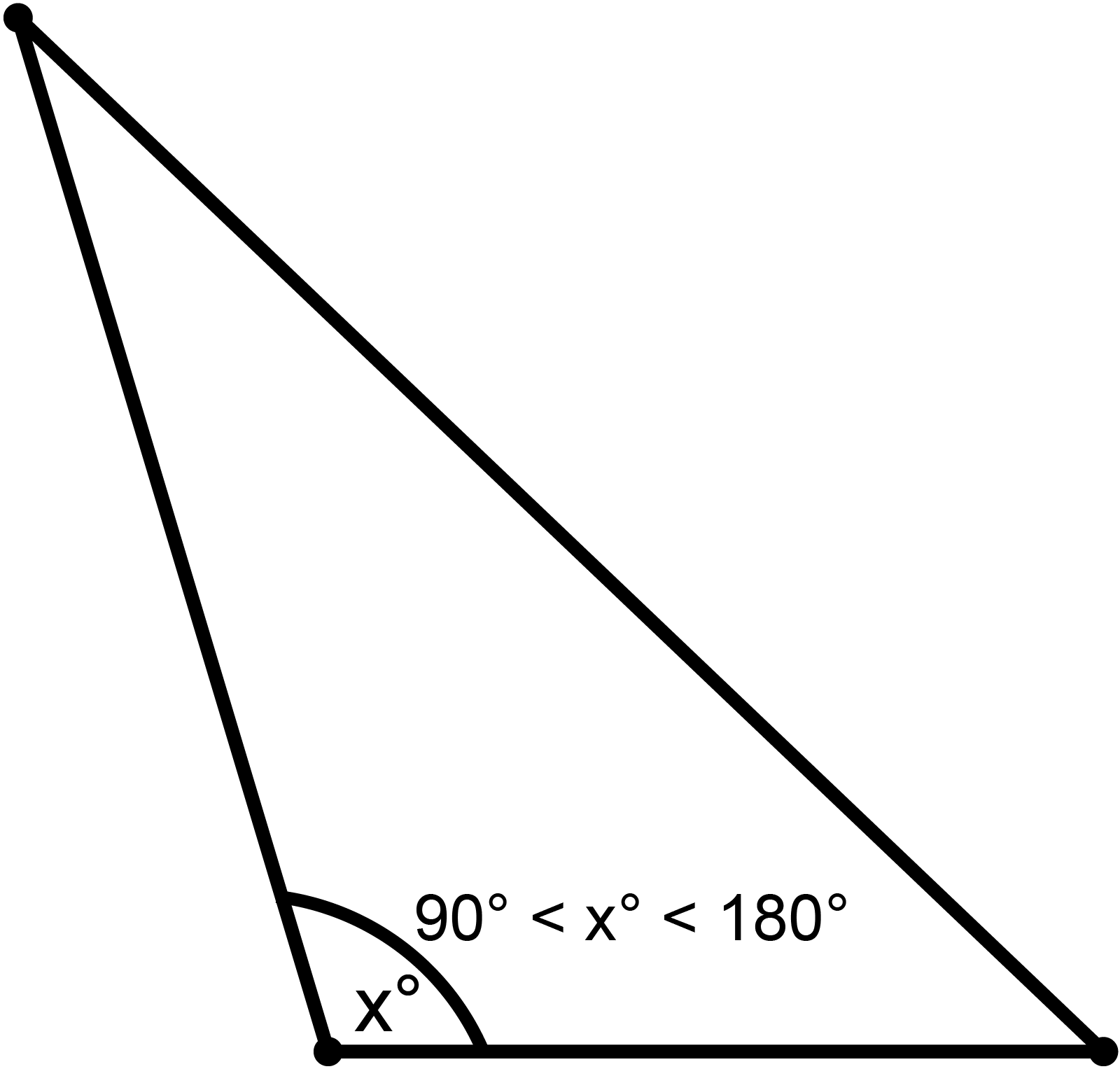
সমকোণী ত্রিভুজ
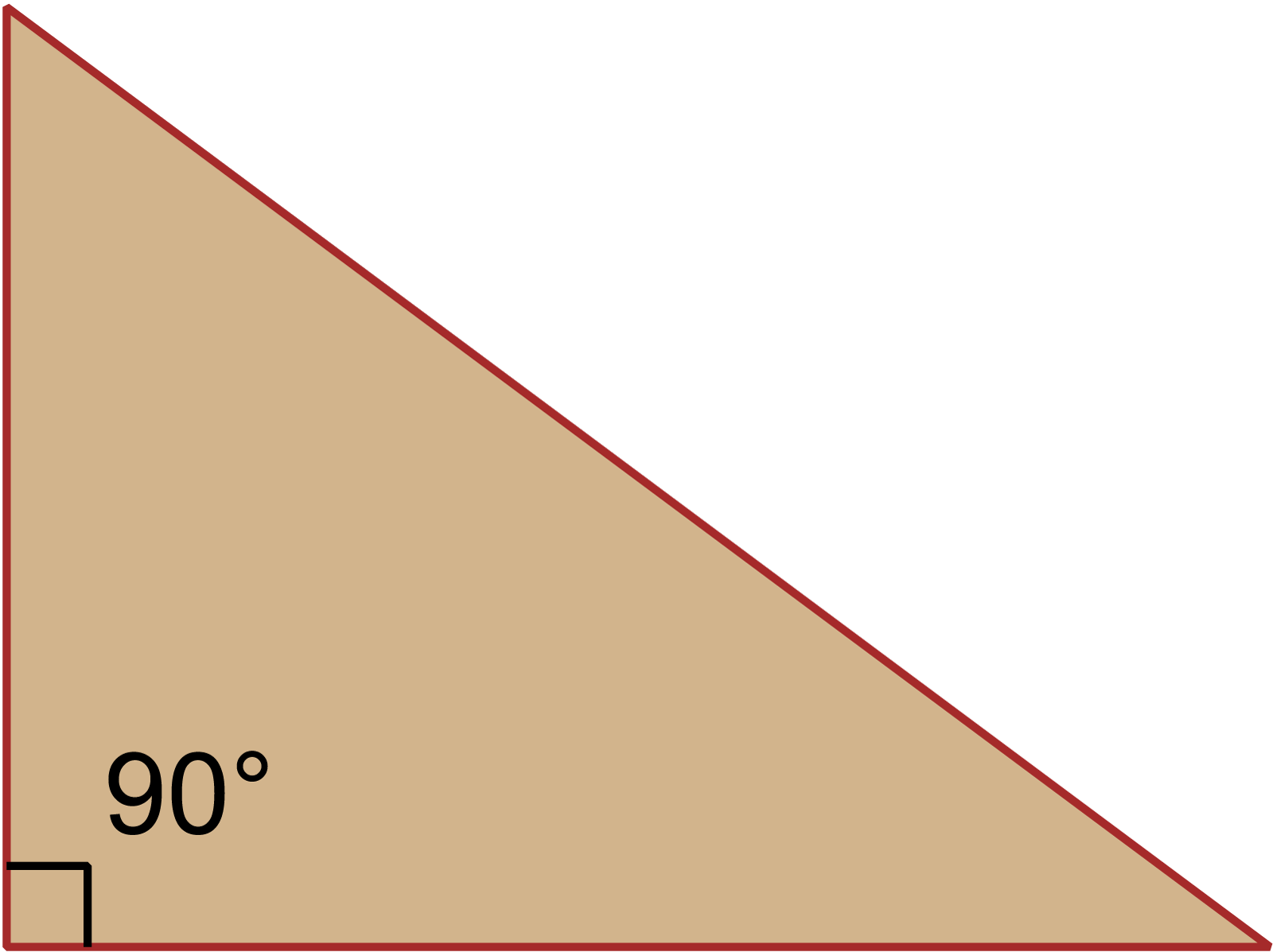
চতুর্ভুজ
চতুর্ভুজ

ট্রাপিজিয়াম
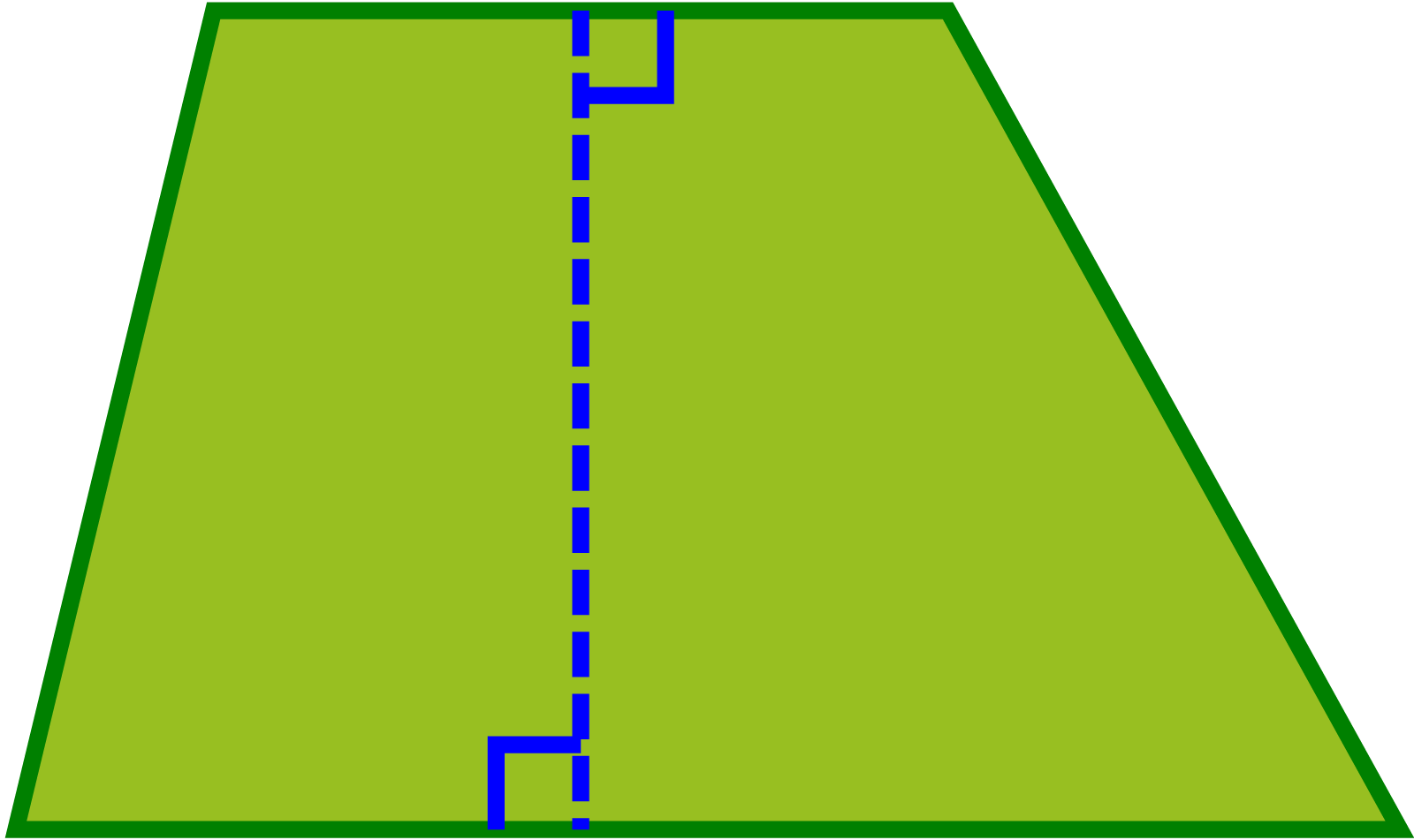
সমদ্বিবাহু ট্রাপিজিয়াম

সামান্তরিক

ঘুড়ি

রম্বস
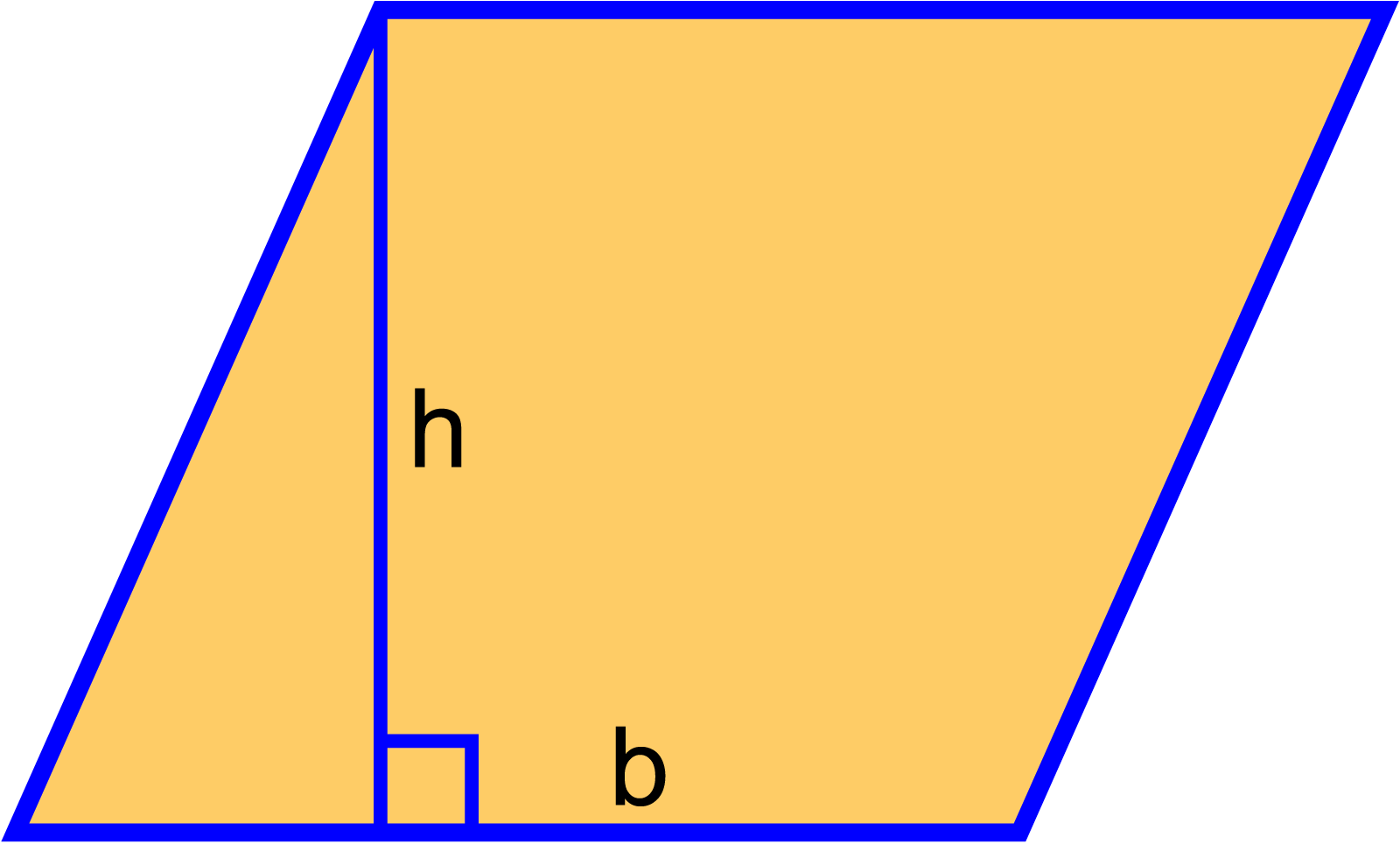
আয়ত

বর্গ
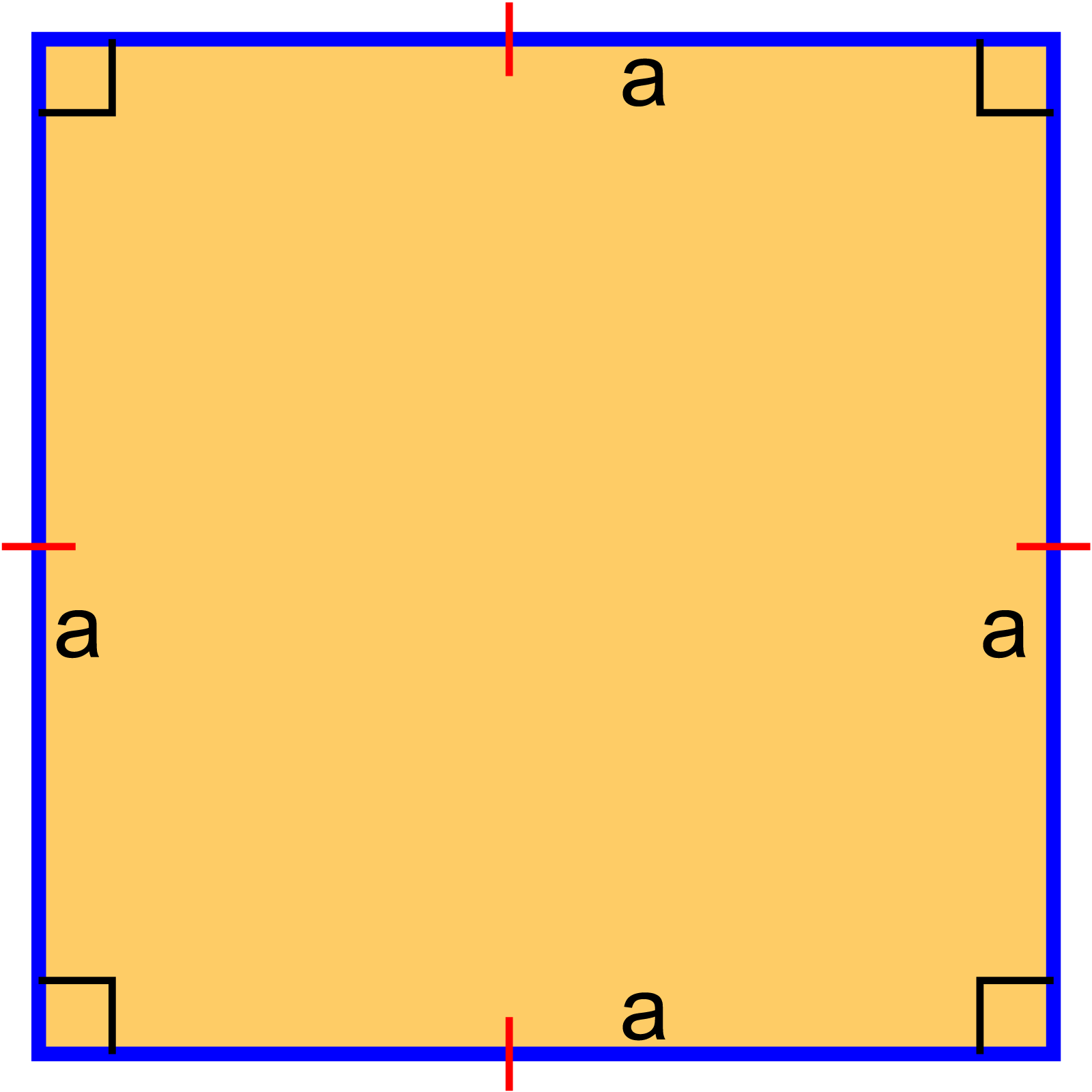
বহুভুজ
সমবাহু বহুভুজ

পঞ্চভুজ

ষষ্ঠভুজ

অষ্টভুজ

বৃত্ত
বৃত্ত
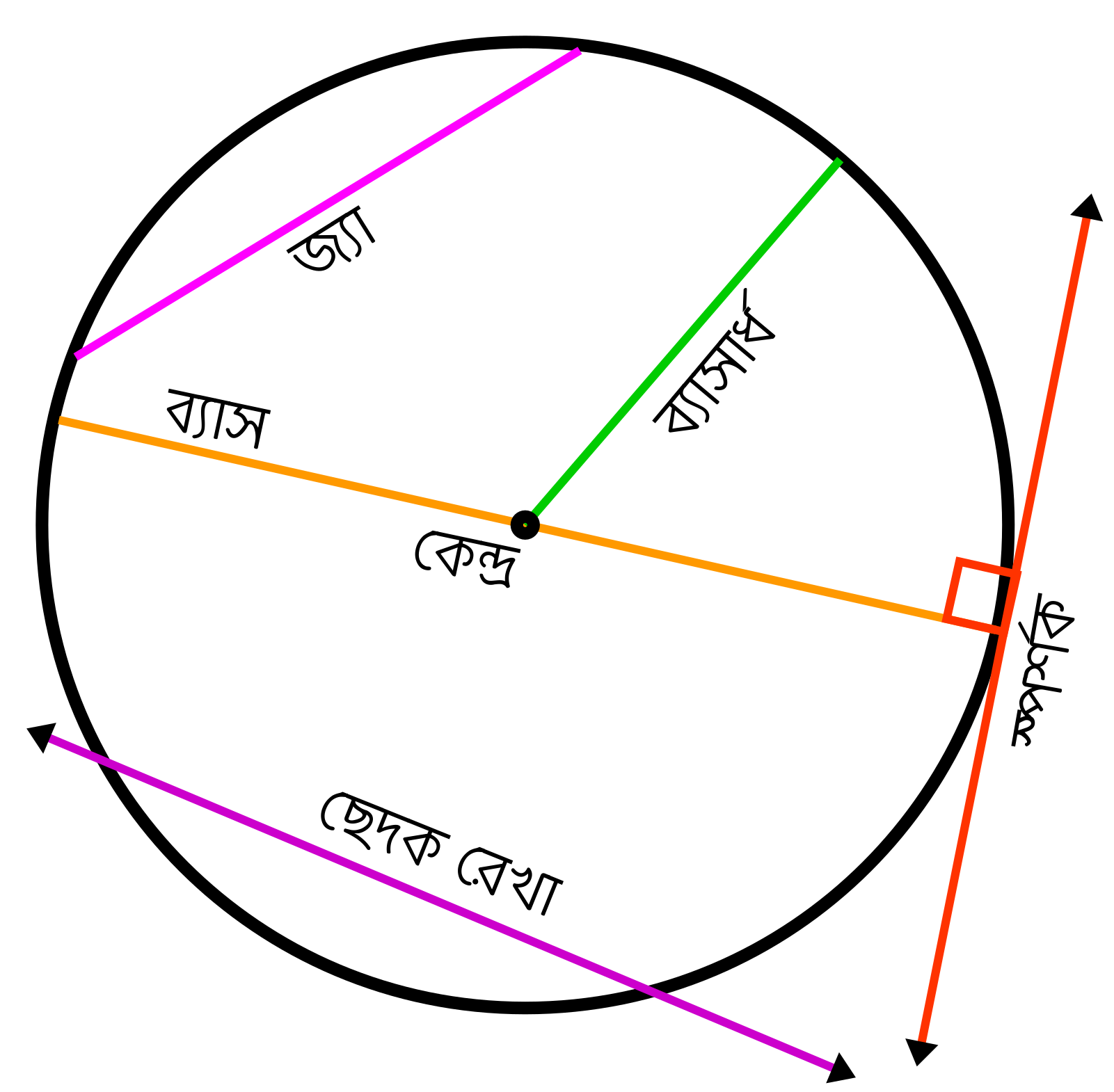
বৃত্তের ক্ষেত্রফল

কণিক সেকশন
উপবৃত্ত

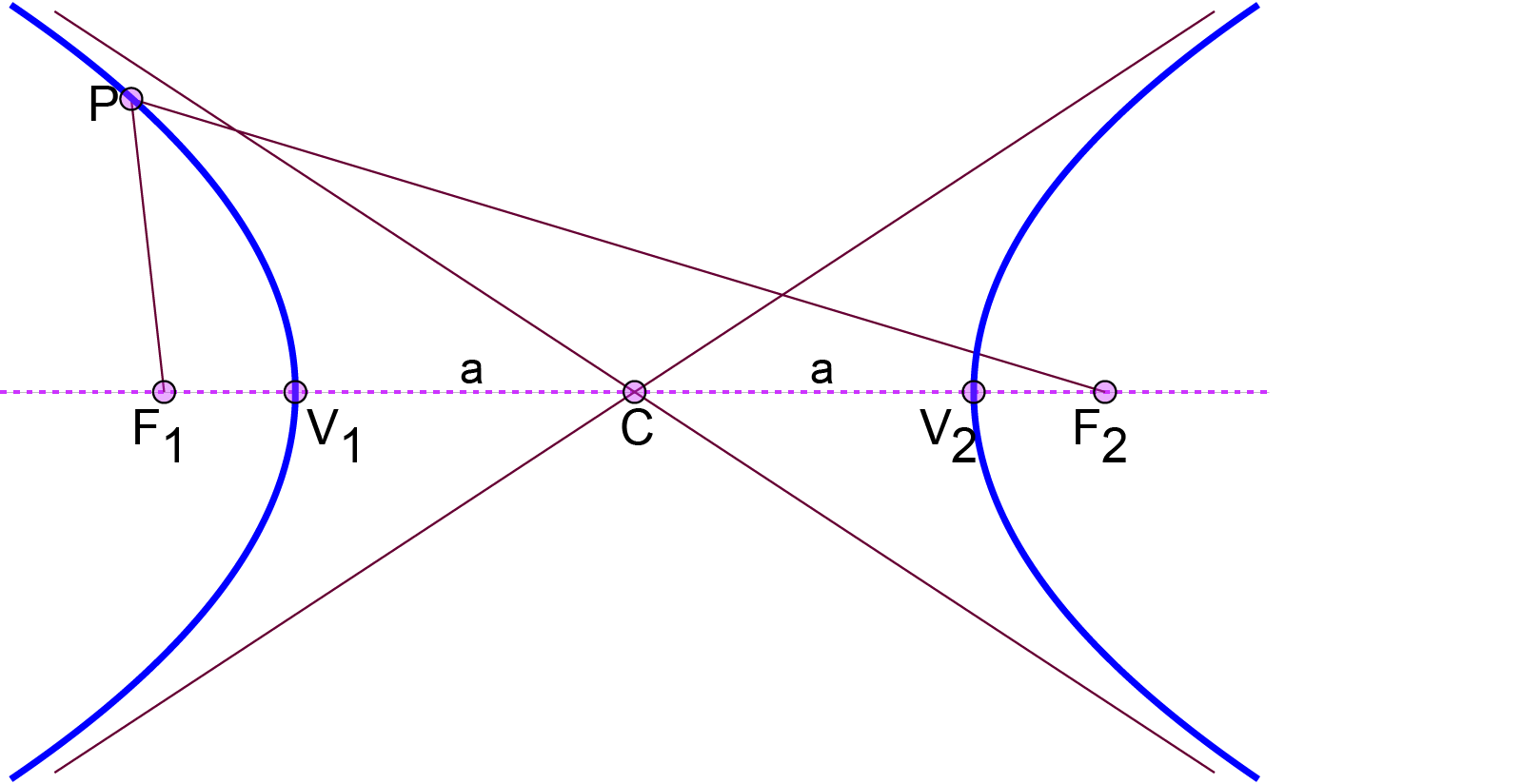
অধিবৃত্ত
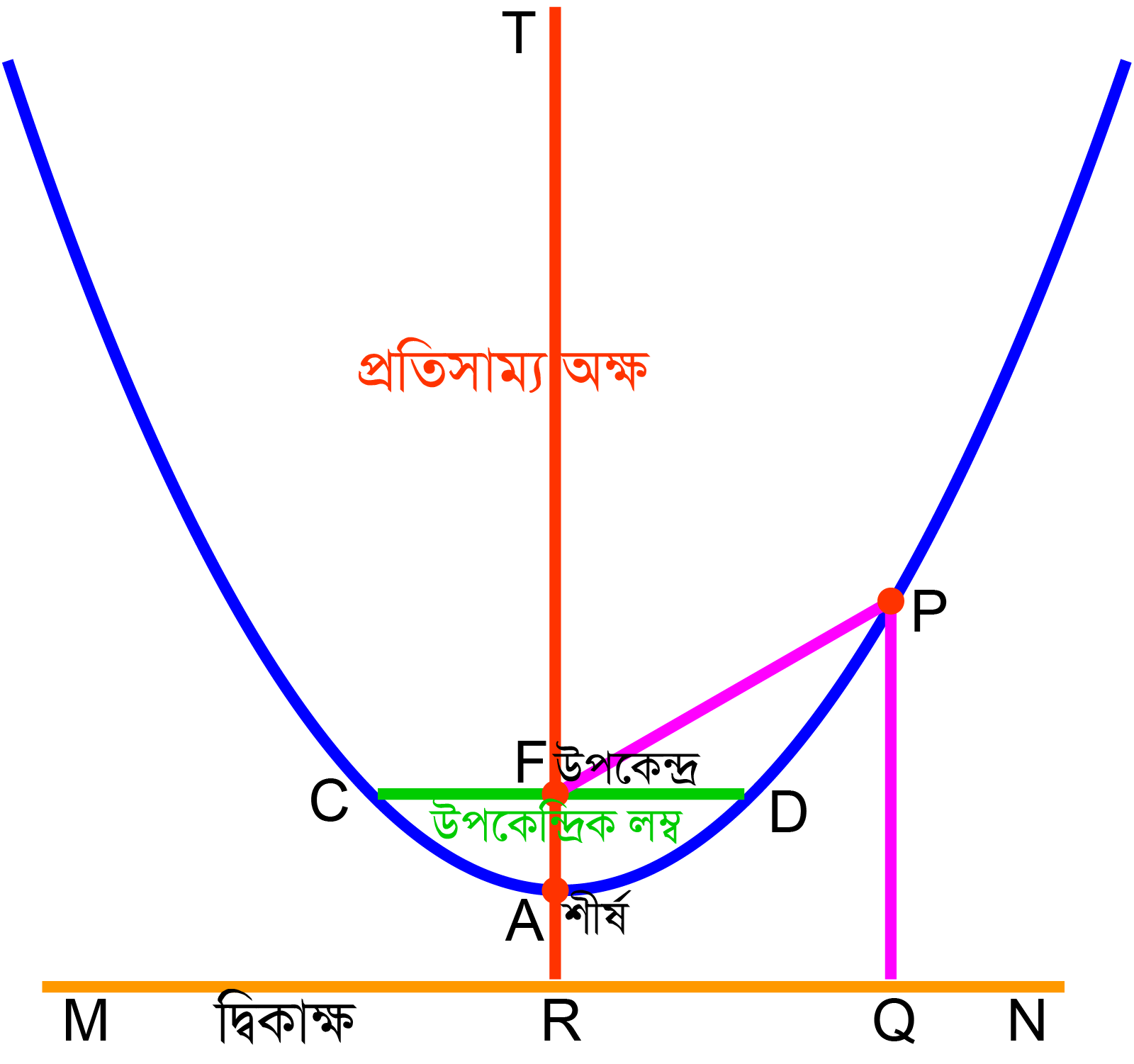
পরাবৃত্ত
ঘন জ্যামিতিক বস্তু ও চিত্র
ঘন জ্যামিতিক বস্তু
আয়তাকার ঘনবস্তু

ঘনক

সিলিন্ডার

কোণক

গোলক
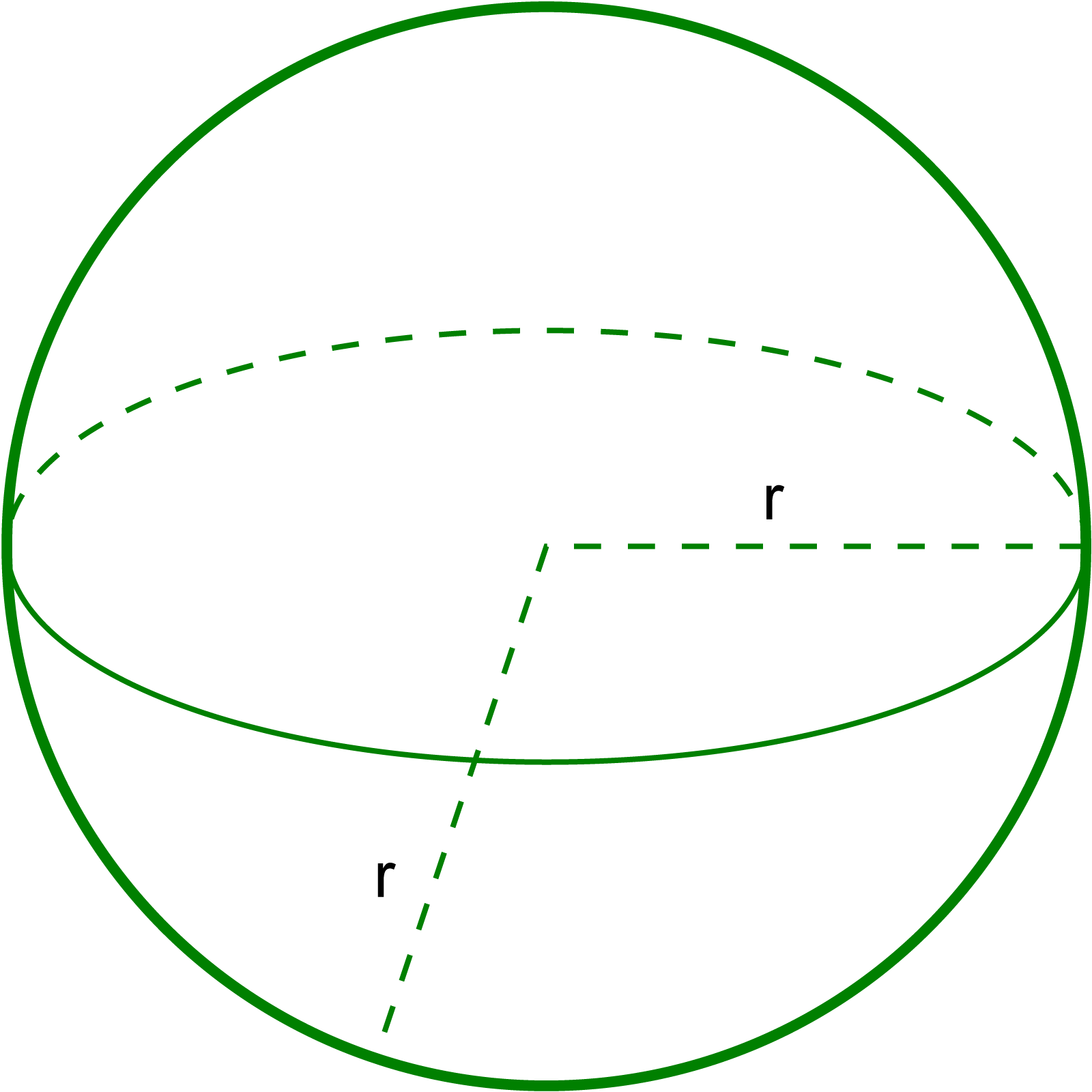
প্রিজম
পিরামিড
