রেখা কাকে বলে
এই টিউটোরিয়ালটির শেষে-
রেখা কাকে বলে তা ব্যাখ্যা করতে পারা যাবে।
রেখা কাকে বলে
যার অসীম দৈর্ঘ্য আছে কিন্তু, প্রস্থ ও বেধ নেই তাকে রেখা বলে।
অন্যভাবে বললে, একাধিক বিন্দু পরস্পর সংযোগের ফলে যে পথ তৈরি হয় তাকে রেখা বলে।
গণিত শাস্ত্রের কিংবদন্তি ইউক্লিড রেখাকে যেভাবে সংজ্ঞায়িত করেন, তা হলোঃ
”রেখা হলো প্রস্থহীন দৈর্ঘ্য“। তিনি আরও বলেছেন, এই প্রস্থহীন দৈর্ঘ্য তার উপর বিন্দুর সাপেক্ষে সমভাবে থাকে।
রেখার সবচেয়ে সহজবোধ্য সংজ্ঞাটি হলো নিম্নরূপ:
বিন্দু চলার পথকে রেখা বলে। তবে বিন্দু চলার এই পথটি সোজাও হতে পারে; আবার বাঁকাও হতে পারে। এ বিবেচনায় রেখাকে দুইভাবে ভাগ করা যায়।
- সরলরেখা
- বক্ররেখা
সরলরেখা
বিন্দু চলার পথটি সোজা হলে তাকে সরলরেখা বলে।
বক্ররেখা
বিন্দু চলার পথটি আঁকাবাঁকা হলে তাকে বক্ররেখা বলে।
তবে, আধুনিক গণিত শাস্ত্রে রেখা বলতে সরলরেখাকেই বুঝায়।

মনে করি, একটি রেখার উপর A ও B দুইটি ভিন্ন বিন্দু।
এটিকে পড়া হয় AB একটি রেখা এবং লিখে বুঝানো হয়।
আরেকভাবে রেখাকে সংজ্ঞায়িত করা যায় ...,
রেখা হলো প্রস্থ বা বেধহীন উভয়দিকে অসীম পর্যন্ত ক্রমবর্ধমান একটি সোজা (straight) দৈর্ঘ্য। যেহেতু রেখা উভয়দিক বরাবর সোজাসুজি অসীম পর্যন্ত বিরাজমান, তাই এর কোন প্রান্তবিন্দু নেই।
রেখার কেবল অসীম দৈর্ঘ্য আছে, এর কোন প্রস্থ বা বেধ নেই। তাই বলা যায়, রেখার কোনো নির্দিষ্ট দৈর্ঘ্য নেই। কিন্তু রেখাংশের নির্দিষ্ট দৈর্ঘ্য আছে। রেখা শুধু দৈর্ঘ্য সংশ্লিষ্ট হওয়ার কারণে, রেখা এক-মাত্রিক জ্যামিতির অন্তর্ভূক্ত।
অসীম দৈর্ঘ্য বলতে বুঝায়, রেখার দৈর্ঘ্য উভয়দিকে অসীম পর্যন্ত ক্রমবর্ধমান। তাই, রেখার কোনো নির্দিষ্ট দৈর্ঘ্য নেই। রেখার কোনো প্রান্ত বিন্দু নেই বলে, রেখাকে ইচ্ছামত উভয় দিক বরাবর বাড়ানো যায়।
আবার, স্থানাঙ্ক জ্যামিতির সাহায্যে রেখাকে সংজ্ঞায়িত করলে দাঁড়ায়,
একটি রেখা হলো কতকগুলো বিন্দুর সেট যে বিন্দুগুলো উভয়দিকে একদম সোজা বরাবর অসীম পর্যন্ত বিস্তৃত।
আবার, সমতলের ধারণা থেকে রেখার ধারণা লাভ করা যায়। উদাহরণস্বরূপ বলা যায়.., বইয়ের একটি পৃষ্ঠার দৈর্ঘ্যকে স্থির রেখে প্রস্থকে ক্রমশ হ্রাস করতে করতে অবশেষে শুণ্যে পরিণত করলে একটি মাত্র রেখা অবশিষ্ট থাকে। এভাবে তলের ধারণা থেকে রেখার ধারণা পাওয়া যায়।
নানা ধরণের জ্যামিতিক আকার ও আকৃতি রেখার সাহায্যে তৈরি করা যায়। যেমন- সরলরেখা ব্যবহার করে ত্রিভুজ, চতুর্ভুজ, ট্রাপিজিয়াম, বর্গক্ষেত্র, ঘুড়ি ও সকল প্রকার বহুভূজ তৈরি করা যায়।
আবার, বক্ররেখা ব্যবহার করে বৃত্ত, পরাবৃত্ত, অধিবৃত্ত, উপবৃত্ত ইত্যাদি জ্যামিতিক আকার-আকৃতিগুলো তৈরি করা যায়।
সরলরেখার উদাহরণ

একটি রেখার মধ্যে নিম্নলিখিত বিষয় দুইটি অন্তর্ভূক্ত।
- রেখাংশ
- রশ্মি
যদিও রেখাংশ ও রশ্মি সম্বন্ধে পরিপূর্ণ জ্ঞানলাভের জন্য অন্য দুইটি টিউটোরিয়ালের মাধ্যমে রেখাংশ এবং রশ্মি সম্পর্কে বিশদভাবে আলোচনা করা হওয়ছে, তবুও এখানে বিষয় দুইটি সম্পর্কে একটু জেনে নেওয়া যাক।
রেখাংশ
রেখাংশ হলো রেখার একটি সসীম অংশ। তাই রেখাংশের দুইটি প্রান্তবিন্দু থাকে। এর প্রান্তবিন্দুদ্বয়ের মাঝের সকল বিন্দু রেখাংশের উপর অবস্থিত।

রশ্মি
রশ্মি হলো রেখার একটি অংশ যা একটি প্রান্তবিন্দু থেকে শুরু হয়ে অসীম পর্যন্ত চলতে থাকে।

দুইটি জানা বিন্দু থেকে সরলরেখা অঙ্কনের অ্যাপস। যেকোনো দুইটি বিন্দু লিখে রেখা আঁকি বাটনে ক্লিক করলে সরলরেখাটি অঙ্কিত হয়। তাছাড়া, রেখাটির তীর চিহ্ন গ্রাফের ধারের যে বিন্দুতে ছেদ করে এটি সেই স্থানাঙ্কও প্রদর্শন করে।
দুইটি জানা বিন্দু থেকে সরলরেখা অঙ্কনের এ্যাপ
x1= y1= x2= y2=
রেখাটি গ্রাফের যে প্রান্তবিন্দুতে ছেদ করে
x1= y1= x2= y2=রেখার ঢাল কি
একটি রেখার উপর দুইটি ভিন্ন বিন্দুর y স্থানাঙ্কের পরিবর্তনকে x স্থানাঙ্কের পরিবর্তন দ্বারা ভাগ করলে রেখাটির ঢাল পাওয়া যায়। সুতরাং, কোন সরলরেখার ঢাল একটি সংখ্যা। এই সংখ্যাটি ধনাত্নক বা ঋনাত্নক হতে পারে। আবার শুণ্যও হতে পারে। ঢালকে m দ্বারা সূচিত করা হয়।
মনেকরি, একটি রেখার উপর P(x1,y1) এবং Q(x2,y2) দুইটি ভিন্ন বিন্দু যেখানে x1 ≠ x2.
সুতরাং ঢাল,
m = y স্থানাঙ্কের পার্থক্যx স্থানাঙ্কের পার্থক্য
বা, m = y2 - y1x2 - x1
বা, m = ΔyΔx
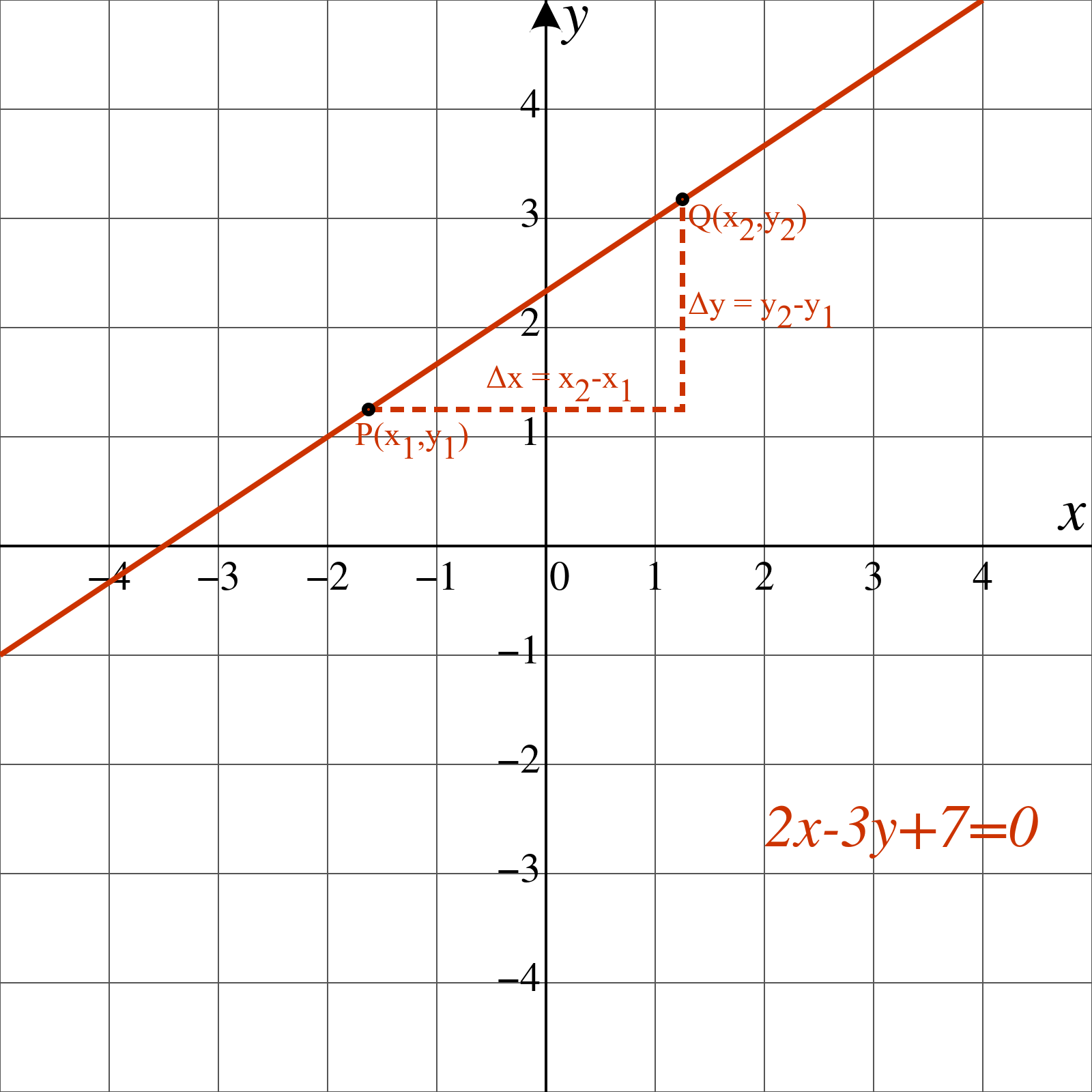
P(x1,y1) এবং Q(x2,y2) যেখানে x1 ≠ x2; বিন্দু দুইটি দিয়ে গমনকারী সরলরেখার ঢাল
m = y2 - y1x2 - x1
মনেকরি, একটি সরলরেখার সমীকরণ 3x + 2y = 7 এবং P(-3,8) ও Q(-5,11) সরলরেখাটির উপর দুইটি বিন্দু।
সুতরাং PQ সরলরেখাটির ঢাল,
m = y2 - y1x2 - x1
বা, m = 11-8-5 - (-3)
বা, m = 3-5 + 3
বা, m = 3-2
∴ m = - 32
সরলরেখার সমীকরণ
প্রদত্ত তথ্যের উপর ভিত্তি করে সরল রেখার সমীকরণ নির্ণয় করা যায়। বিন্দু, ঢাল, অক্ষদ্বয়ের ছেদক অংশ ইত্যাদির উপর নির্ভর করে সরলরেখার সমীকরণ গঠন যায়। সাধারণত যেসব নুন্যতম তথ্যের উপর ভিত্তি করে সরল রেখার সমীকরণ গঠন করা যায় তা নিচে দেওয়া হলো।
- ঢাল ও একটি নির্দিষ্ট বিন্দু দিয়ে যায়
- ঢাল ও যেকোন অক্ষের ছেদক
- দুইটি নির্দিষ্ট বিন্দু দিয়ে গমনকারী
- অক্ষদ্বয়ের ছেদকাংশ
ঢাল ও একটি নির্দিষ্ট বিন্দু দিয়ে গমনকারী সরলরেখার সমীকরণ এর সূত্র উদ্ভাবন
প্রথম পদ্বতি
P(x1,y1) এবং Q(x2,y2) বিন্দুগামী সরলরেখার ঢাল
m = y2 - y1x2 - x1
যেখানে x1 ≠ x2;
এখন P(x1,y1) যদি একটি নির্দিষ্ট বিন্দু এবং Q একটি চলক বিন্দু যেখানে Q(x,y) হয় অর্থাৎ, Q(x2,y2) = Q(x,y) হয়, তাহলে ঢাল দাঁড়ায়,
m = y2 - y1x2 - x1
বা, m = y - y1x - x1
∴ y - y1 = m(x - x1)
এটিই নির্ণেয় সরলরেখার সমীকরণ।
যেখানে x ≠ x1; কারণ x = x1 হলে তখন আর এটি সরলরেখা থাকে না; এটি তখন একটি বিন্দু হয়ে যায়।
দ্বিতীয় পদ্বতি
আবার (x1,y1) এবং (x2,y2) বিন্দুদ্বয় দিয়ে অতিক্রান্ত সরলরেখার ঢাল
m = y2 - y1x2 - x1
যেখানে x1 ≠ x2; এবং সরলরেখার সমীকরণটি
y - y1y2 - y1 = x - x1x2 - x1
বা, y - y1x - x1 = y2 - y1x2 - x1
বা, y - y1x - x1 = m
∴ y - y1 = m(x - x1)
এটিই নির্ণেয় সরল রেখার সমীকরণ।

m ঢাল বিশিষ্ট এবং (x1, y1) বিন্দুগামী সরলরেখার সমীকরণ
y - y1 = m(x - x1)
ঢাল ও যেকোন অক্ষের ছেদকাংশ এর ভিত্তিতে সরলরেখার সমীকরণ এর সূত্র উদ্ভাবন
কোন সরলরেখার ঢাল এবং রেখাটি দ্বারা x-অক্ষ বা y-অক্ষের কতটুকু অংশ কর্তন হয় তার উপর ভিত্তি করে সরলরেখার সমীকরণ নির্ণয় করা যায়। সরলরেখাটি দ্বারা অক্ষদ্বয়ের যতটুকু অংশ কাটা পড়ে, ততটুকু পরিমানকে সংশ্লিষ্ট অক্ষের ছেদকাংশ বলা হয়। আরও সুস্পষ্ট করে বলা যায়, সরলরেখাটি কোন অক্ষকে যে বিন্দুতে ছেদ করে, মূলবিন্দু (0,0) থেকে সেই বিন্দুর দুরত্বকে উক্ত অক্ষের ছেদক বলে।
ঢাল ও অক্ষের ছেদকের ভিত্তিতে দুইভাবে সরলরেখার সমীকরণ গঠন করা যায়।
- ঢাল ও y-অক্ষের ছেদকের ভিত্তিতে সরলরেখার সমীকরণ
- ঢাল ও x-অক্ষের ছেদকের ভিত্তিতে সরলরেখার সমীকরণ
ঢাল ও y-অক্ষের ছেদকের ভিত্তিতে সরলরেখার সমীকরণ এর সূত্র উদ্ভাবন
মনেকরি, সরলরেখাটির ঢাল m এবং y-অক্ষের ছেদক c অর্থাৎ রেখাটি y অক্ষকে (0,c) বিন্দুতে ছেদ করে।
ইতোমধ্যে শেখা হয়েছে, m ঢাল বিশিষ্ট এবং (x1,y1) বিন্দুগামী সরলরেখার সমীকরণ
y - y1 = m(x - x1)
উপরোক্ত সরলরেখাটি (0,c) বিন্দু দিয়ে যায়। ফলে,
c - y1 = m(0 - x1)
বা, c - y1 = m(- x1)
বা, c - y1 = -mx1
বা, c + mx1 = y1
∴ y1 = c + mx1
y1 এর মান মূল সমীকরণটিতে বসাই,
y - y1= m(x - x1)
বা, y - (c + mx1) = m(x - x1)
বা, y - c - mx1 = mx - mx1
বা, y = mx - mx1 + c + mx1
∴ y = mx + c
এটিই নির্ণেয় সরলরেখার সমীকরণ।

কোন সরলরেখার ঢাল m এবং y-অক্ষের ছেদক c হলে সরলরেখাটির সমীকরণ
y = mx + c
ঢাল ও x-অক্ষের ছেদকের ভিত্তিতে সরলরেখার সমীকরণ এর সূত্র উদ্ভাবন
মনেকরি, সরলরেখাটির ঢাল m এবং x-অক্ষের ছেদক b অর্থাৎ, রেখাটি x অক্ষকে (b,0) বিন্দুতে ছেদ করে।
এই টিউটোরিয়ালটিতে উপরে দেখানো হয়েছে, কোন রেখার ঢাল m এবং (x1, y1) বিন্দু দিয়ে অতিক্রান্ত সরলরেখার সমীকরণ
y - y1 = m(x - x1)
উপরোক্ত সরলরেখাটি (b,0) বিন্দু দিয়ে যায়। ফলে,
0 - y1 = m(b - x1)
বা, 0- y1 = m(b - x1)
বা, - y1 = bm - mx1
বা, - y1 = -(-bm + mx1)
∴ y1 = mx1 - bm
y1 এর মান মূল সমীকরণটিতে বসাই,
y - y1 = m(x - x1)
বা, y - (mx1 - bm) = m(x - x1)
বা, y - mx1 + bm = mx - mx1
বা, y = mx - mx1 + mx1 - bm
বা, y = mx - bm
বা, y = m(x - b)
বা, m(x - b) = y
বা, x - b = 1m y
বা, x = 1m y + b
বা, x = ny + b
যেখানে n = 1m অর্থাৎ, mn=1.
এটিই নির্ণেয় সরলরেখার সমীকরণ।
কোন সরলরেখার ঢাল m এবং x-অক্ষের ছেদক b হলে সরলরেখাটির সমীকরণ
x = ny + b
যেখানে n = 1m অর্থাৎ, mn = 1.
দুইটি নির্দিষ্ট বিন্দু দিয়ে গমনকারী সরলরেখার সমীকরণ এর সূত্র উদ্ভাবন
কোন সরল রেখার দুইটি নির্দিষ্ট বিন্দু দেওয়া থাকলে তার সমীকরণ নির্ণয় করা যায়। মনেকরি, কোন সরলরেখার উপর (x1, y1) ও (x2, y2) দুইটি নির্দিষ্ট বিন্দু। এই রেখাটির সমীকরণ নির্ণয় করতে হবে।
আবার, মনেকরি রেখাটির ঢাল m. আগেই শেখা হয়েছে m ঢাল বিশিষ্ট (x1, y1) বিন্দুগামী সরলরেখার সমীকরণ
y - y1 = m(x - x1)
এই রেখাটি (x2, y2) বিন্দু দিয়ে যায়। তাই,
y2 - y1 = m(x2 - x1)
বা, m(x2 - x1) = y2 - y1
∴ m = y2 - y1x2 - x1
এখন m এর মান মূল সমীকরণটিতে বসাই,
y - y1 = m(x - x1)
বা, y - y1 = y2 - y1x2 - x1 (x - x1)
∴ y - y1y2 - y1 = x - x1x2 - x1
এটিই নির্ণেয় সরলরেখার সমীকরণ।
দুইটি নির্দিষ্ট বিন্দু (x1, y1) এবং (x2, y2) দিয়ে গমনকারী সরলরেখার সমীকরণ
y - y1y2 - y1 = x - x1x2 - x1
উভয় অক্ষের ছেদকাংশ এর ভিত্তিতে সরলরেখার সমীকরণ এর সূত্র উদ্ভাবন
কোন সরলরেখা x-অক্ষ এবং y-অক্ষকে কতটুকু অংশ কাটে, তার উপর নির্ভর করে সরল রেখার সমীকরণ নির্ণয় করা যায়। সরলরেখাটি x-অক্ষকে যে বিন্দুতে ছেদ করে মূলবিন্দু (0,0) থেকে সেই বিন্দুর দুরত্বকে x অক্ষের ছেদকাংশ বলে। আবার রেখাটি y-অক্ষকে যে বিন্দুতে ছেদ করে মূলবিন্দু (0,0) থেকে সেই বিন্দুর দুরত্বকে y অক্ষের ছেদকাংশ বলে।
মনেকরি, সরলরেখাটি দ্বারা x-অক্ষ এবং y-অক্ষের ছেদকাংশ যথাক্রমে a এবং b. অর্থাৎ, রেখাটি x-অক্ষকে P(a,0) বিন্দুতে ও y-অক্ষকে Q(0,b) বিন্দুতে ছেদ করে যেখানে a≠ 0, b≠ 0; এবং রেখাটির ঢাল m.
জানা আছে, (x1, y1) বিন্দু দিয়ে অতিক্রান্ত এবং m বিশিষ্ট রেখার সমীকরণ
y - y1 = m(x - x1)
সুতরাং, (a,0) বিন্দু দিয়ে অতিক্রান্ত এবং m বিশিষ্ট রেখার সমীকরণ
y - y1 = m(x - x1)
বা, y - 0 = m(x - a)
বা, y = m(x - a)
এই রেখাটি (0,b) বিন্দু দিয়ে অতিক্রম করে।
b = m(0 - a)
বা, b = m(- a)
বা, b = -ma
বা, -ma = b
∴ m = - ba
এখন মূল সমীকরণটি লিখি এবং m এর মান বসাই,
y = m(x - a)
বা, y = - ba (x - a)
বা, y = - bxa + b
বা, bxa + y = b
উভয় পক্ষকে b দ্বারা ভাগ করি,
বা, bxab + yb = 1
∴ xa + yb = 1
এটিই নির্ণেয় সরলরেখার আদর্শ সমীকরণ।
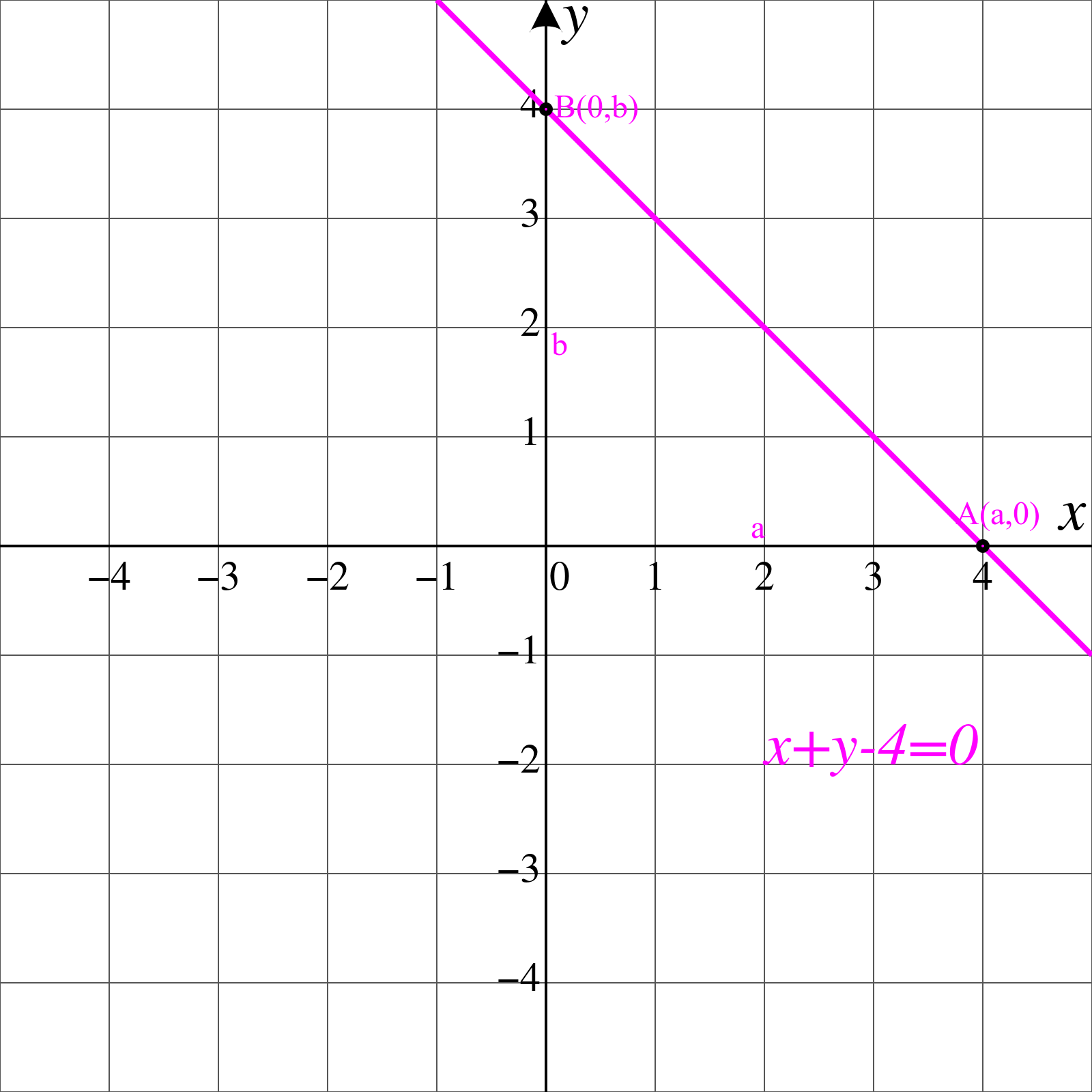
কোন সরলরেখার x-অক্ষ এবং y-অক্ষের ছেদকাংশ যথাক্রমে a ও b যেখানে a≠ 0, b≠ 0 হলে; সরল রেখাটির সমীকরণ
xa + yb = 1