সমকোণী ত্রিভুজের পরিসীমা ও সমকোণী ত্রিভুজের পরিসীমার সূত্র

সমকোণী ত্রিভুজের পরিসীমা বলতে সমকোণী ত্রিভুজের বাহু তিনটির সমষ্টিকে বুঝায়। সমকোণী ত্রিভুজের বাহুগুলো হলো লম্ব, ভূমি ও অতিভুজ। কাজেই এই বাহগুলোর যোগফলই হলো সমকোণী ত্রিভুজের পরিসীমা।

অতএব, সমকোণী ত্রিভুজের লম্ব, ভূমি ও অতিভূজের সমষ্টিকে সমকোণী ত্রিভুজের পরিসীমা বলে। আবার অন্যভাবে সমকোণী ত্রিভুজের পরিসীমাকে সংজ্ঞায়িত করা যায়।

সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটি ও অতিভুজের সমষ্টিকে সমকোণী ত্রিভুজের পরিসীমা বলে।

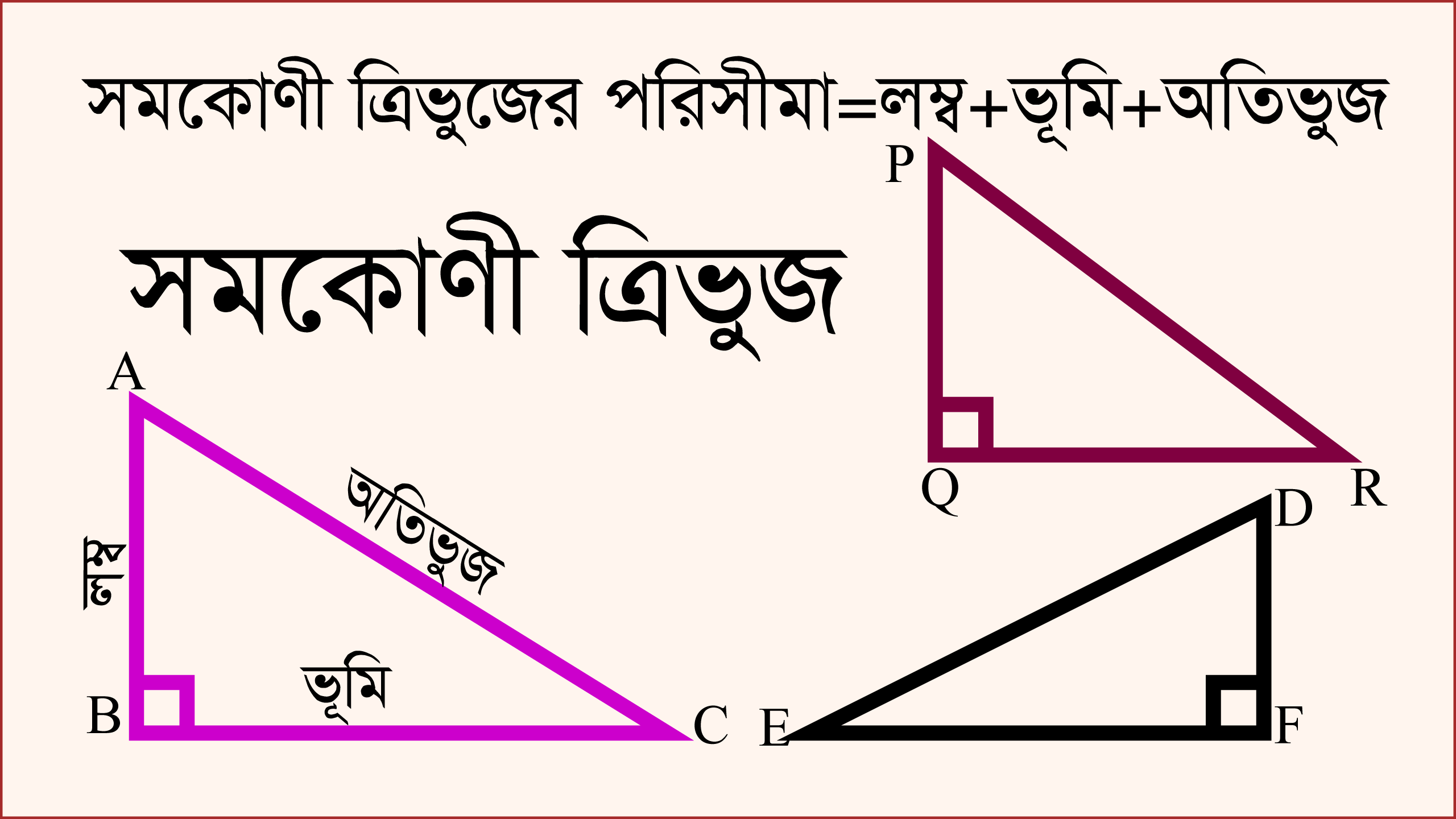
তাহলে পরিসীমা নির্ণয়ের জন্য বাহু তিনটিকে চেনা যাক। সমকোণ সংলগ্ন বাহু দুইটিকে ভূমি ও লম্ব বলে। অর্থাৎ, সমকোণ সংলগ্ন বাহুদ্বয়ের যেকোনো একটি ভূমি হলে অপরটিকে লম্ব বলে। আর সমকোণের বিপরীত বাহুটিকে অতিভুজ বলে।

সমকোণী ত্রিভুজের পরিসীমার সূত্র

যে সূত্রের সাহায্যে সমকোণী ত্রিভুজের পরিসীমা নির্ণয় করা হয় তাকে সমকোণী ত্রিভুজের পরিসীমার সূত্র বলে। যেহেতু সমকোণী ত্রিভুজের পরিসীমা হলো এর বাহুগুলোর দৈর্ঘ্যের সমষ্টি, তাহলে সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র দাঁড়ায়,
পরিসীমা = (লম্ব + ভূমি + অতিভূজ) একক।

∴ সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র = (লম্ব + ভূমি + অতিভূজ) একক।

একটি সমকোণী ত্রিভুজের লম্ব a একক, ভূমি b একক, অতিভুজ c একক এবং পরিসীমা P একক হলে,

সমকোণী ত্রিভুজের পরিসীমার সূত্র = (a + b + c) একক। অর্থাৎ,

P = (a + b + c) একক।

সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র

সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র নির্ণয়ের আগে সমকোণী সমদ্বিবাহু ত্রিভুজ কাকে বলে তা জানা দরকার। যে ত্রিভুজ একইসাথে সমদ্বিবাহু ও সমকোণী, তাই সমকোণী সমদ্বিবাহু ত্রিভুজ।

যেহেতু ত্রিভুজটি সমকোণী, এর সমকোণের বিপরীত বাহুটি হলো অতিভুজ।

আবার যেহেতু ত্রিভুটি সমদ্বিবাহু, তাই এর দুইটি বাহু পরস্পর সমান। তাহলে অতিভুজ ব্যতীত এর অপর দুইটি বাহু হলো ভূমি ও লম্ব। কাজেই, সমকোণী সমদ্বিবাহু ত্রিভুজের ভূমি ও লম্ব পরস্পর সমান।

∴ ভূমির দৈর্ঘ্য = লম্বের দৈর্ঘ্য

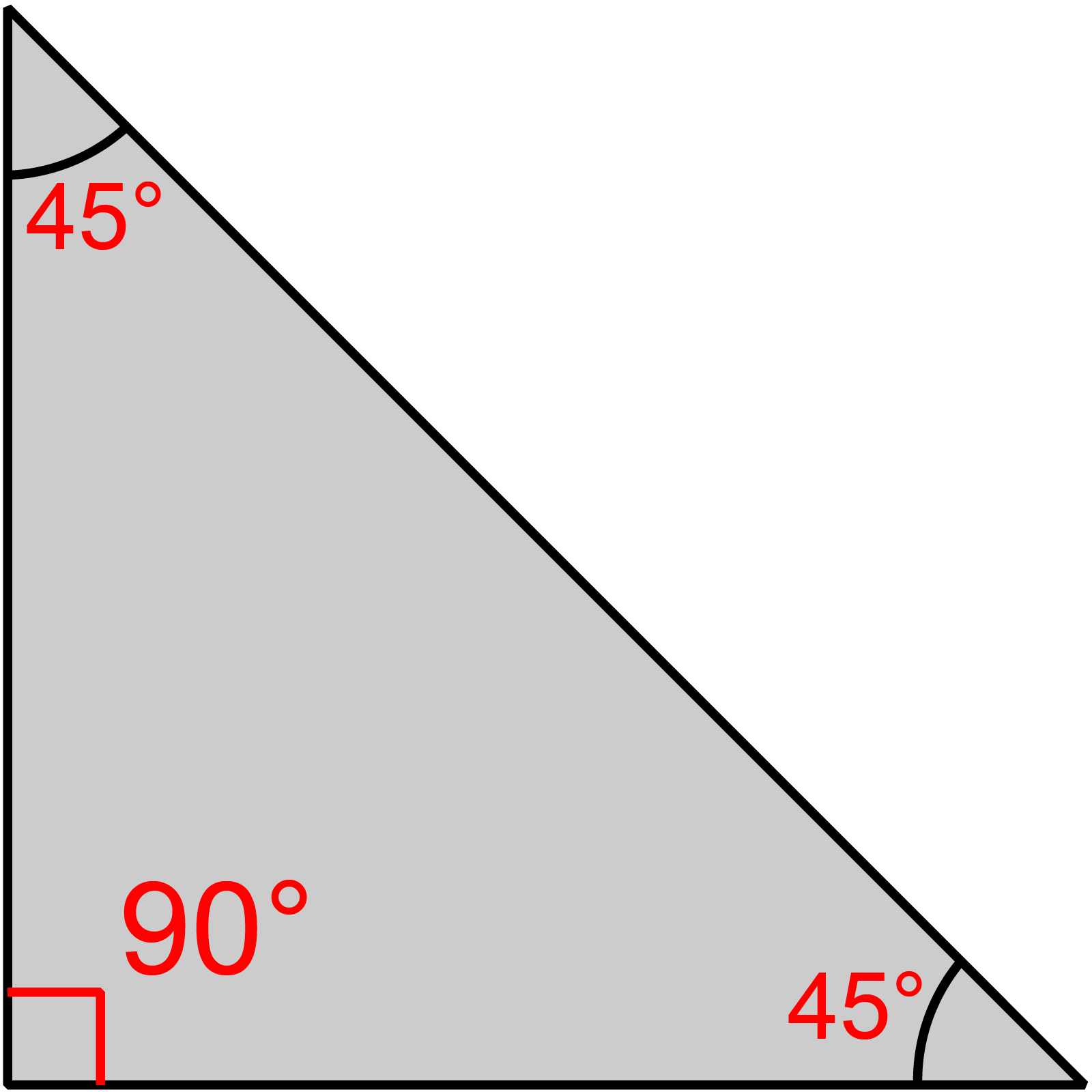
তাই, সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র = (লম্ব + ভূমি + অতিভুজ) একক।
বা, সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র = (লম্ব + লম্ব + অতিভুজ) একক।
বা, সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র = (২ ⨯ লম্ব + অতিভুজ) একক।

অথবা, সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র = (২ ⨯ ভূমি + অতিভুজ) একক।

সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন সমান বাহুদ্বয়ের দৈর্ঘ্য a একক এবং অতিভুজের দৈর্ঘ্য b একক হলে
সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র = (2a + b) একক।