মৌলিক সংখ্যা কাকে বলে
এই টিউটোরিয়ালটি শেষে -
মৌলিক সংখ্যা কাকে বলে - তা বর্ণনা করতে পারা যাবে।
মৌলিক সংখ্যাকে একাধিকভাবে সংজ্ঞায়িত করতে পারা যাবে।
একটি স্বাভাবিক সংখ্যা মৌলিক সংখ্যা কিনা - তা নির্ণয় করতে পারা যাবে।
১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা কতটি বা কয়টি এবং যেকোনো সংখ্যা পর্যন্ত মৌলিক সংখ্যার তালিকা নির্ণয় করতে পারা যাবে।
মৌলিক সংখ্যা কি
যে স্বাভাবিক সংখ্যার কেবল দুইটি পৃথক উৎপাদক ১ এবং ঐ সংখ্যাটি নিজে - তাকে মৌলিক সংখ্যা বলে। যেমনঃ ৫ একটি মৌলিক সংখ্যা। কারণ, স্বাভাবিক সংখ্যা ৫ কে কেবল ৫ = ১×৫ আকারে প্রকাশ করা যায়। তাই ৫ এর কেবল দুইটি পৃথক উৎপাদক হলো ১ এবং ৫। একারণে ৫ একটি মৌলিক সংখ্যা। তদ্রূপ- ২, ৩, ৭, ১১, ১৩ ইত্যাদি এক-একটি মৌলিক সংখ্যা।
যে সংখ্যাকে অন্য কোনো সংখ্যা দ্বারা ভাগ করলে নিঃশেষে বিভাজ্য হয় না তাকে মৌলিক সংখ্যা বলে।

অন্যভাবে বললে, যে সংখ্যাকে অন্য কোনো সংখ্যা দ্বারা ভাগ করলে ভাগশেষ থাকে তাকে মৌলিক সংখ্যা বলে।
যে সংখ্যাকে ১ ও সেই সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না তাকে মৌলিক সংখ্যা বলে।
১ অপেক্ষা বড় যেসব সংখ্যার ১ এবং ঐ সংখ্যা ছাড়া অন্য কোনো গুণনীয়ক বা উৎপাদক নেই তাকে মৌলিক সংখ্যা বলে।
যে সংখ্যাটির গুণনীয়ক বা উৎপাদক কেবল ১ এবং ঐ সংখ্যাটি নিজে তাকে মৌলিক সংখ্যা বলে।
যে সংখ্যা শুধু ১ এবং ঐ সংখ্যা দ্বারা বিভাজ্য, অন্য কোনো সংখ্যা দ্বারা বিভাজ্য নয় তাকে মৌলিক সংখ্যা বলে।
সহজভাবে বলা যায়, যে সংখ্যাকে অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না তাকে মৌলিক সংখ্যা বলে।
যেমনঃ ১৭ একটি মৌলিক সংখ্যা। কারণ, ১৭ সংখ্যাটি অন্য কোনো সংখ্যা দ্বারা নিঃশেষে বিভাজ্য নয়; ১৭ সংখ্যাটিকে অন্য কোনো সংখ্যা দ্বারা ভাগ করলে ভাগশেষ থাকে; অর্থাৎ, ১৭ সংখ্যাটিকে অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না।
১ অপেক্ষা বড় যে স্বাভাবিক সংখ্যাকে তার চেয়ে ছোট দুইটি স্বাভাবিক সংখ্যার গুণফলরূপে প্রকাশ করা যায় না তাকে মৌলিক সংখ্যা বলে। স্বাভাবিক সংখ্যা বলতে ১, ২, ৩, .......,১০০, ১০১, ১০২, ....... ইত্যাদি সকল ধনাত্মক পূর্ণ সংখ্যাকে বুঝায়। যেমনঃ ১৯ হলো ১ এর চেয়ে বড় একটি স্বাভাবিক সংখ্যা। কিন্তু ১৯ কে ১৯ এর চেয়ে ছোট দুইটি স্বাভাবিক সংখ্যার গুণফল আকারে প্রকাশ করা যায় না। তাই ১৯ একটি মৌলিক সংখ্যা। আবার ১৯ কে ১৯ = ১ ⨯ ১৯ আকারে লিখা যায় অর্থাৎ, ১ ও ১৯ এর গুণফলরপে প্রকাশ যায় বটে; কিন্তু একটি সংখ্যা ১, ১৯ অপেক্ষা ছোট হলেও অপর একটি সংখ্যা ১৯, যা ১৯ অপেক্ষা ছোট নয়। তাই সংজ্ঞা অনুসারে, ১৯ একটি মৌলিক সংখ্যা।
আবার, ২১ = ৩ ⨯ ৭ অর্থাৎ, ২১ কে দুইটি স্বাভাবিক সংখ্যার গুণফলরপে প্রকাশ করা যায়। তাই ২১ কোনো মৌলিক সংখ্যা নয়। তাহলে ২১ একটি যৌগিক সংখ্যা।
তাই বলা যায়, ১ অপেক্ষা বড় যেসকল পূর্ণসংখ্যা মৌলিক সংখ্যা নয় তাদেরকে যৌগিক সংখ্যা বলে।
সংখ্যা জগতে ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯ যে দশটি অংক রয়েছে, তার মধ্যে ২, ৩, ৫ এবং ৭ অংকগুলোর প্রত্যেকেই এক-একটি মৌলিক সংখ্যা।
ইরাটোস্থিনিস ছাঁকনির সাহায্যে মৌলিক সংখ্যা নির্ণয়
ইরাটোস্থিনিস ছাঁকনির সাহায্যে খুব সহজেই মৌলিক সংখ্যা নির্ণয় করা যায়। এই ছাঁকনি ব্যবহার করে একটি নির্দিষ্ট সংখ্যা থেকে অন্য আরেকটি নির্দিষ্ট সংখ্যা পর্যন্ত মৌলিক সংখ্যা নির্ণয় করা যায়। এখানে ১ থেকে শুরু করে ১০০ পর্যন্ত সংখ্যা লিখে মৌলিক সংখ্যা নির্ণয় করা হয়েছে। নিচে ইরাটোস্থিনিস ছাঁকনির সাহায্যে মৌলিক সংখ্যা নির্ণয় পদ্ধতি বর্ণনা করা হলো।
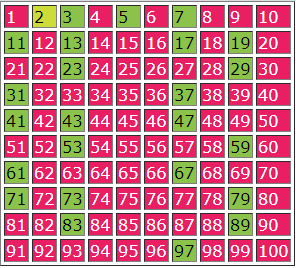
প্রথম ধাপঃ ১ থেকে শুরু করে ১০০ পর্যন্ত সংখ্যাগুলো একটি ছকে লিখি।
দ্বিতীয় ধাপঃ ১ কেটে দিই এবং সবচেয়ে ছোট মৌলিক সংখ্যা ২ এর গুণিতকসমূহ কেটে দিই, যা লাল কালি দ্বারা বুঝানো হয়েছে।
তৃতীয় ধাপঃ তারপর ধারাবাহিকভাবে ছোট মৌলিক সংখ্যা ৩, ৫, ৭, ১১ ইত্যাদি মৌলিক সংখ্যাগুলোর গুণিতকসমূহ কেটে দিই, যা লাল কালি দ্বারা চিহ্নিত করা হয়েছে।
চতুর্থ ধাপঃ তারপর তালিকার অবশিষ্ট সংখ্যাসমূহ চিহ্নিত করি এবং এগুলো সবই মৌলিক সংখ্যা, যা হালকা সবুজ কালি দ্বারা চিহ্নিত করা হয়েছে। উল্লেখ্য, এখানে ২ মৌলিক সংখ্যা হলেও ২ কে হালকা হলুদ কালি দ্বারা চিহ্নিত করা হয়েছে কারণ, সংখ্যাজগতে ২ হলো একমাত্র জোড় মৌলিক সংখ্যা। একথাটি বুঝানোর জন্যই ২ কে ভিন্নভাবে চিহ্নিত করা হয়েছে।
এভাবে, ১ থেকে শুরু করে ১০০ পর্যন্ত প্রাপ্ত মৌলিক সংখ্যাগুলো হলোঃ ২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১, ৩৭, ৪১, ৪৩, ৪৭, ৫৩, ৫৯, ৬১, ৬৭, ৭১, ৭৩, ৭৯, ৮৩, ৮৯ ও ৯৭। সুতরাং ১ থেকে শুরু করে ১০০ পর্যন্ত মৌলিক সংখ্যা মোট ২৫টি।
আবার, ১ থেকে শুরু করে ২১০ পর্যন্ত সংখ্যাগুলোর মধ্যে মৌলিক সংখ্যা নির্ণয় করে দেখানো হলো।
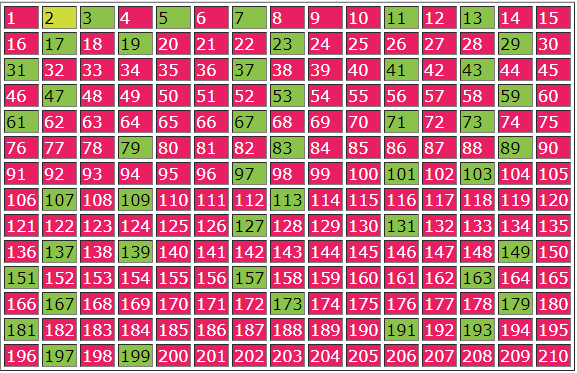
প্রথম ধাপঃ ১ থেকে শুরু করে ২১০ পর্যন্ত সংখ্যাগুলো একটি তালিকায় লিখি।
দ্বিতীয় ধাপঃ ১ কেটে দিই এবং সবচেয়ে ক্ষুদ্রতম মৌলিক সংখ্যা ২ এর গুণিতকগুলো কেটে দিই, যা লাল কালি দ্বারা বুঝানো হয়েছে।
তৃতীয় ধাপঃ তারপর ক্রমান্বয়ে ক্ষুদ্রতর মৌলিক সংখ্যা ৩, ৫, ৭, ১১, ১৩, ১৭ ইত্যাদি মৌলিক সংখ্যাগুলোর গুণিতকসমূহ কেটে দিই, যা লাল কালি দ্বারা চিহ্নিত করা হয়েছে।
চতুর্থ ধাপঃ তারপর তালিকার অবশিষ্ট সংখ্যাগুলো চিহ্নিত করি এবং এগুলো সবই মৌলিক সংখ্যা, যা হালকা সবুজ কালি দ্বারা চিহ্নিত করা হয়েছে। এখানে উল্লেখ করা যেতে পারে, ২ মৌলিক সংখ্যা হলেও ২ কে হালকা হলুদ কালি দ্বারা চিহ্নিত করা হয়েছে কারণ, সংখ্যাজগতে ২ হলো একমাত্র জোড় মৌলিক সংখ্যা। একথাটি বুঝানোর জন্যই ২ কে ভিন্নভাবে চিহ্নিত করা হয়েছে।
এভাবে, ১ থেকে ২১০ পর্যন্ত প্রাপ্ত মৌলিক সংখ্যাগুলো হলোঃ ২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১, ৩৭, ৪১, ৪৩, ৪৭, ৫৩, ৫৯, ৬১, ৬৭, ৭১, ৭৩, ৭৯, ৮৩, ৮৯ , ৯৭, ১০১, ১০৩, ১০৭, ১০৯, ১১৩, ১২৭, ১৩১, ১৩৭, ১৩৯, ১৪৯, ১৫১, ১৫৭, ১৬৩, ১৬৭, ১৭৩, ১৭৯, ১৮১, ১৯১, ১৯৩, ১৯৭ ও ১৯৯। সুতরাং ১ থেকে শুরু করে ২১০ পর্যন্ত মোট ৪৬টি মৌলিক সংখ্যা আছে।
ইরাটোস্থিনিস ছাঁকনির সাহায্যে একটি নির্দিষ্ট সংখ্যা থেকে অন্য একটি নির্দিষ্ট সংখ্যা পর্যন্ত মৌলিক সংখ্যা নির্ণয়ের এ্যাপ
উপরে সংখ্যা লিখে "ইরাটোস্থিনিস ছাঁকনি তৈরি" বাটনে ক্লিক করলে ইরাটোস্থিনিস ছাঁকনি ও মৌলিক সংখ্যাগুলো পাওয়া যায়।
সর্ববৃহৎ মৌলিক সংখ্যা আবিষ্কারের ইতিহাস
গণিতবিদগণ প্রতিনিয়ত নতুন নতুন মৌলিক সংখ্যা আবিষ্কারের জন্য অবিরত কাজ করে যাচ্ছেন। ২০০৯ খি. পর্যন্ত সর্ববৃহৎ যে মৌলিক সংখ্যাটি আবিষ্কৃত হয়েছিল তা ২৪,৩১,১২,৬০৯ - ১। এপ্রিল ২০২১ খ্রি. পর্যন্ত যতগুলো মৌলিক সংখ্যা আবিস্কৃত হয়েছে, তার মধ্যে সবচেয়ে বড় যে মৌলিক সংখ্যা পাওয়া গেছে তা হলো ২৮,২৫,৮৯,৯৩৩ - ১ যার অংক সংখ্যা ২,৪৮,৬২,০৪৮২ টি। তারপরও গণিতবিদগণ এর চেয়ে বড় বড় মৌলিক সংখ্যা আবিষ্কারের জন্য প্রচেষ্টা চালিয়ে যাচ্ছেন। নিচে সর্বশেষ বিগত কয়েক বছরের মৌলিক সংখ্যা আবিষ্কারের ইতিহাস তুলে ধরা হলোঃ
| মৌলিক সংখ্যার ধরণ | মৌলিক সংখ্যা | মৌলিক সংখ্যাটির অংক সংখ্যা | আবিষ্কারের তারিখ |
|---|---|---|---|
| Primorial prime | ১০,৯৮,১৩৩# - ১ | ৪,৭৬,৩১১ টি | মার্চ ২০১২ |
| Factorial prime | ২,০৮,০০৩! - ১ | ১০,১৫,৮৪৩ টি | জুলাই ২০১৬ |
| Twin primes | ২৯৯৬৮৬,৩০,৩৪,৮৯৫ × ২১২,৯০,০০০±১ | ৩,৮৮,৩৪২ টি | সেপ্টেম্বর ২০১৬ |
| Proth prime | ১০,২২৩ × ২৩,১১,৭২,১৬৫ + ১ | ৯৩,৮৩,৭৬১ টি | ৩১ অক্টোবর ২০১৬ |
| Mersenne prime | ২৭,৭২,৩২,৯১৭ - ১ | ২,৩২,৪৯,৪২৫ টি | ২৬ ডিসেম্বর ২০১৭ |
| Mersenne prime | ২৮,২৫,৮৯,৯৩৩ - ১ | ২,৪৮,৬২,০৪৮২ টি | ৭ ডিসেম্বর ২০১৮ |
মৌলিক সংখ্যার ধর্ম
মৌলিক সংখ্যার অনেক ধর্ম রয়েছে এবং এর উপর ভিত্তি করে অনেক উপপাদ্য তৈরি হয়েছে। মৌলিক সংখ্যার এসব ধর্মগুলোর মধ্যে দুই-একটি চমৎকার ধর্ম হলোঃ
- যেকোনো জোড় সংখ্যাকে দুইটি মৌলিক সংখ্যার যোগফল আকারে প্রকাশ করা যায়। যেমনঃ একটি জোড় সংখ্যা ৮ = ৩ + ৫, যা দুইটি মৌলিক সংখ্যার সমষ্টি। আবার আরেকটি জোড় সংখ্যা ৫০ = ৭ + ৪৩, যা দুইটি মৌলিক সংখ্যার যোগফল। এরূপ যেকোনো জোড় সংখ্যাকে দুইটি মৌলিক সংখ্যার যোগফল আকারে লিখা যায়।
- ৩ অপেক্ষা বড় যেকোনো মৌলিক সংখ্যার বর্গকে ১২ দ্বারা ভাগ করলে ১ অবশিষ্ট থাকে। যেমন, ৩ অপেক্ষা বড় মৌলিক সংখ্যা হলো ৫ যার বর্গ ২৫, যাকে ১২ দ্বারা ভাগ করলে ১ অবশিষ্ট থাকে। আবার, অপর একটি মৌলিক সংখ্যা ১১ যার বর্গ ১২১, যাকে ১২ দ্বারা ভাগ করলে ১ অবশিষ্ট থাকে। এরকম ১৩, ১৭, ১৯, ২৩ ইত্যাদি প্রত্যেকটি মৌলিক সংখ্যার বর্গকে ১২ দ্বারা ভাগ করলে ১ অবশিষ্ট থাকে।
১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা
১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা নির্ণয়ের আগে একে ক্ষুদ্র ক্ষুদ্র কয়েকটি অংশে বিভক্ত করি।
- ১ থেকে ১০ পর্যন্ত মৌলিক সংখ্যা সমূহ ২, ৩, ৫, ৭। সুতরাং, ১ থেকে ১০ পর্যন্ত মৌলিক সংখ্যা ৪টি।
- ১১ থেকে ২০ পর্যন্ত মৌলিক সংখ্যা সমূহ ১১, ১৩, ১৭, ১৯। সুতরাং, ১১ থেকে ২০ পর্যন্ত মৌলিক সংখ্যা ৪টি।
- ২১ থেকে ৩০ পর্যন্ত মৌলিক সংখ্যা সমূহ ২৩, ২৯। সুতরাং, ২১ থেকে ৩০ পর্যন্ত মৌলিক সংখ্যা ২টি।
- ৩১ থেকে ৪০ পর্যন্ত মৌলিক সংখ্যা সমূহ ৩১, ৩৭। সুতরাং, ৩১ থেকে ৪০ পর্যন্ত মৌলিক সংখ্যা ২টি।
- ৪১ থেকে ৫০ পর্যন্ত মৌলিক সংখ্যা সমূহ ৪১, ৪৩, ৪৭। সুতরাং, ৪১ থেকে ৫০ পর্যন্ত মৌলিক সংখ্যা ৩টি।
- ৫১ থেকে ৬০ পর্যন্ত মৌলিক সংখ্যা সমূহ ৫৩, ৫৯। সুতরাং, ৫১ থেকে ৬০ পর্যন্ত মৌলিক সংখ্যা ২টি।
- ৬১ থেকে ৭০ পর্যন্ত মৌলিক সংখ্যা সমূহ ৬১, ৬৭। সুতরাং, ৬১ থেকে ৭০ পর্যন্ত মৌলিক সংখ্যা ২টি।
- ৭১ থেকে ৮০ পর্যন্ত মৌলিক সংখ্যা সমূহ ৭১, ৭৩, ৭৯। সুতরাং, ৭১ থেকে ৮০ পর্যন্ত মৌলিক সংখ্যা ৩টি।
- ৮১ থেকে ৯০ পর্যন্ত মৌলিক সংখ্যা সমূহ ৮৩, ৮৯। সুতরাং, ৮১ থেকে ৯০ পর্যন্ত মৌলিক সংখ্যা ২টি।
- ৯১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা সমূহ ৯৭। সুতরাং, ৯১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা ১টি।
১ থেকে ১০০ পর্যন্ত সংখ্যাগুলো বিশ্লেষণ করলে মোট ২৫টি মৌলিক সংখ্যা পাওয়া যায়। ১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা সমূহ নিম্নরূপঃ
২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১, ৩৭, ৪১, ৪৩, ৪৭, ৫৩, ৫৯, ৬১, ৬৭, ৭১, ৭৩, ৭৯, ৮৩, ৮৯ ও ৯৭।
এ্যাপের সাহায্যে মৌলিক সংখ্যা নির্ণয়
যেকোনো একটি ছোট সংখ্যা মৌলিক কিনা তা খুব সহজে নির্ণয় করা সম্ভব হলেও বড় একটি সংখ্যা মৌলিক কিনা তা নির্ণয় করা সত্যিই একটি দুরহ বিষয়। এ্যাপটির সাহায্যে যেকোনো একটি সংখ্যা মৌলিক কিনা তা নির্ণয় করা যায়। এই এ্যাপটির “সংখ্যা লিখি” স্থলে যেকোনো সংখ্যা লিখে “মৌলিক নির্ণয়” বাটনে ক্লিক করলে তা নির্ণয় হয়ে যায়।
মৌলিক সংখ্যা নির্ণয়ের এ্যাপ
379387 মৌলিক সংখ্যা
উপরে যেকোনো একটি সংখ্যা লিখে “মৌলিক নির্ণয়” বাটনে ক্লিক করলে ফলাফল পাওয়া যায়।
মৌলিক সংখ্যা তালিকা নির্ণয়
অন্যভাবে বললে, যেসব স্বাভাবিক সংখ্যা ১ এবং ঐ সংখ্যা ব্যতীত অন্য কোনো স্বাভাবিক সংখ্যা দ্বারা নিঃশেষে বিভাজ্য নয়, তাদেরকে মৌলিক সংখ্যা বলে। অন্যথায়, সংখ্যাগুলো যৌগিক সংখ্যা। নিঃশেষে বিভাজ্য বলতে বুঝায়, কোনো একটি স্বাভাবিক সংখ্যাকে অন্য কোনো স্বাভাবিক সংখ্যা দ্বারা ভাগ করলে যদি কোনো ভাগশেষ বা অবশিষ্ট না থাকে। উদাহরণস্বরূপ, ২৩ একটি স্বাভাবিক সংখ্যা। এই সংখ্যাটি ১ এবং ২৩ ব্যতীত অন্য কোনো স্বাভাবিক সংখ্যা দ্বারা ভাগ করলে নিঃশেষে বিভাজ্য হয় না অর্থাৎ, অন্য কোনো সংখ্যা দ্বারা ভাগ করলে দেখা যায় কিছু অবশিষ্ট থাকে। অতএব, ২৩ একটি মৌলিক সংখ্যা।
আবার ২২ একটি স্বাভাবিক সংখ্যা। এই সংখ্যাটি ১ এবং ২২ ব্যতীত আরও দুইটি সংখ্যা ২ ও ১১ দ্বারা নিঃশেষে বিভাজ্য। সুতরাং, ২২ সংখ্যাটি কোনো মৌলিক সংখ্যা নয়। এটি একটি যৌগিক সংখ্যা।
১ থেকে নির্দিষ্ট সংখ্যা পর্যন্ত মৌলিক সংখ্যা নির্ণয়ের এ্যাপ
উপরে সংখ্যা লিখে "Get Prime" বাটনে ক্লিক করলে ১ থেকে ঐ সংখ্যা পর্যন্ত মৌলিক সংখ্যা পাওয়া যায়।
সকল মৌলিক সংখ্যা ১ অপেক্ষা বড়। আর ২ হলো একমাত্র জোড় মৌলিক সংখ্যা। ২ ব্যতীত আর কোনো জোড় সংখ্যা মৌলিক হতে পারে না; কারণ ঐ সব জোড় সংখ্যাকে ২ দ্বারা ভাগ করলে নিঃশেষে বিভাজ্য হয়। আবার, সব যৌগিক সংখ্যাও ১ অপেক্ষা বড়। কারণ ১ অপেক্ষা বড় যেসব স্বাভাবিক সংখ্যা মৌলিক নয়; তাই যৌগিক সংখ্যা। কাজেই দেখা যাচ্ছে যে, কোনো একটি সংখ্যা মৌলিক সংখ্যা হোক বা যৌগিক সংখ্যা হোক, তা অবশ্যই ১ অপেক্ষা বড়।