ঘনবস্তু কাকে বলে

ঘনবস্তু কি

যে ত্রি-মাত্রিক জ্যামিতিক আকার দৈর্ঘ্য, প্রস্থ ও উচ্চতা বরাবর তিনটি মাত্রায় স্থান দখল করে তাকে ঘনবস্তু বলে। অতএব, ঘনবস্তু হলো ত্রি-মাত্রিক জ্যামিতিক আকার যা তিনটি মাত্রায় স্থান ধারণ করে। এর মাত্রা তিনটি হলো দৈর্ঘ্য, প্রস্থ এবং উচ্চতা।

সহজ কথায়, ত্রিমাত্রিক বস্তুই ঘনবস্তু। আর ত্রিমাত্রিক বস্তু হলো ত্রিমাত্রিক জগতের বস্তু। ত্রিমাত্রিক জগতের বস্তু বলতে বুঝায়, যে বস্তুর অবস্থান নির্ণয় করার জন্য তিনটি মাত্রা অর্থাৎ দৈর্ঘ্য, প্রস্থ ও উচ্চতার প্রয়োজন হয়।

তাই বলা হয়, দৈর্ঘ্য, প্রস্থ ও উচ্চতার সাহায্যে যে বস্তুর অবস্থান নির্ণয় করা হয়, তাকে ঘনবস্তু বলে।

অন্যভাবে বলা যায়, ত্রিমাত্রিক জগতে যে বস্তু স্থান দখল করে তাকে ঘনবস্তু বলে।

জ্যামিতির ভাষায়, ঘনবস্তু হলো এমন একটি আবদ্ধ ত্রিমাত্রিক স্থান যা কিছু নির্দিষ্ট তল (surface) দ্বারা সীমাবদ্ধ থাকে। এই তলগুলো সমতল (plane) অথবা বক্রতল (curved surface) হতে পারে।

সব ঘনবস্তুই ঘন জ্যামিতির অন্তর্ভূক্ত।

ঘন জ্যামিতি মূলতঃ ঘনবস্তুর আয়তন পরিমাপের জন্য ব্যবহৃত হয়।

ঘনবস্তু কয় প্রকার ও কি কি

ঘনবস্তুকে তাদের আকৃতি এবং গঠন অনুযায়ী বিভিন্ন ভাগে ভাগ করা যায়। এদের মধ্যে কিছু উল্লেখযোগ্য প্রকারভেদ হলো:

• নিয়মিত ঘনবস্তু (Regular Solid)
• অনিয়মিত ঘনবস্তু (Irregular Solid)
• বহুভুজাকার ঘনবস্তু (Polyhedron)
• বৃত্তাকার ঘনবস্তু (Rounded Solid)

নিচে সকল প্রকার ঘনবস্তুর সংক্ষিপ্ত বর্ণনা করা হলো।

• নিয়মিত ঘনবস্তু: যে ঘনবস্তুর সব পৃষ্ঠ এবং কোণ সমান তাকে নিয়মিত ঘনবস্তু বলে। যেমন ঘনক।
• অনিয়মিত ঘনবস্তু: যে ঘনবস্তুর পৃষ্ঠসমূহ বা কোণ সমান নয় তাকে অনিয়মিত ঘনবস্তু বলে। যেমন পিরামিড।
• বহুভুজাকার ঘনবস্তু: যে সকল ঘনবস্তু শুধুমাত্র সমতল বহুভুজ দ্বারা সীমাবদ্ধ থাকে, তাদেরকে বহুভুজাকার ঘনবস্তু বলে। এর কিছু উদাহরণ হলো:
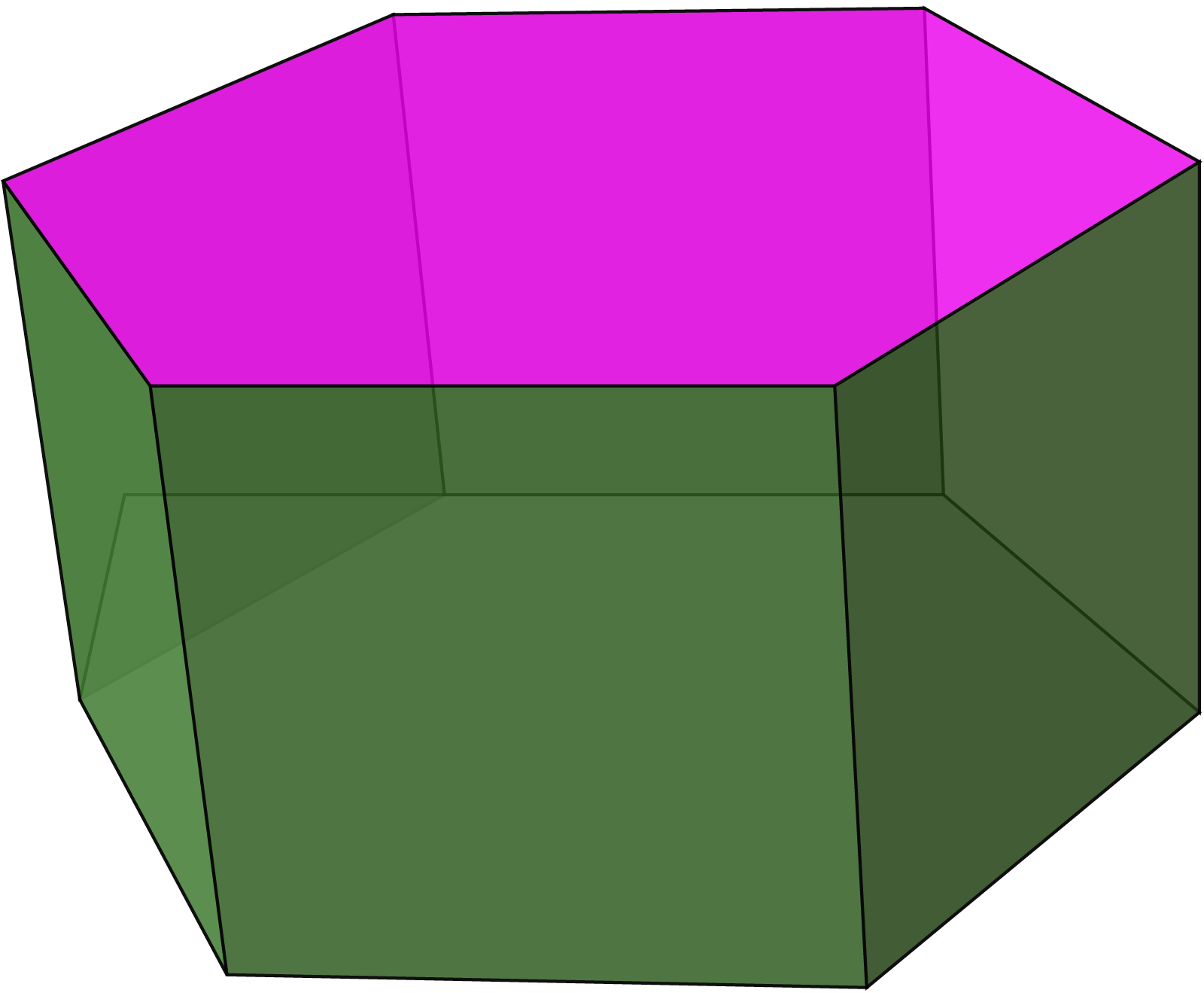
  • প্রিজম (Prism): এর দুটি সমান্তরাল এবং সর্বসম বহুভুজাকার ভূমি এবং আয়তাকার পার্শ্বতল থাকে।
  • পিরামিড (Pyramid): এর একটি বহুভুজাকার ভূমি এবং ত্রিভুজাকার পার্শ্বতল একটি সাধারণ শীর্ষবিন্দুতে মিলিত হয়।
  • ঘনক (Cube): ছয়টি বর্গাকার তল দ্বারা সীমাবদ্ধ।
  • আয়তাকার ঘনবস্তু (Cuboid): ছয়টি আয়তাকার তল দ্বারা সীমাবদ্ধ।
  • চতুস্তলক (Tetrahedron): চারটি ত্রিভুজাকার তল দ্বারা সীমাবদ্ধ।
• বৃত্তাকার ঘনবস্তু: যে সকল ঘনবস্তুর এক বা একাধিক তল বক্রাকার হয়, তাদেরকে বৃত্তাকার ঘনবস্তু বলে। এর কিছু উদাহরণ হলো:
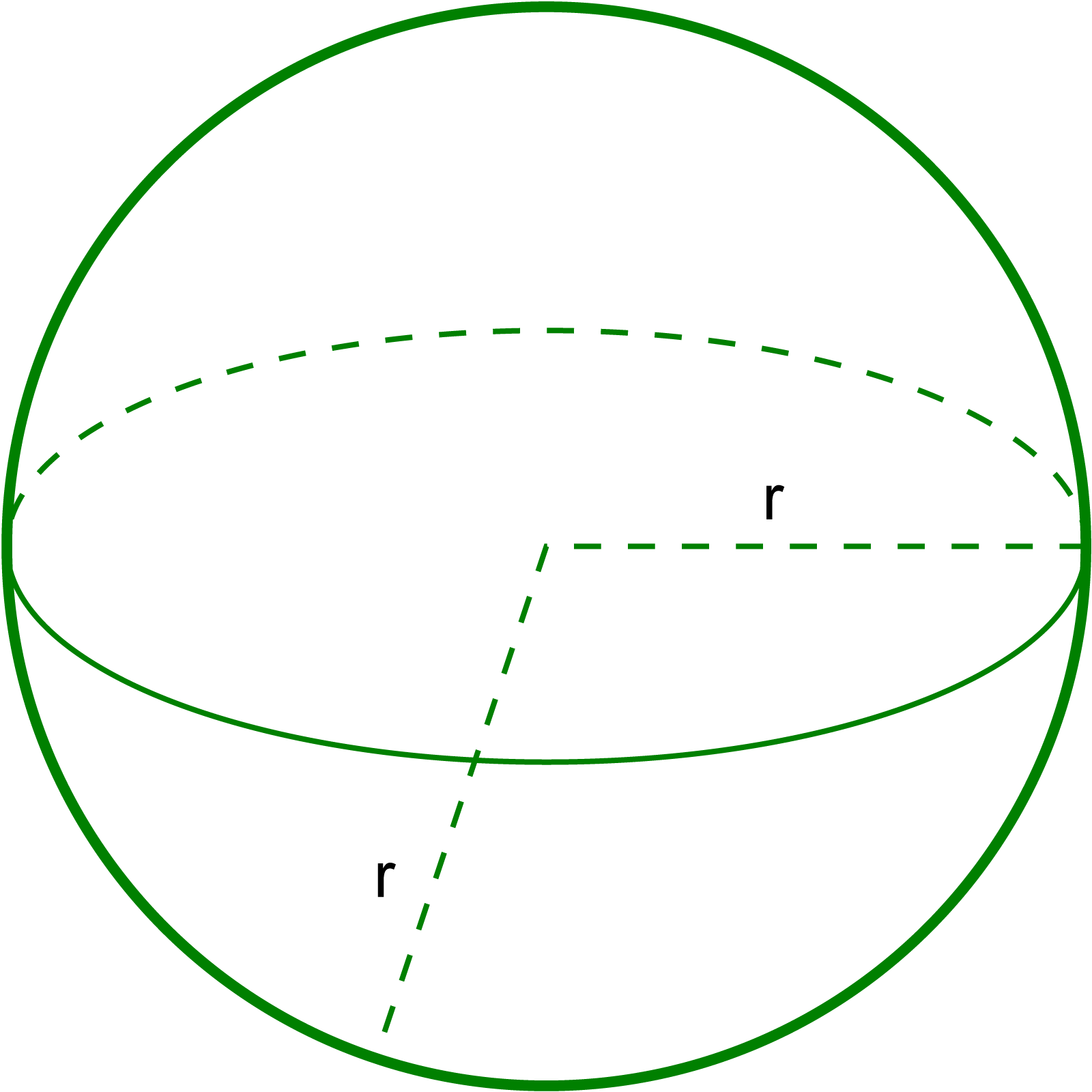
  • গোলক (Sphere): একটি নির্দিষ্ট কেন্দ্র থেকে সমদূরবর্তী সকল বিন্দুর সমন্বয়ে গঠিত। এর কোন ধার বা শীর্ষবিন্দু নেই।
  • সিলিন্ডার বা বেলন (Cylinder): দুটি সমান্তরাল এবং সর্বসম বৃত্তাকার ভূমি এবং একটি বক্রতল দ্বারা গঠিত।
  • কোণক বা শঙ্কু (Cone): একটি বৃত্তাকার ভূমি এবং একটি বক্রতল যা একটি নির্দিষ্ট শীর্ষবিন্দুতে মিলিত হয়।

সুষম ঘনবস্তু কাকে বলে

যে ঘনবস্তুর ধারগুলো পরস্পর সমান তাকে সুষম ঘনবস্তু বলে। অন্যভাবে বললে, যে ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা পরস্পর সমান তাকে সুষম ঘনবস্তু বলে। যেমন: ঘনক।

অসম ঘনবস্তু কাকে বলে

যে ঘনবস্তুর ধারগুলো পরস্পর অসমান তাকে অসম ঘনবস্তু বলে। আবার, অসম ঘনবস্তুকে আরেকভাবে সংজ্ঞায়িত করা যায় তা হলো- যে ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা পরস্পর সমান নয় তাকে অসম ঘনবস্তু বলে। যেমন: আয়তাকার ঘনবস্তু।

ঘনবস্তুর মাত্রা কয়টি ও কি কি

এখন আমরা ঘনবস্তুর মাত্রা কয়টি ও কি কি তা জানার চেষ্টা করি। যেকোনো ঘনবস্তুর অবস্থান পরিমাপ করার জন্য দৈর্ঘ্য, প্রস্থ ও উচ্চতা- এই তিনটি মাত্রার প্রয়োজন হয়। একারণে ঘনবস্তুর মাত্রা তিনটি। আর একারণেই ঘনবস্তু ত্রিমাত্রিক জ্যামিতির অন্তর্ভূক্ত।

ঘনবস্তুর তল কয়টি

যেকোনো ঘনবস্তুর তল কয়টি তা এক কথায় বলা যায় না। এক-একটি ঘনবস্তুর তল সংখ্যা এক-এক রকম। কয়েকটি ঘনবস্তুর তল সংখ্যা নিচে উল্লেখ করা হলো।

• আয়তাকার ঘনবস্তু: ৬টি আয়তাকার তল বা সমতল।
• ঘনক: ৬টি বর্গাকার তল।
• কোণক: ১টি বৃত্তাকার ভূমি তল ও ১টি পার্শ্ব বক্রতল।
• সিলিন্ডার: ২টি বৃত্তাকার ভূমি তল ও ১টি পার্শ্ব বক্রতল।
• প্রিজম: ২টি বহুভুজাকার সর্বসম ভূমি তল ও বহুভুজের বাহুর সংখ্যার সমান সামান্তরিক আকার পার্শ্ব তল।
• গোলক: ১টি গোলাকৃতি বক্রতল।
• পিরামিড: ১টি বহুভুজাকার ভূমি তল ও বহুভুজের বাহুর সংখ্যার সমান ত্রিভুজাকার পার্শ্ব তল।

ঘনবস্তুর উপাদান

যেকোনো ঘনবস্তু বিশ্লেষণ করলে নিম্নের তিনটি উপাদান পাওয়া যায়।

1. পৃষ্ঠতল (Surface): ঘনবস্তুর বাইরের দিক যেটি তাকে সীমানা দেয়।
2. ক্ষেত্রফল (Area): ঘনবস্তুর বাহ্যিক পৃষ্ঠের পরিমাণ।
3. আয়তন (Volume): ঘনবস্তুর ভেতরের স্থান বা স্পেস, যা তার পরিমাপকে নির্দেশ করে।

ঘনবস্তুর গঠন পদ্ধতি

প্রথম চিত্রে, একটি স্থির বিন্দু দেখা যাচ্ছে।

দ্বিতীয় চিত্রে, অসংখ্য বিন্দু সোজা বরাবর পরস্পর যুক্ত হয়ে রেখা তৈরি করে।

তৃতীয় চিত্রে, একটির পর আরেকটি রেখা পরস্পর স্থাপিত হয়ে তল উৎপন্ন হচ্ছে।

পরিশেষে, তৃতীয় চিত্র থেকে তল তৈরি হয়ে, এরূপ ছয়টি তল মিলে একটি ঘনবস্তু তথা আয়তাকার ঘনবস্তু তৈরি করছে।

ঘনবস্তুর বৈশিষ্ট্য

ঘনবস্তু বিশ্লেষণ করলে এর কতকগুলো বৈশিষ্ট্য পরিলক্ষিত হয়। ঘনবস্তুর কয়েকটি বৈশিষ্ট্য নিচে উল্লেখ করা হলো।

• তিনটি মাত্রা: ঘনবস্তুর অপরিহার্য বৈশিষ্ট্য হলো এর তিনটি মাত্রা - দৈর্ঘ্য, প্রস্থ এবং উচ্চতা। এই তিনটি মাত্রার উপস্থিতির কারণেই এটি ত্রিমাত্রিক স্থানে একটি আয়তন (volume) ধারণ করে।
• আয়তন: ঘনবস্তুর একটি নির্দিষ্ট আয়তন থাকে। এই আয়তন দ্বারা বোঝা যায় যে বস্তুটি ত্রিমাত্রিক স্থানে কতটা জায়গা জুড়ে রয়েছে।
• তল (Surface): ঘনবস্তু এক বা একাধিক তল দ্বারা গঠিত। এই তলগুলো ঘনবস্তুর সীমানা নির্ধারণ করে।
• ধার (Edge): দুটি তল যেখানে মিলিত হয়, তাকে ধার বলে। ঘনবস্তুতে একাধিক ধার থাকতে পারে।
• শীর্ষবিন্দু (Vertex): তিন বা ততোধিক ধার যেখানে মিলিত হয়, তাকে শীর্ষবিন্দু বলে। ঘনবস্তুতে এক বা একাধিক শীর্ষবিন্দু থাকতে পারে।

ঘনবস্তুর গুরুত্ব

জ্যামিতির একটি অপরিহার্য অংশ হলো ঘনবস্তু। ত্রিমাত্রিক জগৎ এবং এর বিভিন্ন বৈশিষ্ট্য বোঝার জন্য ঘনবস্তুর ধারণা অত্যন্ত গুরুত্বপূর্ণ। ঘনবস্তুর ধারণা দৈনন্দিন জীবনের বিভিন্ন ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে। এর গুরুত্বের কিছু দিক নিচে উল্লেখ করা হলো:

• অভ্যন্তরীণ স্থান নির্ধারণে: ঘনবস্তুর আয়তন এবং পরিমাপ থেকে আমরা একটি রুম বা ঘরের পরিমাণ নির্ধারণ করতে পারি।
• বিজ্ঞানের ক্ষেত্র: ঘনবস্তুর জ্ঞান বিজ্ঞানে অনেক কাজে লাগে, যেমন রাসায়নিক পদার্থের আয়তন নির্ধারণ বা রকেটের ডিজাইন।
• ইঞ্জিনিয়ারিং ও আর্কিটেকচার: ইঞ্জিনিয়ারিং এবং আর্কিটেকচারে ঘনবস্তুর ডিজাইন এবং পরিমাপের মাধ্যমে স্থাপত্য নির্মাণ করা হয়।
• আয়তন নির্ণয়: ঘনবস্তুর ধারণা আয়তন নির্ণয়ের ভিত্তি স্থাপন করে। বিভিন্ন প্রকার ঘনবস্তুর আয়তন নির্ণয়ের সূত্র জ্যামিতিতে গুরুত্বপূর্ণ।
• পৃষ্ঠতলের ক্ষেত্রফল নির্ণয়: ঘনবস্তুর তলগুলোর ক্ষেত্রফল নির্ণয়ের ধারণা বাস্তব জীবনে বিভিন্ন পরিমাপের জন্য প্রয়োজনীয়।
• বাস্তব জগতের মডেলিং: আমাদের চারপাশের অনেক বস্তুকেই ঘনবস্তুর মাধ্যমে মডেল করা যায়। প্রকৌশল, স্থাপত্য এবং পদার্থবিজ্ঞানে এর ব্যাপক ব্যবহার রয়েছে।
• স্থানিক ধারণা (Spatial Reasoning): ঘনবস্তু নিয়ে পড়াশোনা ত্রিমাত্রিক স্থানে বস্তুর অবস্থান এবং পারস্পরিক সম্পর্ক বোঝার ক্ষমতা বৃদ্ধি করে।

চিত্রসহ বিভিন্ন প্রকার ঘনবস্তুর তালিকা

আয়তাকার ঘনবস্তু

ঘনক

সিলিন্ডার

কোণক

গোলক

প্রিজম

পিরামিড

উপসংহার

ঘনবস্তু কেবল জ্যামিতির একটি তাত্ত্বিক ধারণাই নয়, এটি আমাদের দৈনন্দিন জীবনের অবিচ্ছেদ্য অংশ। এর সংজ্ঞা, বৈশিষ্ট্য এবং প্রকারভেদ সম্পর্কে স্পষ্ট ধারণা থাকলে গণিত এবং বাস্তব জগৎকে ভালোভাবে বুঝতে সাহায্য করে। আশা করি, এই আর্টিকেলের মাধ্যমে ঘনবস্তু সম্পর্কে আপনাদের একটি সুস্পষ্ট ধারণা তৈরি হয়েছে।