ঘনক ও ঘনকের আয়তন
এই টিউটোরিয়ালটি শেষে -
ঘনক কি তা বলতে পারা যাবে।
ঘনকের ক্ষেত্রফল এর সূত্র উদ্ভাবন করতে পারা যাবে।
ঘনকের আয়তন ব্যাখ্যা করতে পারা যাবে।
ঘনকের কর্ণের দৈর্ঘ্য নির্ণয় করতে পারা যাবে।
ঘনক
পরস্পর লম্ব ছয়টি বর্গাকার সর্বসম তল দ্বারা যে বহুতলক গঠিত তাকে ঘনক বলে।
ঘনক হলো আয়তাকার ঘনবস্তুর বিশেষ রূপ।
একটি ঘনকের চিত্র এর পৃষ্ঠতল, ধার ও শীর্ষসমূহ দেখাচ্ছে।
বর্গাকার তলগুলোকে ঘনকের পৃষ্ঠতল বলে। ঘনকের তলগুলো পরস্পর সর্বসম বর্গক্ষেত্র। অতএব ঘনকের পরস্পর সর্বসম ছয়টি বর্গাকার পৃষ্ঠতল থাকে। প্রতিটি তল ও তার সন্নিহিত তল পরস্পর লম্ব। তলগুলো পরস্পর মিলিত হওয়ার ফলে একাধিক ধার ও শীর্ষ উৎপন্ন হয়। তিনটি ধার পরস্পর যে বিন্দুতে মিলিত হয়, ঐ বিন্দুকে শীর্ষ বলে।
সুতরাং, একটি ঘনকের যা থাকেঃ
- ৬টি বর্গাকার সর্বসম পৃষ্ঠতল
- ১২টি সমান দৈর্ঘ্যের ধার
- ৮টি শীর্ষ
ঘনক একটি বিশেষ ধরণের আয়তাকার ঘনবস্তু কারণ এটি অনেকগুলো আয়তাকার ঘনবস্তুর বৈশিষ্ট্য বহন করে।
তাই ঘনককে বেশকিছু আয়তাকার ঘনবস্তু হিসাবে অভিহিত করা যায়। একটি ঘনক যেসব আয়তাকার ঘনবস্তু ব’লে পরিচিত তা হলো -
- একটি নিয়মিত বহুতলক (a regular polyhedron)
- একটি সমবাহু আয়তাকার ঘনবস্তু (an equilateral cuboid)
- a regular hexahedron
- a right rhombohedron
- একটি সুষম বহুতলক (a uniform polyhedron)
- a square parallelepiped
- a trigonal trapezohedron
- সুষম বর্গীয় প্রিজম (a square prism)
- একটি প্লেটনিক সলিড (one of the platonic solids)
ঘনক উদাহরণ

ঘনকের ক্ষেত্রফল
একটি ঘনক ছয়টি বর্গাকার পৃষ্ঠতল দ্বারা গঠিত। আবার বর্গাকার তলগুলো পরস্পর সর্বসম। অতএব ঘনকের দৈর্ঘ্য, প্রস্থ ও উচ্চতা পরস্পর সমান।

ঘনকের ক্ষেত্রফলের একাধিকভাবে প্রতিপাদন করা যায়। নিচে ঘনকের ক্ষেত্রফল নির্ণয়ের সূত্র প্রতিপাদন করে দেখানো হলো:
প্রথম পদ্ধতি
মনে করি, একটি ঘনকের প্রত্যেক ধারের দৈর্ঘ্য a.
জানা আছে, আয়তাকার ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল = ২(ab + bc + ca) বর্গএকক
যেহেতু ঘনক একটি আয়তাকার ঘনবস্তু, অতএব দৈর্ঘ্য = প্রস্থ = উচ্চতা
অর্থাৎ, a = b = c বসাই,
∴ ঘনকের সমগ্রতলের ক্ষেত্রফল A হলে,
A = ২(ab + bc + ca) বর্গএকক
বা, A = ২(a.a + a.a + a.a) বর্গএকক
বা, A = ২(a2 + a2 + a2) বর্গএকক
বা, A = ২.৩a2 বর্গএকক
∴ A = ৬a2 বর্গএকক
দ্বিতীয় পদ্ধতি
একটি ঘনকের পৃষ্ঠতল ছয়টি এবং প্রতিটি তল বর্গাকার ও পরস্পর সর্বসম।
মনে করি, একটি বর্গাকার তলের ধারের দৈর্ঘ্য a.
∴ বর্গাকার ১টি তলের ক্ষেত্রফল = a2 বর্গএকক
যেহেতু ঘনকের ৬টি বর্গাকার সর্বসম তল থাকে, তাই ঘনকের সমগ্রতলের ক্ষেত্রফল হবে এর ৬টি তলের সমষ্টি।
∴ ঘনকের ক্ষেত্রফল A হলে, ঘনকের তলের ক্ষেত্রফলের সূত্র হবে
A = a2 + a2 + a2 + a2 + a2 + a2 বর্গএকক
∴ A = ৬a2 বর্গএকক
ঘনকের প্রত্যেক ধারের দৈর্ঘ্য a একক এবং সমগ্রতলের ক্ষেত্রফল A হলে,
A = ৬a2 বর্গএকক
ঘনকের আয়তন
ঘনকের ভূমির ক্ষেত্রফলকে উচ্চতা দিয়ে গুণ করলে আয়তন পাওয়া যায়।
প্রথম পদ্ধতি
মনে করি, একটি ঘনকের ধারের দৈর্ঘ্য a.
∴ একটি ঘনকের ভূমির ক্ষেত্রফল a.a = a2 বর্গএকক
∴ ঘনকের আয়তন = (ভূমির ক্ষেত্রফল × উচ্চতা) ঘনএকক
বা, ঘনকের আয়তন = a2.a ঘনএকক
∴ ঘনকের আয়তন = a3 ঘনএকক
দ্বিতীয় পদ্ধতি
মনে করি, একটি আয়তাকার ঘনবস্তুর দৈর্ঘ্য a, প্রস্থ b এবং উচ্চতা c.
∴ আয়তাকার ঘনবস্তুর আয়তন = abc ঘনএকক
এখন, ঘনক একটি আয়তাকার ঘনবস্তু, তাই এর দৈর্ঘ্য = প্রস্থ = উচ্চতা
অর্থাৎ, a = b = c বসাই,
∴ ঘনকের আয়তন =a.a.a ঘনএকক
∴ ঘনকের আয়তন = a3 ঘনএকক
ঘনকের আয়তন = (দৈর্ঘ্য × দৈর্ঘ্য × দৈর্ঘ্য) ঘন একক
ঘনকের প্রত্যেক ধারের দৈর্ঘ্য a একক এবং আয়তন V হলে,
V = a3 ঘনএকক
ঘনকের কর্ণের দৈর্ঘ্য
প্রথম পদ্ধতি
প্রথমে ঘনকের নিচের পৃষ্ঠতলের কর্ণ নির্ণয় করি।
নিচের বর্গাকার তলের বাহুর দৈর্ঘ্য a, a এবং কর্ণ দ্বারা যে ত্রিভুজ গঠিত হয়েছে তা একটি সমকোণী ত্রিভুজ।
ঘনকের ধারের দৈর্ঘ্য a এবং নিচের তলের কর্ণ k হলে,
k2 = a2 + a2
বা, k2 = ২a2
বা, k = √২a2
∴ k = a√২
চিত্রে, ঘনকের কর্ণ হলো d.
আবার a, d এবং a√২ বাহু তিনটি দ্বারা যে ত্রিভুজ গঠিত হয়েছে তা একটি সমকোণী ত্রিভুজ যার অতিভুজ হলো d.
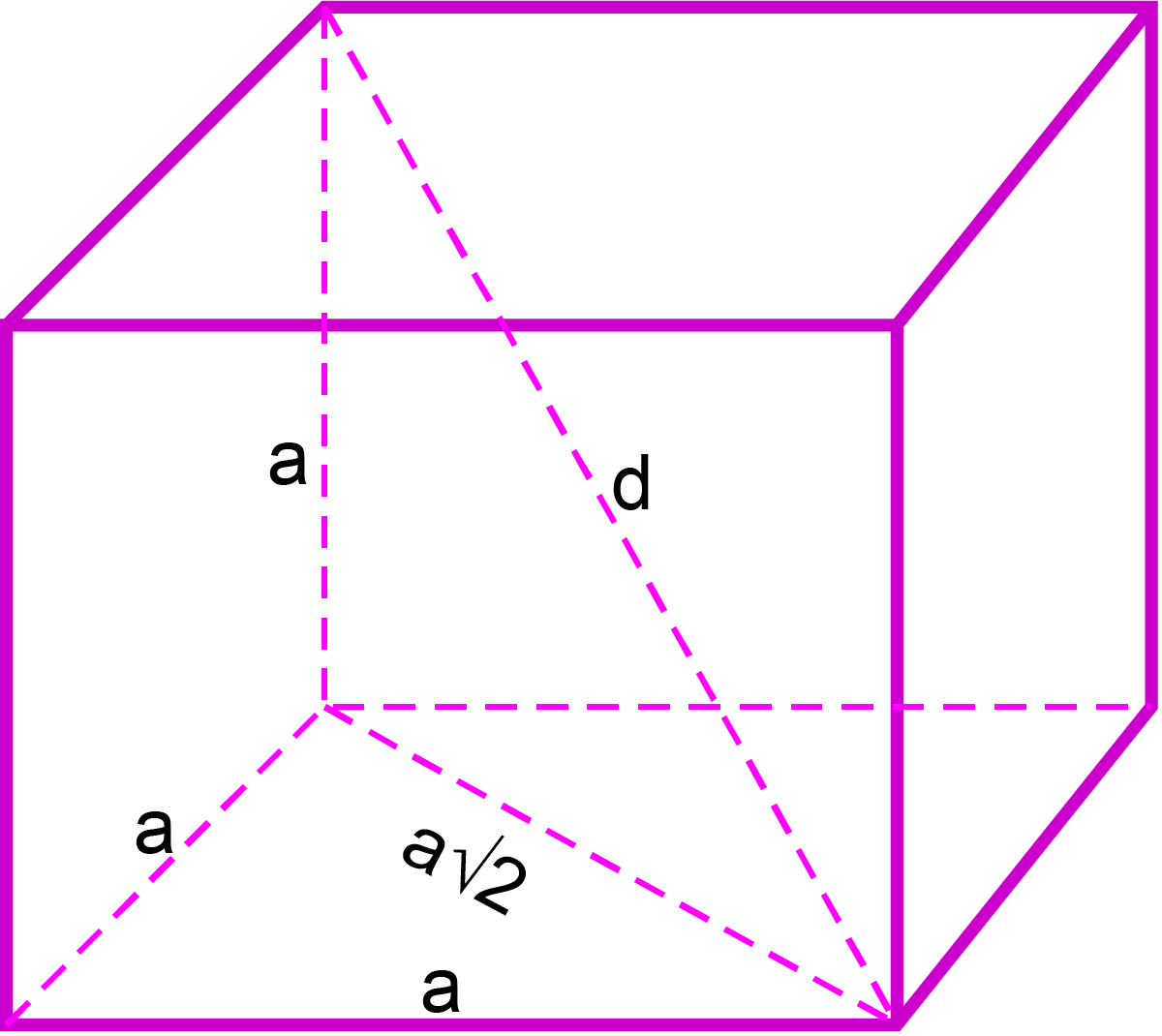
পিথাগোরাসের উপপাদ্য অনুসারে,
d2 = a2 + (a√২)2
বা, d2 = a2 + ২a2
বা, d2 = ৩a2
বা, d = √৩a2
∴ d = a√৩
দ্বিতীয় পদ্ধতি
আয়তাকার ঘনবস্তুর দৈর্ঘ্য a, প্রস্থ b, উচ্চতা c এবং একটি কর্ণ d হলে,
d = √a2 + b2 + c2
যেহেতু ঘনক একটি আয়তাকার ঘনবস্তু, তাই এর দৈর্ঘ্য = প্রস্থ = উচ্চতা
অর্থাৎ, ঘনকের ক্ষেত্রে a = b = c
∴ ঘনকের কর্ণের দৈর্ঘ্য d হলে,
d = √a2 + a2 + a2
বা, d = √৩a2
∴ d = a√৩
ঘনকের ধারের দৈর্ঘ্য a একক এবং একটি কর্ণ d হলে,
d = a√৩ একক