বিষমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র

বিষমবাহু ত্রিভুজ

যে ত্রিভুজের বাহুগুলো পরস্পর অসমান তাকে বিষমবাহু ত্রিভুজ বলে।

অন্যভাবে বলা যায় ...

ত্রিভুজের কোণগুলো পরস্পর অসমান হলে তাকে বিষমবাহু ত্রিভুজ বলে।

সমতল জ্যামিতির অন্তর্গত ব্যাসিক জ্যামিতি চিত্রের অন্যতম একটি হলো ত্রিভুজ। আর সব ত্রিভুজের সাধারণ রূপ হলো বিষমবাহু ত্রিভুজ। অর্থাৎ, এই ত্রিভুজ সকল ত্রিভুজকে প্রতিনিধিত্ব করে।

বিষমবাহু ত্রিভুজের পরিসীমার সূত্র

বিষমবাহু ত্রিভুজের সবগুলো বাহুর সমষ্টিকে তার পরিসীমা বলে।

মনে করি, △ABC এর BC = a, AC = b এবং AB = c.

তাহলে পরিসীমা, 2s = a+b+c

বিষমবাহু ত্রিভুজ উদাহরণ

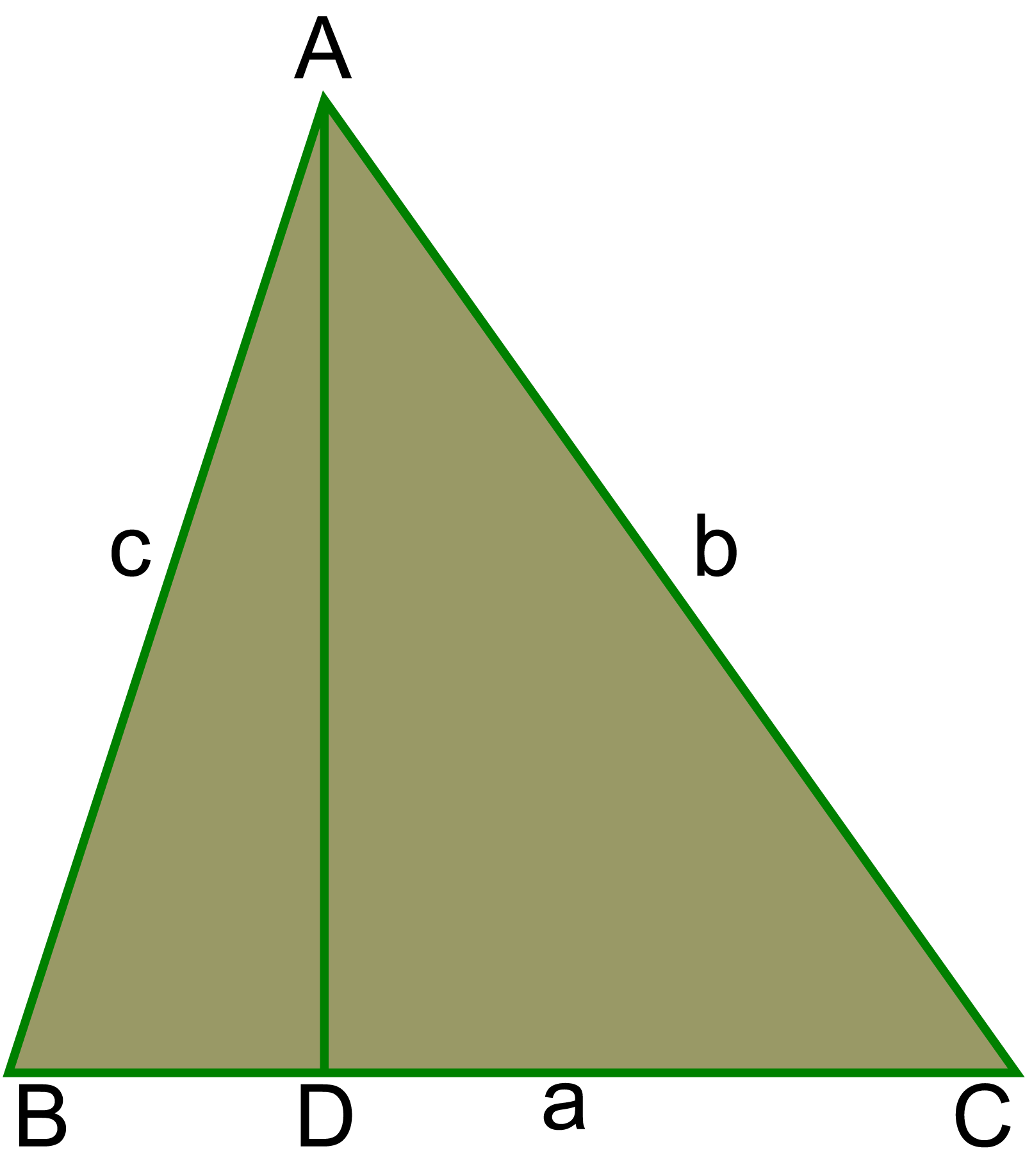
বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র

মনে করি, △ABC এর BC = a, AC = b এবং AB = c.

তাহলে পরিসীমা, 2s = a + b + c

AD⊥BC আঁকি। মনে করি, BD = x.

∴ CD = a-x.

সমকোণী △ABD এবং △ACD হতে লিখা যায় যথাক্রমে,

AD² = AB²-BD² ...... (1)

AD² = AC²-CD² ..... (2)

(1) ও (2) নং হতে লিখা যায়,

AB² - BD² = AC² - CD²

বা, c² - x² = b² - (a-x)²

বা, c² - x² = b² - a² + 2ax - x²

বা, 2ax = c² + a² - b²

বা, x = c² + a² - b²2a

আবার, AD² = c² - x²

বা, AD² = (c + x)(c - x)

বা, AD² = (c + c² + a² - b²2a ) (c - c² + a² - b²2a )

বা, AD² = (2ac + c² + a² - b²2a ) (2ac - c² - a² + b²2a )

বা, AD² = { (c + a)² - b² } { b² - (c - a)² }4a²

বা, AD² = (c + a + b) (c + a - b) (b + c - a) (b - c + a)4a²

বা, AD² = (a + b + c) (a + b + c - 2b) (a + b + c - 2a) (a + b + c - 2c)4a²

বা, AD² = 2s (2s - 2b) (2s - 2a) (2s - 2c)4a²

বা, AD² = 2 . 2 . 2 . 2s (s - b) (s - a) (s - c)4a²

বা, AD² = 4s (s - a) (s - b) (s - c)a²

বা, AD = √4s (s - a) (s - b) (s - c)√a²

বা, AD = 2a √s (s - a) (s - b) (s - c)

∴△ABC = 12 BC.AD

বা, △ABC = 12 a. 2a √s (s - a) (s - b) (s - c)

∴ △ABC = √s (s - a) (s - b) (s - c)

বিষমবাহু ত্রিভুজের বৈশিষ্ট্য

বিষমবাহু ত্রিভুজ একটি সাধারণ ত্রিভুজ বলে এর কতকগুলো সাধারণ বৈশিষ্ট্য রয়েছে। নিচে বিষমবাহু ত্রিভুজের কিছু বৈশিষ্ট্যসমূহ উল্লেখ করা হলো:

1. বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য পরস্পর অসমান।
2. বিষমবাহু ত্রিভুজের মধ্যমা তিনটির দৈর্ঘ্য পরস্পর অসমান।
3. বিষমবাহু ত্রিভুজের কোণ তিনটি পরস্পর সমান নয়।
4. বিষমবাহু ত্রিভুজের ভরকেন্দ্র থেকে বাহুত্রয়ের উপর অঙ্কিত লম্ব তিনটির দৈর্ঘ্য পরস্পর অসমান।
5. এই ত্রিভুজের শীর্ষ বিন্দু তিনটি থেকে এর বিপরীত বাহু তিনটির উপর অঙ্কিত লম্ব তিনটি পরস্পর সমান নয়।
6. বিষমবাহু ত্রিভুজের বহিঃবৃত্ত তিনটি পরস্পর অসমান।
7. এই ত্রিভুজের অন্তঃকেন্দ্র থেকে এর বাহুগুলোর উপর অঙ্কিত লম্বত্রয় পরস্পর সমান।