সিলিন্ডার বা বেলন কাকে বলে এবং সিলিন্ডারের ক্ষেত্রফল
এই টিউটোরিয়ালটি শেষে -
বেলন বা সিলিন্ডার কি তা বলতে পারা যাবে।
বেলনের ক্ষেত্রফল বা সিলিন্ডারের ক্ষেত্রফল এর সূত্র উদ্ভাবন করতে পারা যাবে।
বেলনের আয়তন বা সিলিন্ডারের আয়তন ব্যাখ্যা করতে পারা যাবে।
বেলনের সূত্র বা সিলিন্ডারের সূত্র বিশ্লেষণ করতে পারা যাবে।
বেলন বা সিলিন্ডার
যে ঘনবস্তুর ভূমি তল দুইটি পরস্পর সমান্তরাল ও সর্বসম দুইটি বৃত্ত এবং যার আবদ্ধ বক্রতল বিশিষ্ট গাত্র (body) এমন সকল বিন্দু দিয়ে গঠিত যে সকল বিন্দু একটি নির্দিষ্ট রেখাংশ থেকে সমদূরবর্তী।

সমদূরবর্তী বলতে বুঝায় একটি নির্দিষ্ট রেখাংশ হতে ঐ সকল বিন্দুর দুরত্ব একটি ধ্রূবক। নির্দিষ্ট রেখাংশ হলো ভূমি তল বৃত্ত দুইটির কেন্দ্রদ্বয়ের সংযোজক রেখাংশ। এই রেখাংশকে বেলন বা সিলিন্ডারের অক্ষ-রেখা বলে। আর অক্ষ-রেখার দৈর্ঘ্যকে বেলন বা সিলিন্ডারের উচ্চতা বলে।
বেলন বা সিলিন্ডার একটি ত্রিমাত্রিক বক্রাকার ঘনবস্তু যার ভূমি তল দুইটি পরস্পর সমান্তরাল সর্বসম বৃত্ত।
সিলিন্ডার উদাহরণ
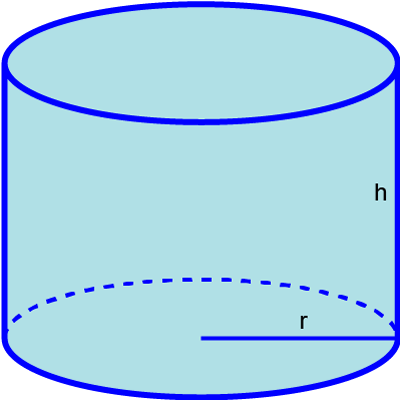
সিলিন্ডারের ভূমি
সিলিন্ডারের উপরিতল ও নিচের তল দুইটি বৃত্ত। আবার এই বৃত্তদ্বয় পরস্পর সমান্তরাল ও সর্বসম অর্থাৎ তল দুইটির ক্ষেত্রফল সমান। এই তলকে সিলিন্ডারের ভূমি বলে।
সিলিন্ডারের অক্ষ-রেখা
সিলিন্ডারের বৃত্তাকার ভূমিদ্বয়ের কেন্দ্রদ্বয়ের সংযোজক রেখাংশকে সিলিন্ডারের অক্ষ-রেখা বলে। আবার এই রেখাংশের দৈর্ঘ্য সিলিন্ডারের উচ্চতা সমান।
সিলিন্ডারের উচ্চতা
সিলিন্ডারের ভূমি তল দুইটির মধ্যবর্তী লম্ব দুরত্বকে সিলিন্ডারের উচ্চতা বলে। এই উচ্চতা সিলিন্ডারের অক্ষ-রেখার দৈর্ঘ্যের সমান। সিলিন্ডার বিষয়ক গাণিতিক সমস্যা যেমন সিলিন্ডারের বক্রতলের ক্ষেত্রফল, সিলিন্ডারের ক্ষেত্রফল, সিলিন্ডারের আয়তন ইত্যাদি নির্ণয় করার সময় সিলিন্ডারের উচ্চতার গুরুত্ব অনেক।
সিলিন্ডারের ভূমির ব্যাসার্ধ
সিলিন্ডারের ভূমি তল দুইটি সমান ক্ষেত্রফল বিশিষ্ট বৃত্ত। এই বৃত্তের ব্যাসার্ধকে সিলিন্ডারের ভূমির ব্যাসার্ধ বলে।
সিলিন্ডারের সূত্র
সাধারণভাবে, সিলিন্ডারের যেসব গাণিতিক সূত্র সচরাচর ব্যবহার ক’রে গাণিতিক সমস্যার সমাধান করা হয় - তা নিচে দেওয়া হলো।
সিলিন্ডারের ক্ষেত্রফল
সিলিন্ডারের ক্ষেত্রফল বলতে বুঝায় সিলিন্ডারের সমগ্রতলের ক্ষেত্রফল। তাহলে প্রথমে জানা দরকার সিলিন্ডারের অংশ কয়টি ও কী কী? দুইটি ভূমি তল ও একটি বক্রতল নিয়ে একটি সিলিন্ডার গঠিত হয়। অতএব, দুইটি ভূমি তল ও একটি বক্রতলের ক্ষেত্রফল নির্ণয় করে তাদের সমষ্টি করলেই সিলিন্ডারের ক্ষেত্রফল পাওয়া যায়।
সিলিন্ডারের ভূমির ক্ষেত্রফল
সিলিন্ডারের উপরিতল ও নিচের তল দুইটি ভূমি তল বলে পরিচিত। এই তল দুইটি বৃত্তাকার। আবার এই বৃত্তদ্বয়ের ক্ষেত্রফল সমান। যেহেতু ভূমি একটি বৃত্ত, তাই এর একটি ব্যাসার্ধ আছে।
সিলিন্ডারের ভূমির ক্ষেত্রফলের সূত্র
মনে করি, সিলিন্ডারের ভূমির ব্যাসার্ধ r. আবার এটি একটি বৃত্তক্ষেত্র হওয়ায়, এর ক্ষেত্রফল πr2 বর্গ একক। সিলিন্ডারের এরূপ দুইটি ভূমি তল রয়েছে।
ভূমি তল দুইটির ক্ষেত্রফলদ্বয়ের সমষ্টি Abase হলে,
Abase = πr2 + πr2
∴ Abase = 2πr2
সিলিন্ডারের ভূমির ব্যাসার্ধ r এবং ভূমি তল দুইটির ক্ষেত্রফলদ্বয়ের সমষ্টি Abase হলে,
Abase = 2πr2
সিলিন্ডারের বক্রতলের ক্ষেত্রফল
সিলিন্ডারের বক্রতলের ক্ষেত্রফল হলো এর বাঁকা (round) অংশের ক্ষেত্রফল অর্থাৎ যে তল বক্র হয়ে গোলাকার বা পাইপ আকার ধারণ করে। প্রথমে ভূমি তল দুইটিকে কেটে আলাদা করি। তাহলে গোলাকার পাইপের দুইদিকে ফাঁকা হয়ে গেল। এই গোলাকার পাইপের চারদিকে একটি সুতা দিয়ে একবার পেঁচিয়ে পরিমাপ করলে সুতার যে দৈর্ঘ্য পাওয়া যায় তা ভূমি তল বৃত্তের পরিধি 2πr এর সমান। এবার ফাঁকা পাইপটিকে লম্ব বরাবর কাটলে একটি আয়তক্ষেত্র উৎপন্ন হয় যার দৈর্ঘ্য 2πr এবং প্রস্থ সিলিন্ডারের উচ্চতা h এর সমান।
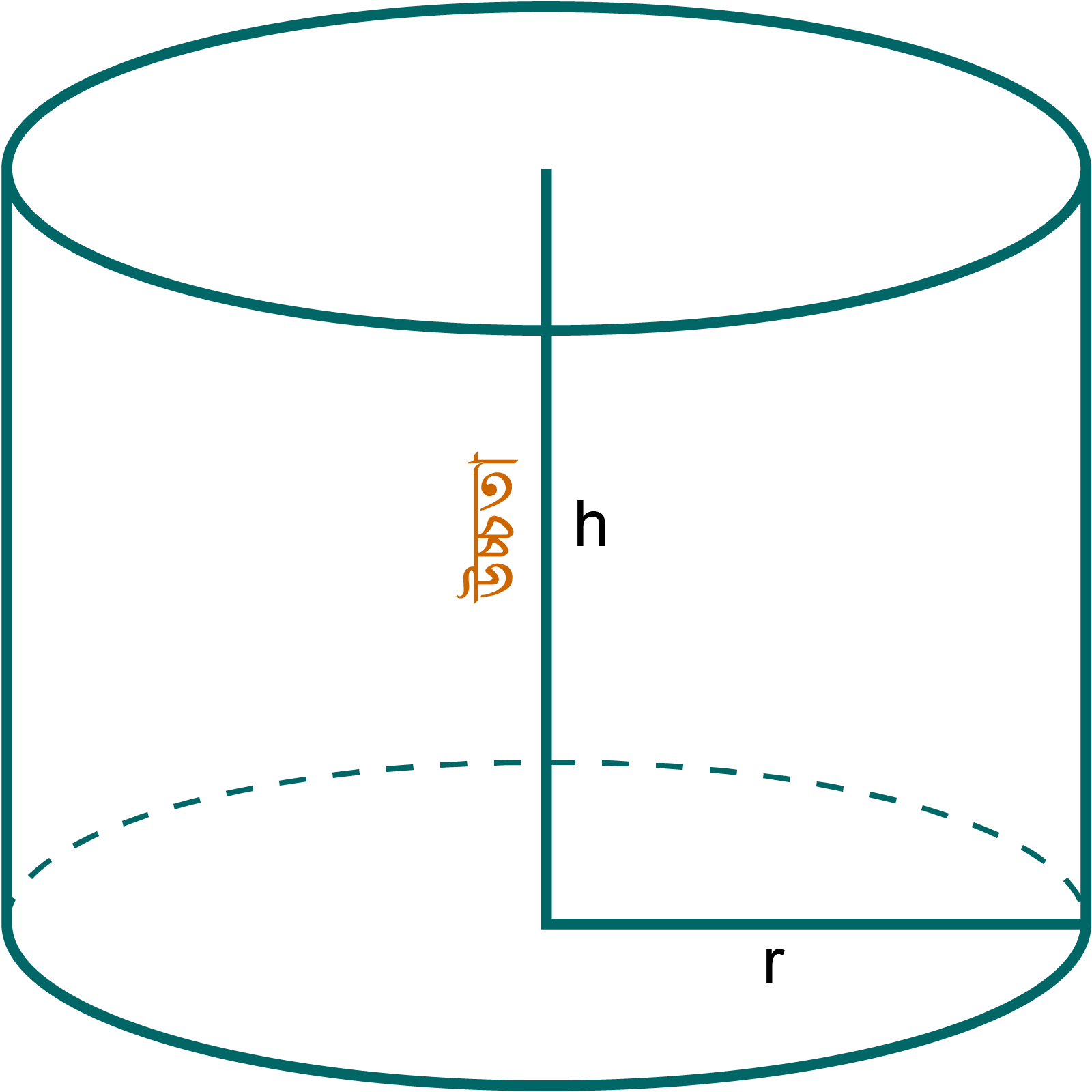
বেলনের বক্রতলের ক্ষেত্রফলের সূত্র
∴ সিলিন্ডারের বক্রতলের ক্ষেত্রফল = উপরোক্ত আয়তক্ষেত্রের ক্ষেত্রফল।
বা, সিলিন্ডারের বক্রতলের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গএকক
বা, সিলিন্ডারের বক্রতলের ক্ষেত্রফল =(২πr × h) বর্গএকক
∴ সিলিন্ডারের বক্রতলের ক্ষেত্রফল = (২πrh) বর্গএকক
সিলিন্ডারের ভূমির ব্যাসার্ধ r, উচ্চতা h এবং বক্রতলের ক্ষেত্রফল Acurved হলে,
Acurved = ২πrh বর্গএকক
সিলিন্ডারের সূত্র
∴ সিলিন্ডারের সমগ্রতলের ক্ষেত্রফল = সিলিন্ডারের ভূমির ক্ষেত্রফল + সিলিন্ডারের বক্রতলের ক্ষেত্রফল
অতএব, সিলিন্ডারের সমগ্রতলের ক্ষেত্রফল A, সিলিন্ডারের ভূমির ক্ষেত্রফল Abase এবং সিলিন্ডারের বক্রতলের ক্ষেত্রফল Acurved হলে,
A = Abase + Acurved
বা, A = (২πr2+২πrh) বর্গএকক
∴ A = ২πr(r+h) বর্গএকক
সিলিন্ডারের ভূমির ব্যাসার্ধ r, উচ্চতা h এবং সমগ্রতলের ক্ষেত্রফল A হলে,
A = ২πr(r+h) বর্গএকক
সিলিন্ডারের আয়তন
যে কোন সুষম ঘনবস্তুর ভূমির ক্ষেত্রফলকে তার উচ্চতা দিয়ে গুণ করলে আয়তন পাওয়া যায়। সিলিন্ডার একটি সুষম ঘনবস্তু। তাই, সিলিন্ডারের ভূমির ক্ষেত্রফলকে উচ্চতা দিয়ে গুণ করলে আয়তন পাওয়া যায়।
সিলিন্ডারের আয়তনের সূত্র
মনেকরি, সিলিন্ডারের ভূমির ব্যাসার্ধ r এবং উচ্চতা h.
সুতরাং, সিলিন্ডারের ভূমির ক্ষেত্রফল =π r2 বর্গএকক
∴ সিলিন্ডারের আয়তন = (ভূমির ক্ষেত্রফল × উচ্চতা) ঘনএকক
অতএব, সিলিন্ডারের ভূমির ক্ষেত্রফল Abase, উচ্চতা h এবং আয়তন V হলে,
V = Abase × h
∴ V = πr2h ঘনএকক
সিলিন্ডারের ভূমির ব্যাসার্ধ r, উচ্চতা h এবং আয়তন V হলে,
V = πr2h ঘনএকক