একটি বৃত্তের কয়টি অংশ থাকে
এই টিউটোরিয়ালটি শেষে ...
একটি বৃত্তের কয়টি অংশ থাকে তা বর্ণনা করতে পারা যাবে।
বৃত্তের বিভিন্ন অংশ চিত্র সহ ব্যাখ্যা করতে পারা যাবে।
বৃত্ত বিষয়ক জ্যামিতিক ধারণাগুলো সম্পর্কে পরিপূর্ণ জ্ঞান লাভ করতে হলে একটি বৃত্তের কয়টি অংশ থাকে তা ভালভাবে দরকার। বৃত্তের অংশ বলতে এর কেন্দ্র, ব্যাসার্ধ, ব্যাস, জ্যা, পরিধি, বৃত্তচাপ, বৃত্তকলা ইত্যাদিকে বুঝায়। মূলত; বৃত্ত একটি সুষম আবদ্ধ বক্ররেখা। প্রথমে বৃত্তের বিভিন্ন অংশ চিত্রের মাধ্যমে চিহ্নিত করা; অতপর এর প্রত্যেকটি অংশকে ভাষার মাধ্যমে কিভাবে প্রকাশ করা যায় তা শেখা জরুরী।
একটি বৃত্তের বিভিন্ন অংশের পরিচিতি ও তাদের বৈশিষ্ট্য সম্পর্কে সঠিক জ্ঞান থাকলে বৃত্ত বিষয়ক জ্যামিতিক সমস্যাগুলোর সমাধান খুব সহজে করা যায়। বৃত্ত হলো সমতলে অবস্থিত সুষম আবদ্ধ বক্রাকার চিত্র। একটি বৃত্তের কয়টি অংশ থাকে তার মোটামুটি একটি তালিকা নিচে তুলে ধরা হলো।
- কেন্দ্র
- ব্যাসার্ধ
- ব্যাস
- জ্যা
- স্পর্শক
- বৃত্তচাপ
- উপচাপ
- অধিচাপ
- অর্ধবৃত্তচাপ
- ছেদক রেখা
- বৃত্তকলা
- বৃত্তাংশ
- পরিধি
- ক্ষেত্রফল
- কেন্দ্রস্থ কোণ
- বৃত্তস্থ কোণ
- বৃত্তের অভ্যন্তর
- বৃত্তের বহির্ভাগ
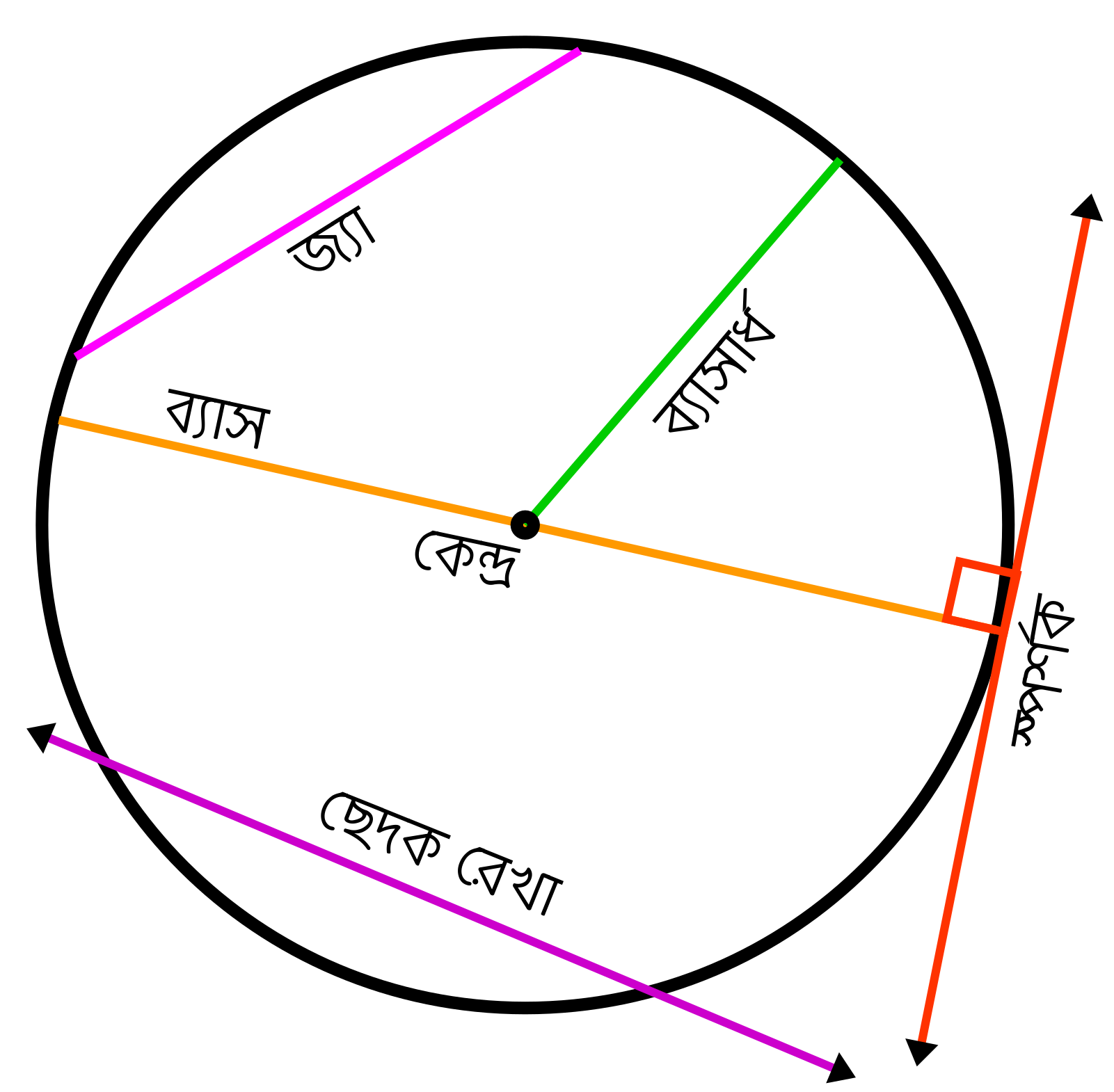
চিত্রে, বৃত্তের বিভিন্ন উপাদানসমূহ ও তাদের অবস্থান দেখা যাচ্ছে।
বৃত্তের কেন্দ্র
যে নির্দিষ্ট বিন্দু থেকে বৃত্তের পরিধির উপর অবস্থিত সকল বিন্দুর দুরত্ব সমান, ঐ নির্দিষ্ট বিন্দুকে বৃত্তের কেন্দ্র বলে। একটি বৃত্তের কেবল একটি মাত্র কেন্দ্র থাকে। তাই বৃত্তের কেন্দ্র একটি অনন্য বিন্দু। একটি নিদির্ষ্ট বিন্দু একাধিক বৃত্তের কেন্দ্র হতে পারে। অর্থাৎ, একটি কেন্দ্র দিয়ে একাধিক বৃত্ত অংকন করা যায়। কিন্তু একটি বৃত্তের একাধিক কেন্দ্র থাকতে পারে না। বৃত্তের ব্যাসার্ধ বৃত্তের কেন্দ্রগামী একটি রেখাংশ। আবার, বৃত্তের ব্যাসও বৃত্তের কেন্দ্রগামী একটি রেখাংশ।
নিচের বিষয়গুলো একটি বৃত্তের কেন্দ্রের জন্য সত্য:
- একটি বৃত্তের একটি ও কেবল একটি মাত্র কেন্দ্র থাকে।
- কেন্দ্র হলো একটি বৃত্তের ব্যাসের মধ্যবিন্দু।
- একটি কেন্দ্র দিয়ে অসংখ্য বৃত্ত অংকন করা যায়।
- একটি বৃত্তের দুইটি ব্যাস পরস্পর কেন্দ্র বিন্দুতে ছেদ করে।
বৃত্তের ব্যাসার্ধ
বৃত্তের কেন্দ্র হতে পরিধি পর্যন্ত দূরত্বকে ব্যাসার্ধ বলে। অন্যভাবে বললে, বৃত্তের কেন্দ্র থেকে পরিধির উপর যে কোন বিন্দুর দূরত্বকে বৃত্তের ব্যাসার্ধ বলে। অর্থাৎ, বৃত্তের কেন্দ্র ও পরিধির উপর যে কোন বিন্দুর সংযোজক রেখাংশ হলো বৃত্তের ব্যাসার্ধ। একটি বৃত্তের যে কয়টি অংশ থাকে তার মধ্যে সবচেয়ে মৌলিক একটি অংশ হলো ব্যাসার্ধ। একটি বৃত্তে অসংখ্য ব্যাসার্ধ আঁকা যায়।
বৃত্তের ব্যাসার্ধ হলো ব্যাসের অর্ধেক।
∴ ব্যাসার্ধ = ব্যাস ÷ ২
বৃত্তের ব্যাসার্ধ = ব্যাস ÷ ২
নিচের বিষয়গুলো একটি বৃত্তের ব্যাসার্ধের জন্য সত্য:
- একটি বৃত্তে অসংখ্য ব্যাসার্ধ আঁকা যায়।
- বৃত্তের সকল ব্যাসার্ধের দৈর্ঘ্য পরস্পর সমান।
- বৃত্তের ব্যাসার্ধ হলো ব্যাসের অর্ধেক।
- একটি বৃত্তের ব্যাসার্ধ জানা থাকলে বৃত্তটি আঁকা যায়।
বৃত্তের ব্যাস
বৃত্তের কেন্দ্রগামী জ্যা কে বৃত্তের ব্যাস বলে। অন্যভাবে বললে, বৃত্তের জ্যা কেন্দ্রগামী হলে তাকে বৃত্তের ব্যাস বলে।
বৃত্তের কেন্দ্র দিয়ে অতিক্রমকারী রেখাংশের প্রান্তবিন্দুদ্বয় বৃত্তের পরিধির উপর অবস্থিত হলে, ঐ রেখাংশকে বৃত্তের ব্যাস বলে। বৃত্তের কেন্দ্র বৃত্তের ব্যাসের মধ্যবিন্দু। আবার বৃত্তের ব্যাস বৃত্তের একটি জ্যা বটে। তবে এটি একটি বিশেষ জ্যা। বৃত্তের ব্যাস বা এই বিশেষ জ্যা বৃত্তের কেন্দ্র দিয়ে যায়। বৃত্তের ব্যাসই বৃহত্তম জ্যা। একটি বৃত্তে অসংখ্য ব্যাস আঁকা যায়।
বৃত্তের ব্যাস বৃত্তের ব্যাসার্ধের দ্বিগুণ।
∴ ব্যাস = ২ ⨯ ব্যাসার্ধ
বৃত্তের ব্যাস = ২ ⨯ ব্যাসার্ধ
নিচের বিষয়গুলো একটি বৃত্তের ব্যাসের জন্য সত্য:
- একটি বৃত্তে অসংখ্য ব্যাস আঁকা যায়।
- বৃত্তের সকল ব্যাসের দৈর্ঘ্য পরস্পর সমান।
- বৃত্তের ব্যাস হলো ব্যাসার্ধের দ্বিগুণ।
- একটি বৃত্তের ব্যাসের দৈর্ঘ্য জানা থাকলে বৃত্তটি অংকন করা যায়।
- বৃত্তের ব্যাস হলো বৃত্তের বৃহত্তম জ্যা।
বৃত্তের ক্ষেত্রফল
বৃত্তের ব্যাসার্ধের বর্গকে π দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়। এখন প্রশ্ন হলো π কি? বৃত্তের পরিধি ও ব্যাসের অনুপাত হলো π. একটি বৃত্তের ব্যাস ৭ একক হলে তার পরিধি হয় ২২ একক।
∴ বৃত্তের পরিধি : বৃত্তের ব্যাস = ২২ : ৭
অর্থাৎ, π = ২২৭।
একটি বৃত্তের ব্যাসার্ধ r একক হলে এর ক্ষেত্রফল πr2 বর্গ একক।
∴ বৃত্তের ক্ষেত্রফল = πr2 বর্গ একক।
একটি বৃত্তের ব্যাসার্ধ r একক হলে এর ক্ষেত্রফল = πr2 বর্গ একক।
নিচের বিষয়গুলো একটি বৃত্তের ক্ষেত্রফলের জন্য সত্য:
- বৃত্তের ক্ষেত্রফল হলো ব্যাসার্ধের বর্গের π গুণ।
- বৃত্তের ব্যাসার্ধের দৈর্ঘ্য জানা থাকলে ক্ষেত্রফল নির্ণয় করা যায়।
- বৃত্তের ব্যাসের দৈর্ঘ্য জানা থাকলে ক্ষেত্রফল নির্ণয় করা যায়।
বৃত্তের জ্যা
বৃত্তের পরিধির উপর যেকোনো দুইটি বিন্দুর সংযোজক রেখাংশকে বৃত্তের জ্যা বলে। এরূপ দুইটি বিন্দু যোগ করে অসংখ্য রেখাংশ অঙ্কন করা যায়। তাই একটি বৃত্তের অসংখ্য জ্যা থাকতে পারে।
বৃত্তের ব্যাসই হচ্ছে বৃত্তের বৃহত্তম জ্যা। বৃত্তের যে কয়টি অংশ থাকে জ্যা হলো তাদের মধ্যে অন্যতম একটি। আবার, বৃত্তের যে কোন জ্যা এর লম্ব সমদ্বিখণ্ডক কেন্দ্রগামী। তাছাড়া, যেকোনো বৃত্তের সমান সমান জ্যা কেন্দ্র হতে সমদূরবর্তী। বৃত্তের জ্যা এর আরেকটি অন্যতম বৈশিষ্ট্য হলো বৃত্তের দুটি জ্যা এর মধ্যে কেন্দ্রের নিকটতর জ্যাটি অপর জ্যা অপেক্ষা বৃহত্তর।
নিচের বিষয়গুলো একটি বৃত্তের জ্যা এর জন্য সত্য:
- একটি বৃত্তে অসংখ্য জ্যা আঁকা যায়।
- বৃত্তের যে কোনো জ্যা এর লম্বসমদ্বিখণ্ডক কেন্দ্রগামী।
- বৃত্তের কেন্দ্র থেকে সমদুরবর্তী সকল জ্যা পরস্পর সমান।
- বৃত্তের বৃহত্তম জ্যা হলো ব্যাস।
- বৃত্তের সমান সমান জ্যা কেন্দ্র হতে সমদূরবর্তী।
বৃত্তের স্পর্শক
একটি সরলরেখা যদি একটি বৃত্তকে একটি ও কেবল একটি মাত্র বিন্দুতে ছেদ করে তাহলে ঐ সরলরেখাটিকে বৃত্তের স্পর্শক বলে। অন্যভাবে বললে, একটি সরলরেখা ও একটি বৃত্ত যদি একটি ও কেবল একটি বিন্দুতে ছেদ করে তাহলে সরলরেখাটিকে বৃত্তের স্পর্শক বলে।
বৃত্তের একটি অনন্য বিন্দুতে স্পর্শকারী, ব্যাসের উপর লম্ব সরলরেখাকে বৃত্তের স্পর্শক বলে। অতএব, বৃত্তের স্পর্শক বৃত্তের একটি অনন্য বিন্দুতে স্পর্শ করে। স্পর্শক সবসময়ই বৃত্তের ব্যাস বা ব্যাসার্ধের উপর লম্ব এবং বৃত্তের পরিধির উপর একটি মাত্র বিন্দু দিয়ে অতিক্রম করে।
বৃত্তের উপরস্থ কোনো বিন্দুতে বৃত্তে কেবল একটি স্পর্শক আঁকা যায়। আবার, বৃত্তের বহিঃস্থ কোনো বিন্দু হতে ঐ বৃত্তে সর্বোচ্চ দুইটি স্পর্শক আঁকা যায়। তাছাড়া, বৃত্তের কোনো বিন্দুতে অঙ্কিত স্পর্শক স্পর্শবিন্দুগামী ব্যাসার্ধের উপর লম্ব।
নিচের বিষয়গুলো একটি বৃত্তের স্পর্শকের জন্য সত্য:
- একটি বৃত্তে অসংখ্য স্পর্শক আঁকা যায়।
- একটি স্পর্শক বৃত্তের ব্যাসার্ধর উপর লম্ব।
- বৃত্তের একটি বিন্দুতে একটি ও কেবল একটি স্পর্শক আঁকা যায়।
- বৃত্তের বহিঃস্থ কোনো বিন্দু হতে ঐ বৃত্তে সর্বোচ্চ দুইটি স্পর্শক অংকন করা যায়।
- যেকোনো স্পর্শক বৃত্তকে একটি ও কেবল একটি বিন্দুতে ছেদ করে।
বৃত্তের পরিধি
একটি বৃত্তের কেন্দ্র হতে সমান দূরত্ব বজায় রেখে কোন বিন্দুর চলার পথের দৈর্ঘ্যকে বৃত্তের পরিধি বলে।
বৃত্তের সীমান্ত বরাবর দৈর্ঘ্যকে বৃত্তের পরিধি বলে। অতএব বৃত্তের পরিধি হলো বৃত্তের পরিসীমা। বৃত্তের ব্যাস বা ব্যাসার্ধ জানা থাকলে পরিধি নির্ণয় করা যায়। বৃত্তের ব্যাসকে π দ্বারা গুণ করলে গুণ করলে পরিধি পাওয়া যায়। একটি বৃত্তের ব্যাসার্ধ r একক হলে এর পরিধি 2πr একক।
∴ বৃত্তের পরিধি = 2πr একক।
একটি বৃত্তের ব্যাসার্ধ r একক হলে
বৃত্তের পরিধি = 2πr একক।
নিচের বিষয়গুলো একটি বৃত্তের পরিধির জন্য সত্য:
- বৃত্তের পরিধির উপর অসংখ্য বিন্দু থাকে।
- বৃত্তের কেন্দ্র থেকে পরিধির উপর সকল বিন্দুর দুরত্ব পরস্পর সমান।
- বৃত্তের ব্যাসার্ধের দৈর্ঘ্য জানা থাকলে পরিধি নির্ণয় করা যায়।
- বৃত্তের ব্যাসের দৈর্ঘ্য জানা থাকলে পরিধি নির্ণয় করা যায়।
- বৃত্তের ক্ষেত্রফল জানা থাকলে পরিধি নির্ণয় করা যায়।
বৃত্তের ছেদক রেখা
যে সরলরেখা বৃত্তকে দুইটি বিন্দুতে ছেদ করে তাকে বৃত্তের ছেদক রেখা বলে। অতএব, একটি জ্যা কে উভয়দিকে সীমাহীনভাবে বর্ধিত করলে ছেদক রেখা উৎপন্ন হয় যা বৃত্তকে দুইটি বিন্দুতে ছেদ করে।
বৃত্তচাপ
বৃত্তের পরিধির যেকোনো অংশকে বৃত্তচাপ বলে। বৃত্ত চাপের প্রান্তবিন্দুদ্বয় যদি কোন রেখাংশের প্রান্তবিন্দুদ্বয় হয়, তাহলে ঐ রেখাংশকে বৃত্তের জ্যা বলে। বৃত্তচাপ হলো বৃত্তের ক্ষেত্রফলের একটি অংশ। একটি বৃত্তের যে কয়টি অংশ থাকে তাদের মধ্যে একটি অংশ হলো বৃত্তচাপ।
বৃত্তের একই চাপের উপর দণ্ডায়মান বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক। বিপরীতক্রমে, বৃত্তের একই চাপের উপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ। আবার, অর্ধবৃত্তস্থ কোণ এক সমকোণ বা ৯০°।

নিচের বিষয়গুলো একটি বৃত্তের বৃত্তচাপের জন্য সত্য:
- একটি বৃত্তে অসংখ্য বৃত্তচাপ উৎপন্ন হতে পারে।
- বৃত্তের ব্যাস বৃত্তের পরিধিকে পরস্পর সমান দুইটি বৃত্তচাপে বিভক্ত করে।
- বৃত্তচাপ দ্বারা কেন্দ্রে উৎপন্ন কোণকে কেন্দ্রস্থ কোণ বলে।
- বৃত্তচাপ দ্বারা পরিধিতে উৎপন্ন কোণকে বৃত্তস্থ কোণ বলে।
অর্ধ বৃত্তচাপ বা অর্ধবৃত্ত
যে বৃত্তচাপের দৈর্ঘ্য পরিধির অর্ধেক তাকে অর্ধ বৃত্তচাপ বা অর্ধবৃত্ত বলে।
বৃত্তাংশ
বৃত্তের একটি জ্যা ও একটি চাপ দ্বারা গঠিত অঞ্চলকে বৃত্তাংশ বলে।
বৃত্ত কলা
বৃত্তের দুইটি ব্যাসার্ধ ও একটি চাপ দ্বারা গঠিত অঞ্চলকে বৃত্তকলা বা বৃত্তীয় ক্ষেত্র বলে।