দৈর্ঘ্য কাকে বলে - দৈর্ঘ্য নির্ণয়ের সূত্র
এই টিউটোরিয়ালটি শেষে -
দৈর্ঘ্য কাকে বলে তা বর্ণনা করতে পারা যাবে।
দৈর্ঘ্য নির্ণয়ের সূত্র কি তা ব্যাখ্যা করতে পারা যাবে।
দৈর্ঘ্য পরিমাপের একক কি তা বলতে পারা যাবে।
দৈর্ঘ্য প্রস্থ উচ্চতা কাকে বলে তা তুলনামূলক বিশ্লেষণ করতে পারা যাবে।
দৈনন্দিন জীবনে দৈর্ঘ্য প্রস্থ সূত্র প্রয়োগ করতে পারা যাবে।
দৈর্ঘ্য
দুরত্বের পরিমাপকে দৈর্ঘ্য বলে। সাধারণভাবে বললে, কোনো বস্তুর বৃহত্তম মাত্রা হলো দৈর্ঘ্য। উদাহরণস্বরূপ বলা যায়, একটি আয়তক্ষেত্রের বৃহত্তম মাত্রাকে দৈর্ঘ্য বলে এবং ক্ষুদ্রতম মাত্রাকে প্রস্থ বলে।

আবার একটি ইটের বৃহত্তম মাত্রা ২৪ সেন্টিমিটার। তাই বলা হয়, ইটটির দৈর্ঘ্য ২৪ সেন্টিমিটার। আন্তর্জাতিক পরিমাপ পদ্ধতি অনুযায়ী, মাত্রার দুরত্বের পরিমাণই হলো দৈর্ঘ্য। অতএব, বস্তুর মাত্রার পরিমাপকই হলো দৈর্ঘ্য।
অন্যভাবে বলা যায়, জগতে কোনো বস্তুর এক প্রান্ত থেকে অন্য প্রান্তের সরল রৈখিক দুরত্ব বা পরিমাপকে দৈর্ঘ্য বলে। এখানে জগত বলতে ত্রিমাত্রিক জগতকেই বুঝানো হচ্ছে।
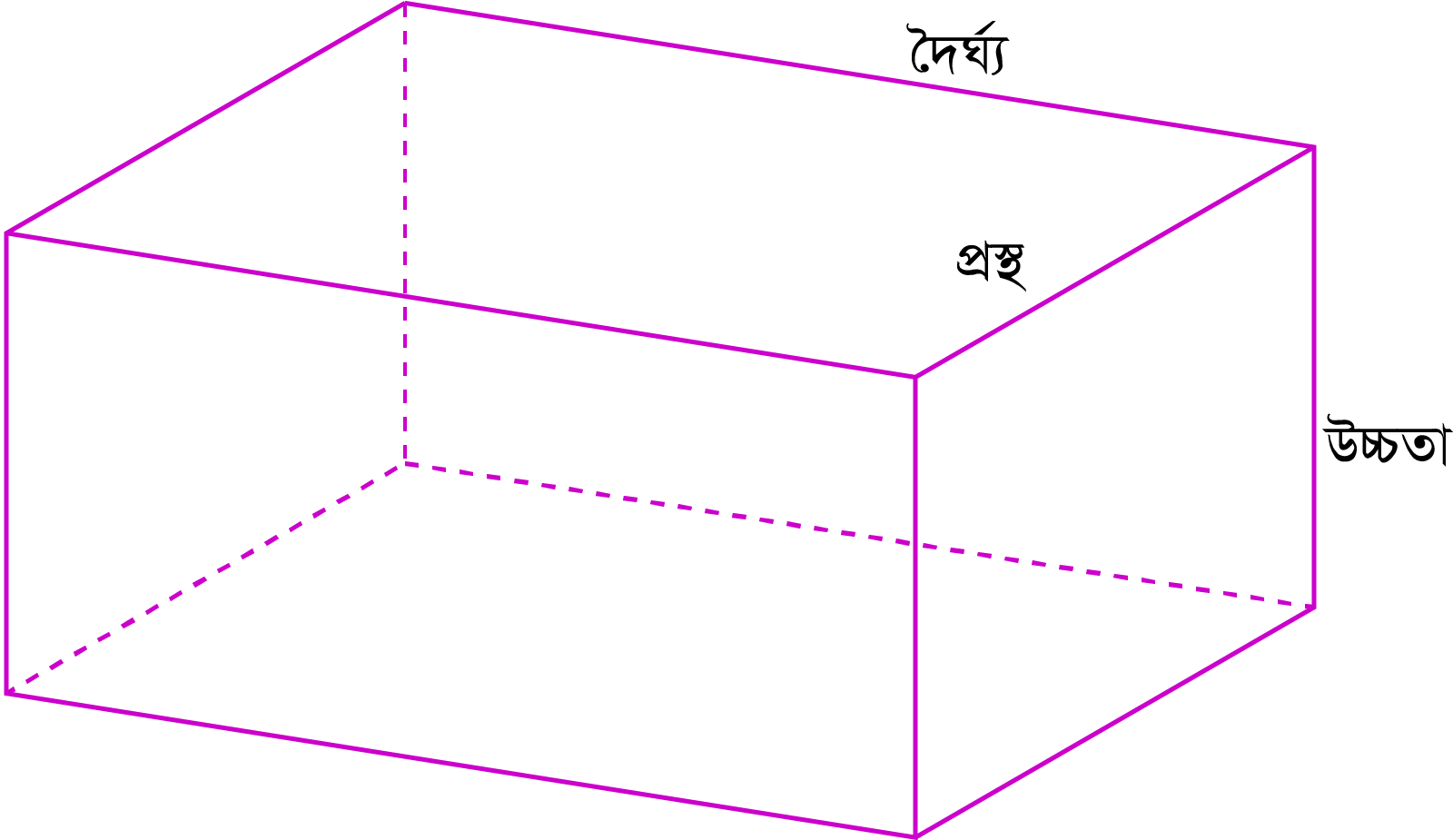
দৈর্ঘ্য, প্রস্থ ও উচ্চতা - এরা সবাই ভিন্ন ভিন্ন দুরত্বকে প্রতিনিধিত্ব করে। তাই এদের প্রত্যেকটিকে এক-একটি দৈর্ঘ্য বলা যেতে পারে। তবে ত্রিমাত্রিক জগতে দৈর্ঘ্যকে প্রস্থ এবং উচ্চতা থেকে আলাদা করা যায়।
দৈর্ঘ্য কেবল একটি মাত্রার দুরত্বকে পরিমাপ করে। অর্থাৎ একটি মাত্রার পরিমাপকের নাম দৈর্ঘ্য। তাই দৈর্ঘ্যের মাত্রা এক। অতএব, দৈর্ঘ্য একমাত্রিক জ্যামিতির অন্তর্গত। দৈর্ঘ্য যেমন একটিমাত্র মাত্রাকে পরিমাপ করে, ক্ষেত্রফল তেমনি দুইটি মাত্রা - দৈর্ঘ্য ও প্রস্থকে পরিমাপ করে। তাই ক্ষেত্রফল দ্বিমাত্রিক জ্যামিতির অন্তর্ভূক্ত। আবার, আয়তন তিনটি মাত্রা - দৈর্ঘ্য, প্রস্থ ও উচ্চতাকে পরিমাপ করে। তাই ত্রিমাত্রিক জ্যামিতি আয়তন নিয়ে আলোচনা করে। অতএব, আয়তন ত্রিমাত্রিক জ্যামিতির সাথে সম্পৃক্ত।
দৈর্ঘ্য নির্ণয়ের সূত্র
দৈর্ঘ্য শুধু একটি মাত্রাকে প্রতিনিধিত্ব করে। কিন্তু একটি আয়তাকার তলের ক্ষেত্রফল তার দৈর্ঘ্য ও প্রস্থের সাথে সম্পৃক্ত। এ ধরণের তলের দৈর্ঘ্যকে প্রস্থ দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়। তাই যে কোনো তলের ক্ষেত্রফল দ্বিমাত্রিক জ্যামিতির সাথে জড়িত। তলের মাত্রা দুইটি হলো দৈর্ঘ্য ও প্রস্থ। একটি আয়তক্ষেত্র বা আয়তাকার পৃষ্ঠতলের দৈর্ঘ্য ও প্রস্থের গুণফলই হলো তার ক্ষেত্রফলের পরিমাপ। ফলে ক্ষেত্রফলকে প্রস্থ দ্বারা ভাগ করলে দৈর্ঘ্য পাওয়া যায়। অতএব, আয়তাকার পৃষ্ঠতলের ক্ষেত্রফলের সূত্রটি দাঁড়ায়,
আয়তাকার পৃষ্ঠতলের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক।
∴ দৈর্ঘ্য = (আয়তাকার পৃষ্ঠতলের ক্ষেত্রফল ÷ প্রস্থ) একক।
আয়তাকার পৃষ্ঠতলের দৈর্ঘ্য নির্ণয়ের সূত্র
দৈর্ঘ্য = (আয়তাকার পৃষ্ঠতলের ক্ষেত্রফল ÷ প্রস্থ) একক
প্রস্থ
দৈর্ঘ্যের এক প্রান্ত থেকে একই সমতলে অবস্থিত এবং সমকোণে আনত অপর একটি প্রান্তের সরল রৈখিক দুরত্বের পরিমাপকে প্রস্থ বলে। যেমন - বইয়ের একটি পৃষ্ঠা নিয়ে বিশ্লেষণ করা যেতে পারে। পৃষ্ঠাটির বৃহত্তম মাত্রা বা ধার হলো দৈর্ঘ্য। লক্ষ্যণীয়, বৃহত্তম মাত্রা ও ক্ষুদ্রতম মাত্রা দুইটি একই সমতলে অবস্থিত। আবার, ক্ষুদ্রতম ধারটি বৃহত্তম ধারের সাথে ৯০০ বা সমকোণে আনত। তাছাড়া, এই ক্ষুদ্র্রতম ধারটি হলো বৃহত্তম ধারের এক প্রান্ত থেকে সমকোণে আনত ক্ষুদ্রতম ধারের অপর প্রান্তের রৈখিক দুরত্ব। তাই পৃষ্ঠাটির ক্ষুদ্রতম ধারটি হলো প্রস্থ।
ত্রিমাত্রিক বস্তুর সাহায্যেও প্রস্থ ব্যাখ্যা করা যেতে পারে। উদাহরণস্বরূপ, একটি ঘরের মেঝের বৃহত্তম ধার হলো দৈর্ঘ্য এবং ক্ষুদ্রতম ধার হলো প্রস্থ। কারণ বৃহত্তর ধার ও ক্ষুদ্রতর ধার দুইটি একই সমতলে অবস্থিত। আবার, ক্ষুদ্রতর ধার ও বৃহত্তর ধারের মধ্যবর্তী কোণ ৯০০। তাছাড়া, ক্ষুদ্রতর ধারটি বৃহত্তর ধারের এক প্রান্ত থেকে সমকোণে আনত একটি সরলরেখিক দুরত্ব। অতএব, ক্ষুদ্রতর ধারটি হলো প্রস্থ।
আয়তাকার পৃষ্ঠতলের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক।
∴ প্রস্থ = (আয়তাকার পৃষ্ঠতলের ক্ষেত্রফল ÷ দৈর্ঘ্য) একক।
আয়তাকার পৃষ্ঠতলের প্রস্থ নির্ণয়ের সূত্র
প্রস্থ = (আয়তাকার পৃষ্ঠতলের ক্ষেত্রফল ÷ দৈর্ঘ্য) একক
দৈর্ঘ্য, প্রস্থ ও উচ্চতা - তুলনামূলক আলোচনা
দৈর্ঘ্য, প্রস্থ ও উচ্চতা - এদের প্রত্যকটি ভিন্ন ভিন্ন দুরত্বের পরিমাপক। তবে এরা দুরত্বের পরিমাপক হলেও এদেরকে আলাদা করে চিন্তা করা যায়। দ্বিমাত্রিক জগতে দৈর্ঘ্যকে প্রস্থ থেকে আলাদা করে ভাবলে, বৃহত্তর দুরত্বের মাত্রাকে দৈর্ঘ্য হিসাবে বিবেচনা করা হয়। আর দৈর্ঘ্যের সাথে ৯০০ কোণে আনত ক্ষুদ্রতর দুরত্বের মাত্রাকে প্রস্থ বলে।

এখানে উল্লেখ্য, কোনো দৈর্ঘ্যের কাছাকাছি অবস্থিত দৈর্ঘ্যের চেয়ে ক্ষুদ্রতর যেকোনো দুরত্ব হলেই তাকে কিন্তু প্রস্থ বলা যায় না। প্রস্থ হতে হলে ক্ষুদ্রতর দুরত্বটিকে অবশ্যই একই সমতলে অবস্থিত তাদের একটি সাধারণ প্রান্তবিন্দুতে দৈর্ঘ্যের সাথে পরস্পর লম্ব হতে হবে। তাহলে একটি নির্দিষ্ট দুরত্বকে প্রস্থ হতে হলে নিচের শর্তগুলো পূরণ করা আবশ্যকঃ
- নির্দিষ্ট দুরত্ব (প্রস্থ) -এর পরিমাপ দৈর্ঘ্য অপেক্ষা ছোট।
- দৈর্ঘ্য ও নির্দিষ্ট দুরত্ব (প্রস্থ) একই সমতলে অবস্থিত।
- দৈর্ঘ্য ও নির্দিষ্ট দুরত্ব (প্রস্থ) -এর একটি সাধারণ প্রান্ত থাকে।
- নির্দিষ্ট দুরত্ব (প্রস্থ) ও দৈর্ঘ্যের সাধারণ প্রান্তবিন্দুতে উৎপন্ন কোণের পরিমাপ এক সমকোণ।
আবার দৈর্ঘ্যকে উচ্চতা থেকে পৃথক করে ভাবা যেতে পারে। ত্রিমাত্রিক জগতে কোনো বস্তুর মাত্রা তিনটি হলো দৈর্ঘ্য, প্রস্থ ও উচ্চতা। ঘন জ্যামিতি এই মাত্রা তিনটিকে একত্রে আলোচনা করে। দৈর্ঘ্য যে তলে অবস্থিত, উচ্চতা অন্য আরেকটি তলে অবস্থিত। অর্থাৎ, দৈর্ঘ্যের তল এবং উচ্চতার তল দুইটি পরস্পর ভিন্ন তল। উচ্চতা হলো বস্তুর উলম্ব দুরত্ব। এজন্য, দৈর্ঘ্য ও উচ্চতা দুইটি ভিন্ন সমতলে অবস্থিত। ত্রিমাত্রিক জগতে কোনো বস্তুর যে ধার বা মাত্রা দৈর্ঘ্যের সাথে ৯০০ কোণে আনত ভিন্ন সমতলে অবস্থিত হয়, তাই উচ্চতা। তাহলে ঘনবস্তুর উচ্চতা হতে হলে নিচের শর্তগুলো পূরণ করা আবশ্যকঃ
- দৈর্ঘ্য ও উচ্চতার সমতল দুইটি ভিন্ন অর্থাৎ, দৈর্ঘ্য ও উচ্চতা পরস্পর দুইটি ভিন্ন সমতলে অবস্থিত।
- দৈর্ঘ্য ও উচ্চতার একটি সাধারণ প্রান্ত থাকে।
- উচ্চতা সাধারণ প্রান্তবিন্দুতে দৈর্ঘ্যের সাথে ৯০০ কোণে আনত।
দৈর্ঘ্য পরিমাপের একক
দৈর্ঘ্য বলতে মূলতঃ দুরত্বকেই বুঝানো হয়। দৈর্ঘ্যকে বিভিন্ন একক দ্বারা পরিমাপ করা হয়। প্রাচীনকাল থেকেই দৈর্ঘ্য পরিমাপের জন্য মানুষ বিভিন্ন ধরনের একক ব্যবহার করত। মানব দেহের বিভিন্ন অঙ্গকে দৈর্ঘ্য পরিমাপের একক হিসাবে ব্যবহার করত। যেমন হাতের দৈর্ঘ্য। আবার একটি নির্দিষ্ট দুরত্ব অতিক্রম করতে কত কদম ফেলতে হয় - এভাবে প্রতি কদমকে দৈর্ঘ্য পরিমাপের একক হিসাবে ব্যবহার করত। তাছাড়া দুইটি বিখ্যাত স্থানের মধ্যবর্তী পরস্পর দুরত্বকে বড় কোনো দৈর্ঘ্য পরিমাপের একক হিসাবে ব্যবহার করত। সভ্যতা বিকাশের সাথে সাথে দৈর্ঘ্য পরিমাপের এসব এককেরও পরিবর্তন হয়েছে। বর্তমানে আন্তর্জাতিক একক পদ্ধতি অনুযায়ী, দৈর্ঘ্য পরিমাপের জন্য যেসব একক ব্যবহার করা হয়, তাহলো মিটার, হেক্টোমিটার, কিলোমিটার, ডেসিমিটার, সেন্টিমিটার ইত্যাদি। আবার আলোকবর্ষ হলো জ্যোতির্বিদ্যায় ব্যবহৃত দৈর্ঘ্য পরিমাপের একক। তবে দৈর্ঘ্য পরিমাপের একক - মিলিমিটার, সেন্টিমিটার, ডেকামিটর, কিলোমিটার ইত্যাদি সবই দৈর্ঘ্য পরিমাপের এসব একক মিটার থেকে উৎপত্তি হয়েছে। তাই দৈর্ঘ্য পরিমাপের মূল একক মিটার। অর্থাৎ মিটার হলো দৈর্ঘ্য পরিমাপের ভিত্তি একক।