সমকোণী সমদ্বিবাহু ত্রিভুজ কাকে বলে

সমকোণী সমদ্বিবাহু ত্রিভুজ

যে ত্রিভুজ একইসাথে সমকোণী ত্রিভুজ ও সমদ্বিবাহু ত্রিভুজ তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে। অন্যভাবে বললে, যে সমকোণী ত্রিভুজের দুইটি বাহু পরস্পর সমান তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে। আবার, যে সমদ্বিবাহু ত্রিভুজের একটি কোণের পরিমাপ ৯০° বা সমকোণ তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।

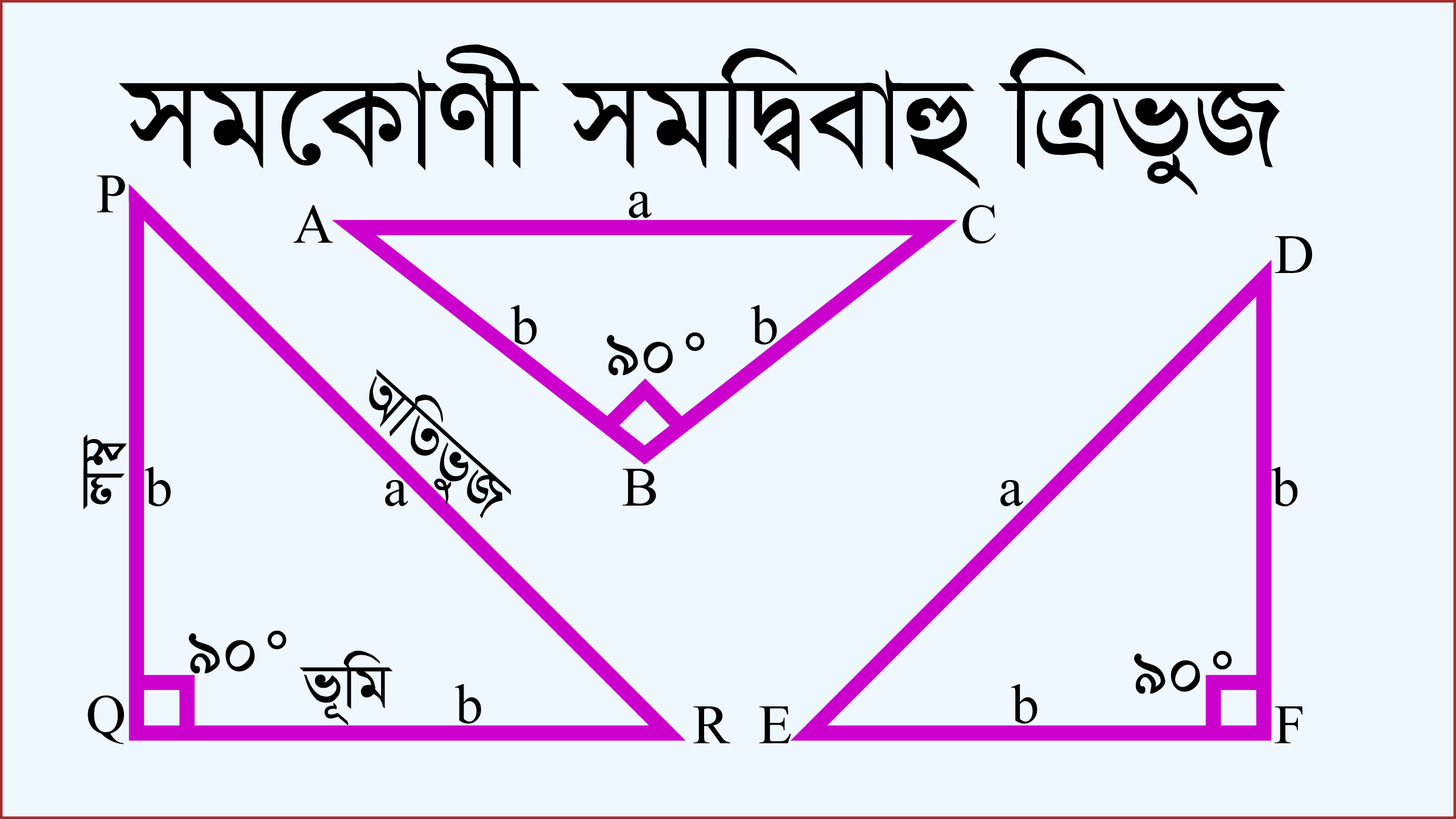
যে সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় পরস্পর সমান তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে। তাহলে সমকোণী সমদ্বিবাহু ত্রিভুজের পরিশীলিত সংজ্ঞা দাঁড়ায়,

যে ত্রিভুজের দুইটি বাহু পরস্পর সমান ও একটি কোণ সমকোণ তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।

সমকোণী সমদ্বিবাহু ত্রিভুজের দুইটি বাহু পরস্পর সমান বলে সমান সমান বাহুর বিপরীত কোণ দুইটিও পরস্পর সমান। এই ত্রিভুজের সমকোণ ছাড়া অপর কোণ দুইটির সমষ্টি এক সমকোণ বা ৯০°। আবার কোণ দুইটি পরস্পর সমান বলে প্রত্যেকটি কোণের পরিমাপ ৪৫°।

সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটির নাম ভূমি ও লম্ব। আর সমকোণ সংলগ্ন বাহুদ্বয় সমান হওয়ার কারণে সমকোণী সমদ্বিবাহু ত্রিভুজের লম্ব ও ভূমি পরস্পর সমান। সমকোণী সমদ্বিবাহু ত্রিভুজ একদিকে সমকোণী ত্রিভুজকে প্রতিনিধিত্ব করে; অন্যদিকে এই ত্রিভুজ সমদ্বিবাহু ত্রিভুজকেও প্রতিনিধিত্ব করে। সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ বলে। আর এই অতিভুজই সমকোণী সমদ্বিবাহু ত্রিভুজের বৃহত্তম বাহু।

সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র

যে সূত্র প্রয়োগ করে সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয় করা হয় তাকে সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র বলে। সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়ের গুণফলের অর্ধেককে সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল বলে। সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটি পরস্পর সমান অর্থাৎ, ভূমি ও লম্ব পরস্পর সমান।

∴ সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল = (১২ ⨯ ভূমি ⨯ লম্ব) বর্গ একক।

অর্থাৎ, সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল = (১২ ⨯ ভূমি ⨯ ভূমি) বর্গ একক।

∴ সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল = ১২ ⨯ (ভূমি)^২ বর্গ একক।

অথবা, সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল = ১২ ⨯ (লম্ব)^২ বর্গ একক।

তাই বলা যায়, সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়ের যেকোনো একটির বর্গকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়।

একটি সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন সমান সমান বাহুদ্বয়ের দৈর্ঘ্য a একক হলে,

সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল = 12 ⨯ a² বর্গ একক।

সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র

যে সূত্র প্রয়োগ করে সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা নির্ণয় করা হয় তাকে সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র বলে। সমকোণী সমদ্বিবাহু ত্রিভুজের বাহুগুলোর সমষ্টিকে সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা বলে।

∴ সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা = (অতিভুজ + লম্ব + ভূমি) একক।
সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় ভূমি ও লম্ব পরস্পর সমান।
∴ সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা = (অতিভুজ + লম্ব + লম্ব) একক।
∴ সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র = (অতিভুজ + ২ ⨯ লম্ব) একক।

সুতরাং, সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভুজ ও সমকোণ সংলগ্ন যেকোনো একটি বাহুর দ্বিগুণের সমষ্টিকে সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা বলে।

আবার যেহেতু সমকোণী সমদ্বিবাহু ত্রিভুজের লম্ব ও ভূমি পরস্পর সমান, অতএব সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র নিম্নরূপেও লিখা যায়।
সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা = (অতিভুজ + ২⨯ ভূমি) একক।

সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভুজ a একক এবং সমকোণ সংলগ্ন বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য b একক হলে
সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র = (a + 2b) একক

সমকোণী সমদ্বিবাহু ত্রিভুজ সংক্রান্ত সচরাচর যেসব প্রশ্নসমূহ মানুষ করে থাকে।

যে ত্রিভুজের দুইটি বাহু পরস্পর সমান ও একটি কোণ সমকোণ বা ৯০° তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে। সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়ের নাম লম্ব ও ভূমি। এই ত্রিভুজের লম্ব ও ভূমির দৈর্ঘ্য পরস্পর সমান। সমকোণী সমদ্বিবাহু ত্রিভুজ একদিকে সমকোণী ত্রিভুজ এবং অন্যদিকে সমদ্বিবাহু ত্রিভুজ।

সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ সংলগ্ন যেকোনো একটি বাহুর বর্গকে ২ দ্বারা ভাগ করলে যে মান পাওয়া যায় তাকে সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল বলে।

সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র = ১২ ⨯ (লম্ব)^২ বর্গ একক।
অথবা, সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র = ১২ ⨯ (ভূমি)^২ বর্গ একক।

সমকোণী সমদ্বিবাহু ত্রিভুজের একটি কোণ সমকোণ হওয়ার কারণে একটি কোণের পরিমাপ ৯০°। আর অবশিষ্ট সূক্ষ্মকোণদ্বয়ের যোগফল ৯০°। আবার সমকোণী সমদ্বিবাহু ত্রিভুজের সূক্ষ্মকোণ দুইটি পরস্পর সমান হওয়ার কারণে তাদের প্রত্যেকটির পরিমাপ ৪৫°। তাহলে, একটি সমকোণী সমদ্বিবাহু ত্রিভুজের কোণ তিনটির পরিমাপ হলো ৯০°, ৪৫° ও ৪৫°।

সমকোণী সমদ্বিবাহু ত্রিভুজের তিনটি কোণের মান হলো ৪৫°, ৪৫° ও ৯০°। সুতরাং, সমকোণী সমদ্বিবাহু ত্রিভুজের তিনটি কোণের অনুপাত হলো ৪৫° : ৪৫° : ৯০°।
অর্থাৎ, সমকোণী সমদ্বিবাহু ত্রিভুজের তিনটি কোণের অনুপাত হলো ১ : ১ : ২ [সকল রাশিকে ৪৫° দ্বারা ভাগ করে]।
∴ সূক্ষ্মকোণ : সূক্ষ্মকোণ : সমকোণ = ১ : ১ : ২।
অথবা, সমকোণ : সূক্ষ্মকোণ : সূক্ষ্মকোণ = ২ : ১ : ১।

সমকোণী সমদ্বিবাহু ত্রিভুজ বিশ্লেষণ করলে কতকগুলো বৈশিষ্ট্য পরিলক্ষিত হয়। তিনটি সমকোণী সমদ্বিবাহু ত্রিভুজের বৈশিষ্ট্য নিচে দেওয়া হলো।

1. সমকোণী সমদ্বিবাহু ত্রিভুজের সমকোণ ছাড়া সূক্ষ্মকোণ দুইটি পরস্পর সমান এবং প্রত্যেকটির সূক্ষ্মকোণের পরিমাপ ৪৫°।
2. সমকোণী সমদ্বিবাহু ত্রিভুজের লম্ব ও ভূমির দৈর্ঘ্য পরস্পর সমান।
3. সমকোণী সমদ্বিবাহু ত্রিভুজের যেকোনো একটি বাহুর দৈর্ঘ্য জানা থাকলে অন্য দুই বাহুর দৈর্ঘ্য নির্ণয় করা যায়।