সমকোণী ত্রিভুজের বৈশিষ্ট্য

সমকোণী ত্রিভুজ বিশ্লেষণ একগুচ্ছ সমকোণী ত্রিভুজের বৈশিষ্ট্য পরিলক্ষিত হয়। এসব বৈশিষ্ট্য সমূহ সমকোণী ত্রিভুজের সংজ্ঞা ও সমকোণী ত্রিভুজের গঠন প্রণালী থেকে নিঃসৃত হয়। যেমন - সমকোণী ত্রিভুজের একটি কোণ সমকোণ বা ৯০°। সমকোণের বিপরীত বাহুকে অতিভুজ বলে। অতিভুজই সমকোণী ত্রিভুজের বৃহত্তম বাহু। আবার, সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটিকে ভূমি ও লম্ব বলে। তাছাড়া, যে সমকোণী ত্রিভুজের দুইটি বাহু পরস্পর সমান তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।

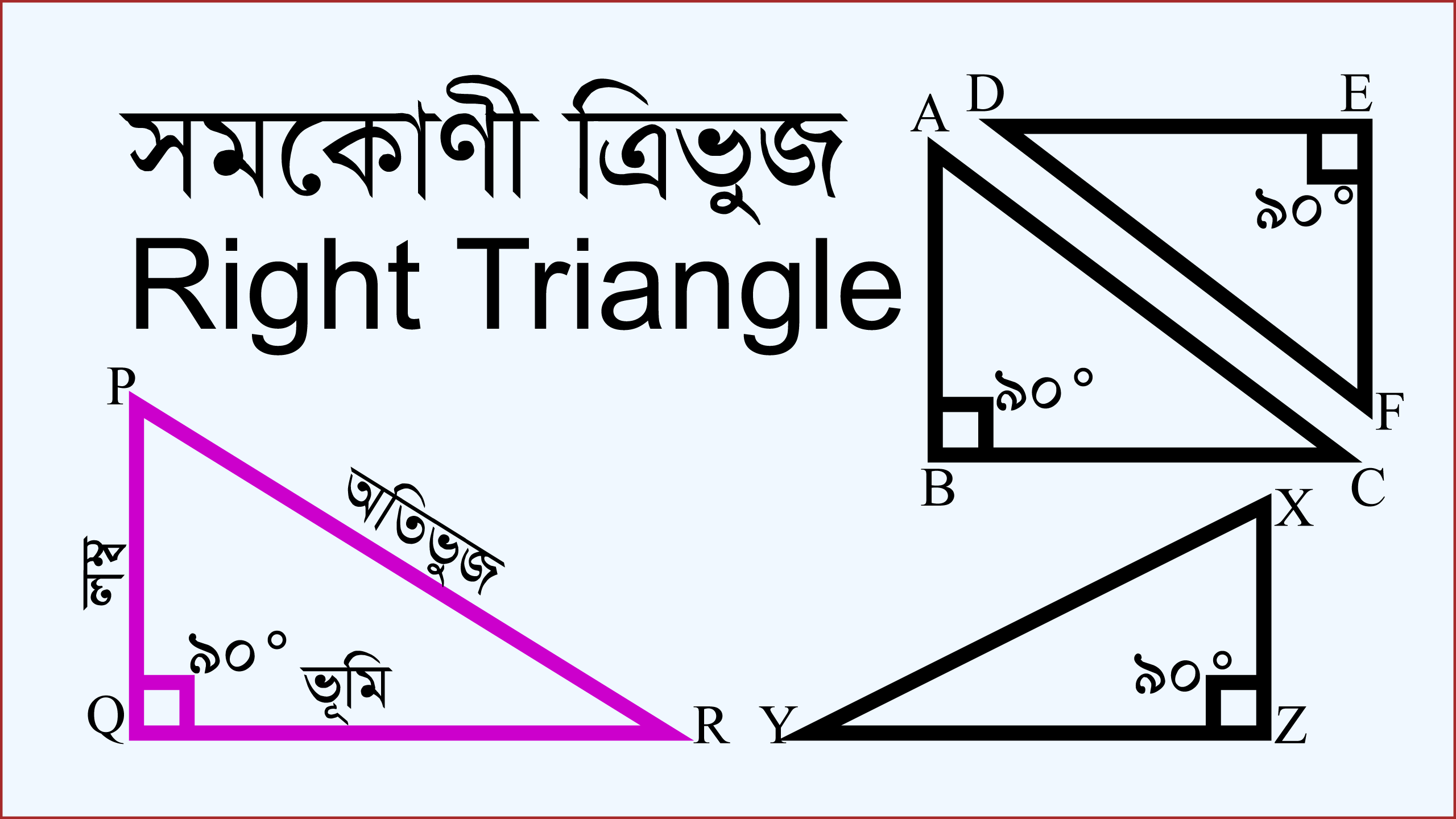
যাহোক, সমকোণী ত্রিভুজ সম্পর্কে সম্মক জ্ঞান লাভ করার জন্য সমকোণী ত্রিভুজ কাকে বলে এবং বৈশিষ্ট্য সমূহ জানা দরকার। নিচে একগুচ্ছ সমকোণী ত্রিভুজের বৈশিষ্ট্য ও সমকোণী সমদ্বিবাহু ত্রিভুজের বৈশিষ্ট্য সমূহ তুলে ধরা হলো।

• সমকোণী ত্রিভুজের একটি কোণ সমকোণ বা ৯০°।
• সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুর নাম হলো অতিভুজ।
• সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য পূর্ণসংখ্যা হলে ঐ সমকোণী ত্রিভুজকে ‘পিথাগোরীয় ত্রিভুজ’ বলে।
• সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয়ের গুণফলকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়।
• সমকোণী ত্রিভুজের সমকোণ ছাড়া অপর কোণ দুইটির প্রত্যেকটি এক-একটি সূক্ষ্মকোণ।
• সমকোণী সমদ্বিবাহু ত্রিভুজের সূক্ষ্মকোণদ্বয়ের প্রত্যেকটি পরিমাপ ৪৫°।
• সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল তার অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্র দুইটির ক্ষেত্রফলের সমষ্টির সমান।
• সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটির নাম ভূমি ও লম্ব।
• সমকোণী সমদ্বিবাহু ত্রিভুজের যেকোনো একটি বাহুর দৈর্ঘ্য দেওয়া থাকলে অপর বাহু দুইটির দৈর্ঘ্য নির্ণয় করা যায়।
• সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য পূর্ণসংখ্যা হলে ঐ বাহুগুলোর দৈর্ঘ্যকে একত্রে ‘পিথাগোরিয়ান ত্রিপল’(Pythagorean Triple) বা ‘পিথাগোরীয় ত্রয়’ বলা হয় এবং (a,b,c) আকারে লিখে প্রকাশ করা হয় যেখানে a,b ও c সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য। যেমন একটি সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য ৩, ৪, ৫ হলে তাকে (৩,৪,৫) লিখা হয়।
• এই ত্রিভুজের সমকোণ ব্যতীত অন্য দুইটি কোণের সমষ্টি ৯০°।
• সমকোণী ত্রিভুজের সমকৌণিক শীর্ষবিন্দু এবং অতিভুজের মধ্যবিন্দুর সংযোজক রেখাংশ দ্বারা ত্রিভুজটি যে দুইটি ত্রিভুজে বিভক্ত হয়, তারা উভয়ই সমদ্বিবাহু ত্রিভুজ।
• সমকোণী সমদ্বিবাহু ত্রিভুজের লম্ব ও ভূমি পরস্পর সমান।
• সমকোণী ত্রিভুজের অতিভুজই বৃহত্তম বাহু।
• সমকোণী ত্রিভুজের যেকোনো দুইটি বাহুর দৈর্ঘ্য জানা থাকলে তৃতীয় বাহুর দৈর্ঘ্য নির্ণয় করা যায়।
• সমকোণী ত্রিভুজই হলো পিথাগোরাসের উপপাদ্যের ভিত্তি।
• সমকোণী ত্রিভুজের শীর্ষবিন্দুত্রয় দিয়ে অতিক্রান্ত বৃত্ত অঙ্কন করলে ঐ বৃত্তের ব্যাস অতিভুজের সমান।
• এই ত্রিভুজের একটি কোণ ও কোণ সংলগ্ন একটি বাহু জানা থাকলে অন্য সবগুলো বাহু ও কোণগুলো নির্ণয় করা যায়।
• সমকোণী সমদ্বিবাহু ত্রিভুজ এর সমকোণ সংলগ্ন যেকোন বাহু ও অতিভুজের অনুপাত সবসময়ই ১:√২।
• সমকোণী ত্রিভুজের যেকোনো একটি সূক্ষ্মকোণের পরিমাপ জানা থাকলে অপর সূক্ষ্মকোণটির পরিমাপ নির্ণয় করা যায়।
• সমকোণী সমদ্বিবাহু ত্রিভুজ এর পা(legs) অর্থাৎ সমকোণ সংলগ্ন বাহু দুইটি পরস্পর সমান এবং অতিভুজ যেকোন একটি পা এর √২ গুণ।
• সমকোণী ত্রিভুজের সমকৌণিক শীর্ষ বিন্দু এবং অতিভুজের মধ্যবিন্দুর সংযোজক রেখাংশের দৈর্ঘ্য অতিভুজের অর্ধেক।
• সমকোণী ত্রিভুজের অতিভুজের সংলগ্ন কোণ দুইটির প্রত্যেকটি সূক্ষ্মকোণ।
• সমকোণী ত্রিভুজের সমকোণ ছাড়া অপর কোণদ্বয়ের একটি আরেকটির দ্বিগুণ হলে ক্ষুদ্রতম কোণের বিপরীত বাহুর দ্বিগুণ অতিভুজের সমান।
• সমকোণী ত্রিভুজের সমকৌণিক শীর্ষ থেকে অতিভুজের উপর লম্ব অঙ্কন করলে অতিভুজ যে দুইটি অংশে বিভক্ত হয় সেই অংশ দুইটি এবং সংশ্লিষ্ট অংশ সংবলিত ত্রিভুজ দুইটির ক্ষেত্রফলদ্বয় সমানুপাতিক।