রম্বস
এই টিউটোরিয়ালটি শেষে -
রম্বস ব্যাখ্যা করতে পারা যাবে।
রম্বসের সূত্র নির্ণয় করতে পারা যাবে।
রম্বসের পরিসীমা নির্ণয় করতে পারা যাবে।
রম্বসের কর্ণের সূত্র উদ্ভাবন করতে পারা যাবে।
রম্বসের বাহু ও কোণগুলোর মধ্যে সম্পর্ক ব্যাখ্যা করতে পারা যাবে।
যে চতুর্ভুজের চারটি বাহুর দৈর্ঘ্য পরস্পর সমান তাকে রম্বস বলে। অন্যভাবে বললে, যে চতুর্ভুজের সব বাহুর দৈর্ঘ্য সমান কিন্তু কোনো কোণই সমকোণ নয় তাকে রম্বস বলে। আরও কয়েকভাবে রম্বস এর সংজ্ঞা দেওয়া যায়। যেমন -
সামান্তরিকের সন্নিহিত বাহুদ্বয় পরস্পর সমান হলে তাকে রম্বস বলে।
রম্বস হলো বিশেষ ধরণের একটি চতুর্ভুজ।
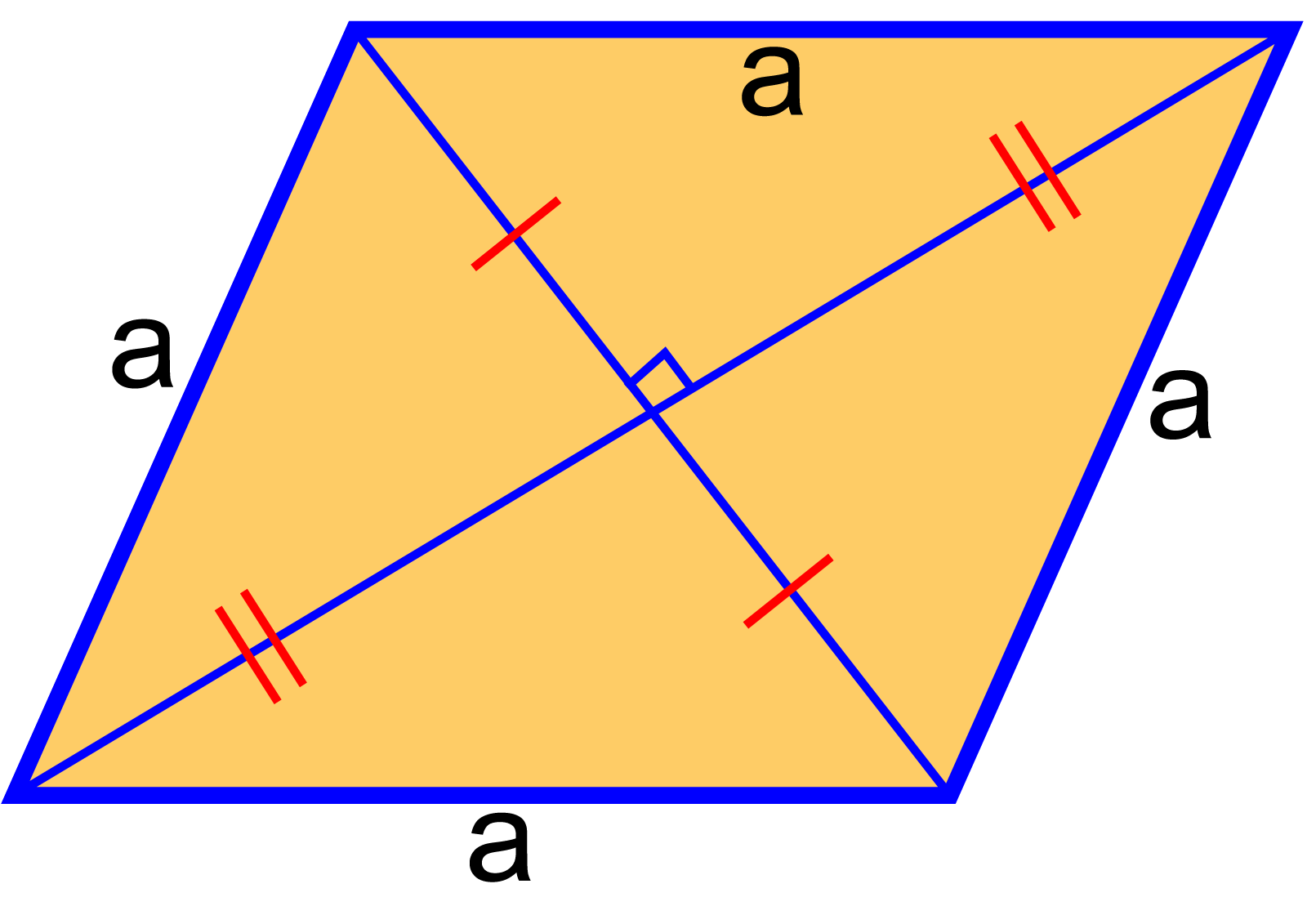
প্রকৃতপক্ষে, রম্বস হলো সামান্তরিকের একটি বিশেষ রূপ অর্থাৎ, সামান্তরিকের সন্নিহিত বাহুদ্বয় সমান হলে তখন তা রম্বস হয়ে যায়।
রম্বসকে অনেকসময় ডায়মন্ড বলা হয় কারণ এটি দেখতে অনেকটা ডায়মন্ডের মত।
আবার এটিকে সমবাহু চতুর্ভুজও বলা হয় কারণ এর চারটি বাহুর দৈর্ঘ্য পরস্পর সমান।
রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
রম্বসের বিপরীত কোণগুলো পরস্পর সমান।
রম্বস উদাহরণ

রম্বসের সূত্র
- রম্বসের পরিসীমার সূত্র
- রম্বসের কর্ণ নির্ণয়ের সূত্র
- রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র
- রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র
রম্বসের পরিসীমা
রম্বসের বাহুগুলোর সমষ্টিকে রম্বসের পরিসীমা বলে।
যেহেতু রম্বসের বাহুগুলো পরস্পর সমান, তাই রম্বসের একটি বাহু জানা থাকলে এর পরিসীমা নির্ণয় করা যায়। আবার রম্বসের কর্ণ দুইটি জানা থাকলে সেখান থেকে এর বাহুর দৈর্ঘ্য নির্ণয় করা যায়; অতপর রম্বসের পরিসীমা নির্ণয় করা যায়।
রম্বসের পরিসীমার সূত্র
মনে করি, ABCD একটি রম্বস এবং AB = BC = CD = AD = a.
আমরা জানি, রম্বসের বাহুগুলো পরস্পর সমান।
সুতরাং, রম্বসের পরিসীমা P হলে,
P = (AB + BC + CD + AD) একক
বা, P = (a + a + a + a) একক
∴ P = 4a একক

ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a হলে, পরিসীমা
P = 4a একক
রম্বসের কর্ণ
রম্বসের বিপরীত কৌণিক বিন্দু দুইটি যোগ করলে যে রেখাংশ পাওয়া যায় তাকে রম্বসের কর্ণ বলে।
রম্বসের এরূপ দুই জোড়া বিপরীত কৌণিক বিন্দু রয়েছে। দুই জোড়া কৌণিক বিন্দুর জন্য দুইট কর্ণ পাওয়া যায়। তাই রম্বসের কর্ণ দুইটি।
রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমুদ্বখণ্ডিত করে।
রম্বসের কর্ণ নির্ণয়ের সূত্র
রম্বসের বাহুর দৈর্ঘ্য জানা থাকলে রম্বসের কর্ণের দৈর্ঘ্য নির্ণয় করা যায়। তাহলে দেখা যাক- কিভাবে রম্বসের কর্ণ নির্ণয়ের সূত্র উদ্ভাবন করা যায়।
মনে করি, ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য AB, BC, CD ও AD; এবং AC ও BD এর দুইটি কর্ণ।
যেহেতু রম্বসের বাহুগুলো পরস্পর সমান, তাহলে মনে করি, AB = BC = CD = AD = a এবং কর্ণ AC = d1 ও BD = d2
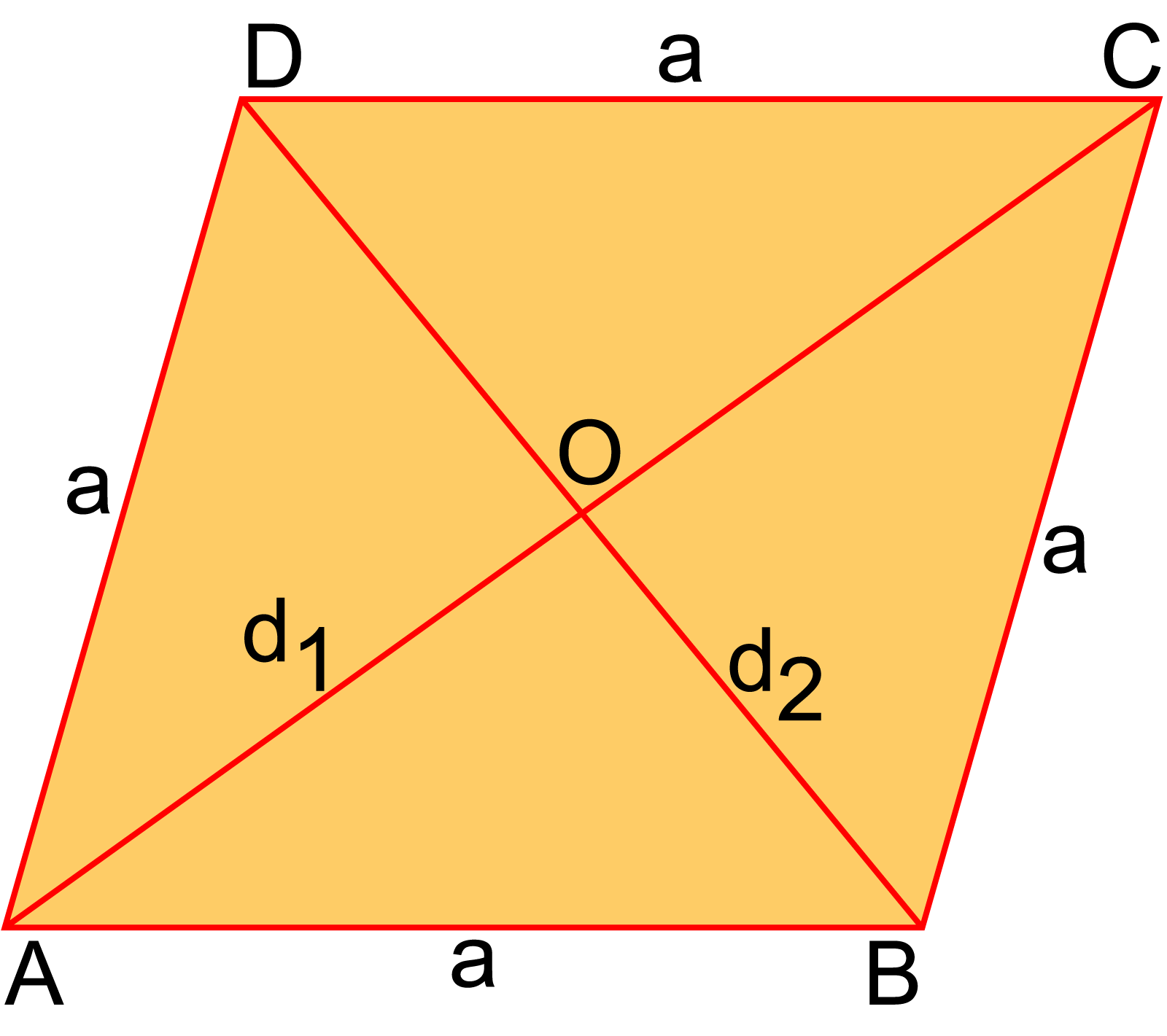
△ABC -এ কোসাইন ল (law of cosines) হতে পাই,
AC2 = AB2 + BC2 - 2AB.BC.cosB
বা, d12 = a2 + a2 - 2a.a cosB
বা, d1 = √2a2 - 2a2 cosB
বা, d1 = √2a2 - 2a2 cos(180°-A) [∵ A + B = 180°]
বা, d1 = √2a2 - 2a2 (-cosA)
বা, d1 = √2a2 + 2a2 cosA
বা, d1 = √a2(2 + 2cosA)
∴ d1 = a√2 + 2cosA
আবার, △ABD -এ কোসাইন ল (law of cosines) হতে পাই,
BD2 = AB2 + AD2 - 2AB.AD.cosA
বা, BD = √AB2 + AD2 - 2AB.AD.cosA
বা, d2 = √AB2 + AD2 - 2a.a cosA
বা, d2 = √a2 + a2 - 2a2cosA
বা, d2 = √2a2 - 2a2cosA
বা, d2 = √a2(2 - 2cosA)
বা, d2 = a√2 - 2cosA
ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a এবং বৃহত্তর ও ক্ষুত্রতর কর্ণ যথাক্রমে d1 ও d2 হলে,
d1 = a√2 + 2cosA
d2 = a√2 - 2cosA
রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র
রম্বসের কর্ণদ্বয় জানা থাকলে অথবা রম্বসের ক্ষেত্রফল ও একটি কর্ণ দেওয়া থাকলে রম্বসের বাহুর দৈর্ঘ্য নির্ণয় করা যায়। তাহলে দেখা যাক, রম্বসের কর্ণ দুইট দেওয়া থাকলে কিভাবে রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র উদ্ভাবন করা যায়।
প্রথম পদ্ধতিঃ মনে করি, ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a এবং কর্ণ দুইটি d1 ও d2 পরস্পর o বিন্দেুতে ছেদ করেছে। জানা আছে, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
∴ OA = d12 এবং OB = d22
∴ OA2 = d124 এবং OB2 = d224
আবার, ∠AOB = ৯০°
∴ সমকোণী △AOB থেকে পিথাগোরাসের উপপাদ্য অনুসারে লিখা যায়,
AB2 = OA2 + OB2
বা, a2 = d124 + d224
বা, a2 = d12 + d224
বা, a = √d12 + d22√4
∴ a = √d12 + d222
দ্বিতীয় পদ্ধতিঃ জানা আছে সামান্তরিকের বাহুগুলোর উপর অঙ্কিত বর্গক্ষেত্রগুলোর সমষ্টি ঐ সামান্তরিকের কর্ণ দুইটির উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান। রম্বস একটি সামান্তরিক।
∴ AB2 + BC2 + CD2 + AD2 = d12 + d22
বা, a2 + a2 + a2 + a2 = d12 + d22
বা, 4a2 = d12 + d22
বা, a = √d12 + d22√4
∴ a = √d12 + d222
ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a এবং কর্ণ দুইটি d1 ও d2 হলে,
a = √d12 + d222
রম্বসের ক্ষেত্রফল নির্ণয়
রম্বসের ক্ষেত্রফল বলতে বুঝায়, এর চারটি বাহু দ্বারা বেষ্টিত জায়গা। রম্বসের কর্ণদ্বয়ের মান জানা থাকলে এর ক্ষেত্রফল নির্ণয় করা যায়।
আবার, রম্বসের একটি বাহু ও সন্নিহিত কোণের পরিমাপ দেওয়া থাকলে এর কর্ণ নির্ণয় করা যায়; অতপর কর্ণদ্বয়ের মান ব্যবহার করে রম্বসের ক্ষেত্রফল নির্ণয় করা যায়। রম্বসের ক্ষেত্রফল একাধিক পদ্ধতিতে নির্ণয় করা যায়।
রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র
প্রথম পদ্ধতিঃ রম্বসের কর্ণদ্বয়ের গুণফলকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়।
ABCD রম্বসের কর্ণ দুইটি d1 ও d2 হলে, এর ক্ষেত্রফল হবে
A = 12 d1d2 বর্গ একক
ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a, কর্ণ যথাক্রমে d1 ও d2 এবং ক্ষেত্রফল A হলে,
A = 12 d1d2 বর্গ একক
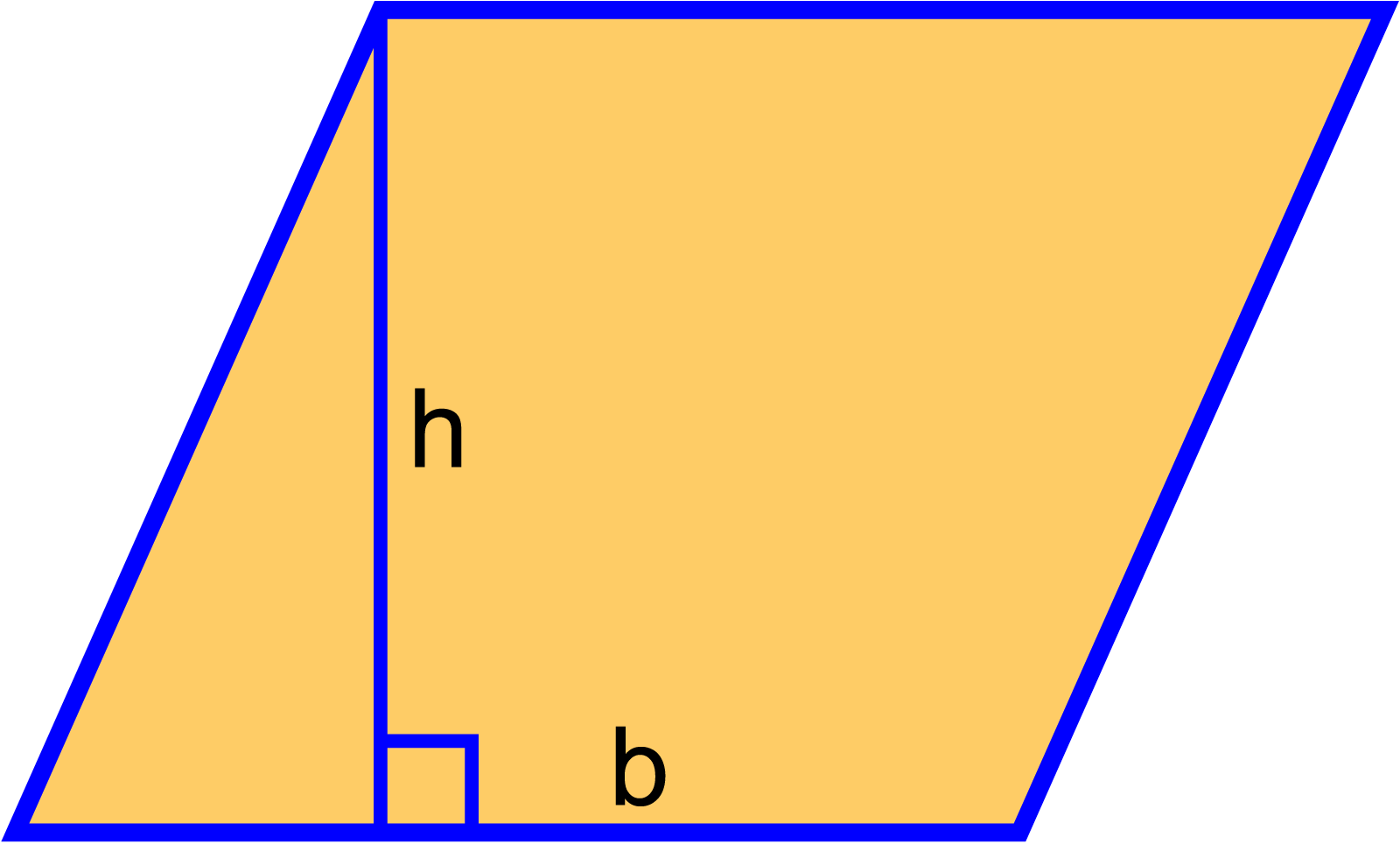
দ্বিতীয় পদ্ধতিঃ সামান্তরিকের ভূমিকে উচ্চতা দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়। রম্বস একটি সামান্তরিক।
রম্বসের ভূমিকে উচ্চতা দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়।
মনে করি, ABCD রম্বসের বাহু বা ভূমি a, উচ্চতা h এবং ক্ষেত্রফল A হলে,
A = a.h বর্গ একক
ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a, উচ্চতা h এবং ক্ষেত্রফল A হলে,
A = ah বর্গ একক
তৃতীয় পদ্ধতিঃ রম্বসের যেকোন কোণের সাইন(sine)কে বাহুর বর্গ দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়।
মনে করি, ABCD রম্বসের বাহু a এবং ক্ষেত্রফল A হলে,
A = a2sinA বর্গ একক
চতুর্থ পদ্ধতিঃ মনে করি, ABCD রম্বসের বাহুর দৈর্ঘ্য a এবং BD একটি কর্ণ।
□ABCD = △ABD + △BCD
বা, □ABCD = △ABD + △ABD [∵ △ABD ≅ △BCD]
বা, □ABCD = 2△ABD
বা, □ABCD = 2. 12 a. a sinA
∴ □ABCD = a2sinA
ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a, সন্নিহিত ∠A হলে,
রম্বসের ক্ষেত্রফল = a2sinA বর্গ একক