বৃত্তের বৈশিষ্ট্য

বৃত্তের সংজ্ঞা বিশ্লেষণ করলে বৃত্ত সংক্রান্ত কতকগুলো মৌলিক উপাদান ও বৃত্তের বৈশিষ্ট্য পরিলক্ষিত হয়। আবার বৃত্তের বিভিন্ন অংশ যেমন বৃত্তের কেন্দ্র, বৃত্তের ব্যাসার্ধ, বৃত্তের ব্যাস, বৃত্তের পরিধি, বৃত্তের ক্ষেত্রফল, বৃত্তের স্পর্শক, বৃত্তের প্রতিসমতা ইত্যাদি বিশ্লেষণ করলে বৃত্তের বৈশিষ্ট্য গুলো কি কি তা স্পষ্ট হয়ে ওঠে।

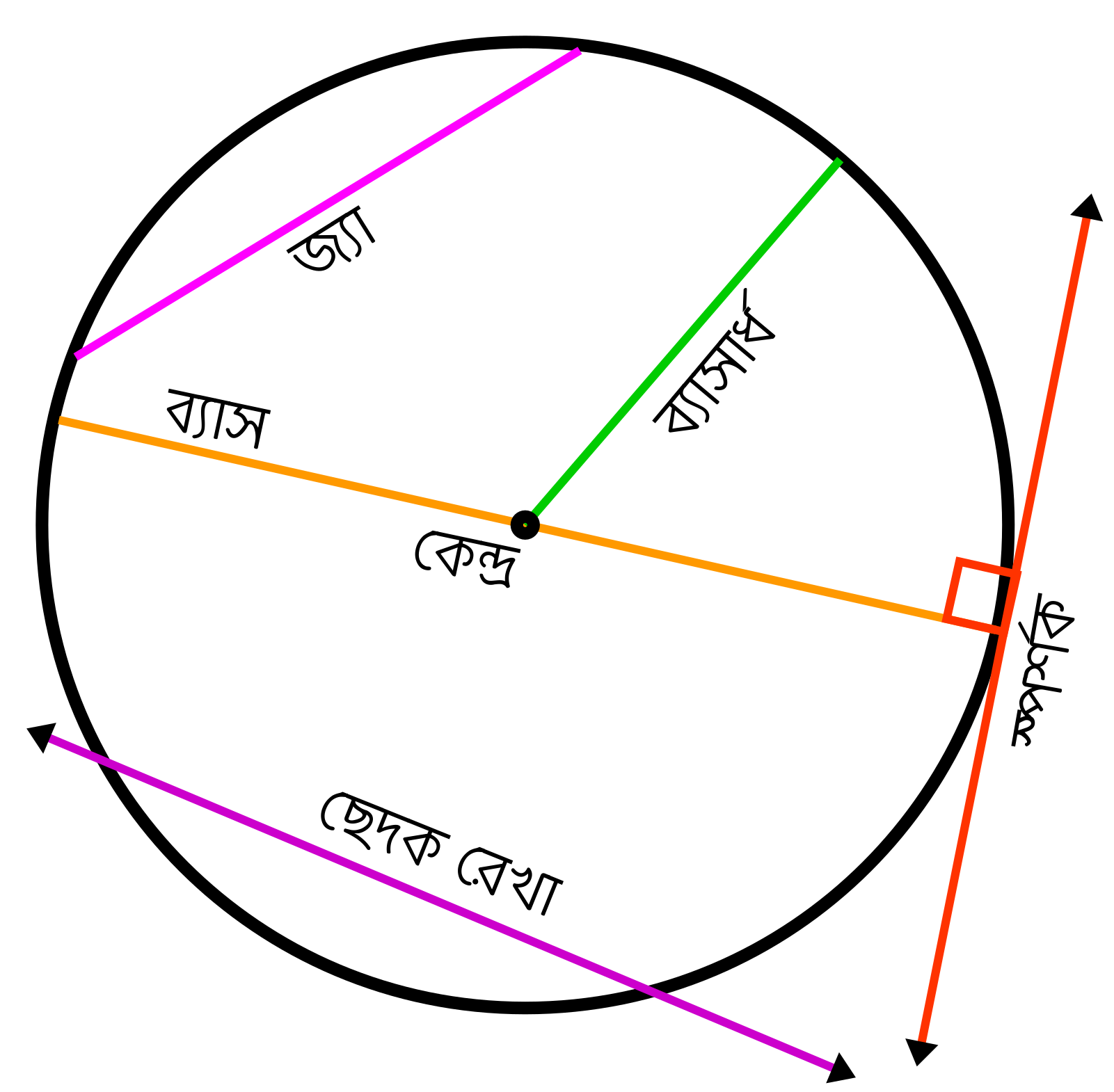
বৃত্ত বিশ্লেষণ করলে যেসব বৃত্তের বৈশিষ্ট্য পরিলক্ষিত হয়, বৃত্ত চিত্র সহ তার একটি তালিকা নিচে উল্লেখ করা হলোঃ

• একটি নির্দিষ্ট দৈর্ঘ্যকে পরিসীমা বিবেচনা করে যেসব দ্বিমাত্রিক ক্ষেত্র যেমন ত্রিভুজ, চতুর্ভুজ, বহুভুজ, বৃত্ত ইত্যাদি অঙ্কন করা যায় তাদের মধ্যে বৃত্ত ক্ষেত্রটির ক্ষেত্রফল হবে সবচেয়ে বেশি।
• বৃত্তের পরিধি ও বৃত্তের ব্যাসার্ধ সমানুপাতিক।
• বৃত্তের একই চাপের উপর দণ্ডায়মান বৃত্তস্থ কোণগুলো পরস্পর সমান।
• বৃত্তের পরিধি ও ব্যাসের অনুপাত সবসময়ই ২২ : ৭, যা π বলে পরিচিত অর্থাৎ, π = ২২৭।
• বৃত্তের কেন্দ্র থেকে ব্যাসভিন্ন যেকোনো জ্যা এর উপর অঙ্কিত লম্ব ঐ জ্যা কে সমদ্বিখণ্ডিত করে।
• বৃত্তের দুইটি সমান সমান জ্যা পরস্পরকে ছেদ করলে তাদের একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান।
• একটি বৃত্তের অসংখ্য ব্যাসার্ধ আঁকা যায়।
• একই সমতলে অবস্থিত এবং সমরেখ নয় এমন তিনটি বিন্দু দিয়ে একটি ও কেবল একটি বৃত্ত অঙ্কন করা যায়।
• বৃত্তের সমান সমান জ্যা এর মধ্যবিন্দুগুলো সমবৃত্ত।
• বৃত্তস্থ ট্রাপিজিয়ামের তির্যক বাহুদ্বয় পরস্পর সমান।
• দুইটি সমান্তরাল জ্যা এর মধ্যবিন্দুর সংযোজক সরলরেখা কেন্দ্রগামী এবং জ্যা দুইটির উপর লম্ব।
• বৃত্তের যেকোনো জ্যা এর লম্বদ্বিখণ্ডক কেন্দ্রগামী।
• বৃত্তে অন্তর্লিখিত চতুর্ভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় তা বিপরীত অন্তঃস্থ কোণের সমান।
• বৃত্তস্থ চতুর্ভুজের যেকোনো কোণের সমদ্বিখণ্ডক ও তার বিপরীত কোণের বহির্দ্বিখণ্ডক বৃত্তের উপর ছেদ করে।
• বৃত্তের একই চাপের উপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ।
• সব বৃত্তই পরস্পর সদৃশ।
• যেসব বৃত্তের ব্যাসার্ধ পরস্পর সমান, সেসব বৃত্ত পরস্পর সর্বসম।
• বৃত্তের ক্ষেত্রফল ও তার ব্যাসার্ধের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল সমানুপাতিক।
• বৃত্তের অধিচাপে অন্তর্লিখিত কোণ একটি সূক্ষ্মকোণ।
• যে বৃত্তের কেন্দ্র মূলবিন্দু (0,0) এবং ব্যাসার্ধ ১ একক, তার নাম একক বৃত্ত (unit circle)।
• বৃত্তের ব্যাস বৃত্তের ব্যাসার্ধের দ্বিগুণ।
• বৃত্তের প্রত্যেক ছেদকের ছেদবিন্দুদ্বয়ের অন্তর্বর্তী সকল বিন্দু বৃত্তের অভ্যন্তরে থাকে।
• যেকোনো বৃত্তের স্পর্শবিন্দুতে স্পর্শকের উপর অঙ্কিত লম্ব কেন্দ্রগামী।

• বৃত্তে অন্তর্লিখিত কোনো চতুর্ভুজের কর্ণ দুইটি পরস্পর লম্ব হলে, তাদের ছেদ বিন্দু হতে কোনো বাহুর উপর অঙ্কিত লম্ব বিপরীত বাহুকে সমদ্বিখণ্ডিত করে।
• বৃত্তের ঘূর্ণন প্রতিসমতার মাত্রা অসীম।
• ত্রিভুজের লম্ববিন্দু ও পরিকেন্দ্রের সংযোজক রেখাংশের মধ্যবিন্দুই নববিন্দুবৃত্তের কেন্দ্র।
• বৃত্তের কোনো বিন্দু দিয়ে অঙ্কিত ব্যাসার্ধ এবং ঐ বিন্দুতে ব্যাসার্ধের উপর অঙ্কিত লম্ব উক্ত বিন্দুতে বৃত্তটির স্পর্শক হয়।
• বৃত্তের ব্যাস ভিন্ন যেকোনো জ্যা এর মধ্যবিন্দু ও কেন্দ্রের সংযোজক সরলরেখা ঐ জ্যা এর উপর লম্ব।
• কোন বৃত্তের উপচাপে অন্তর্লিখিত কোণ একটি স্থুলকোণ।
• দুইটি বৃত্ত পরস্পরকে অন্তঃস্পর্শ করলে, এদের কেন্দ্রদ্বয় ও স্পর্শ বিন্দু সমরেখ।
• বৃত্তের প্রমিত সমীকরণ হলো (x-a)² + (y-b)² = c² যেখানে বৃত্তের কেন্দ্র (a,b) এবং ব্যাসার্ধ c একক।
• দুইটি বৃত্ত পরস্পর বহিঃস্পর্শ করলে, স্পর্শ বিন্দু ছাড়া প্রত্যেক বৃত্তের অন্য সব বিন্দু অপর বৃত্তের বাইরে থাকে।
• অর্ধবৃত্তস্থ কোণ সবসময়ই এক সমকোণ বা ৯০°।
• বৃত্তের ক্ষেত্রফল ও বৃত্তে অন্তর্লিখিত বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত π : 2.
• বৃত্তের সমান সমান জ্যা কেন্দ্র হতে সমদূরবর্তী।
• বৃত্তের ব্যাসার্ধ r একক হলে বৃত্তের ক্ষেত্রফল = πr² বর্গ একক।
• বৃত্তে অন্তর্লিখিত চতুর্ভুজের বিপরীত কোণ দুইটি পরস্পর সম্পূরক।
• একটি বৃত্তের ব্যাসের দুই প্রান্ত থেকে তার বিপরীত দিকে দুইটি সমান জ্যা অঙ্কন করলে অঙ্কিত জ্যাদ্বয় পরস্পর সমান্তরাল হয়।
• বৃত্তের ব্যাসই বৃহত্তম জ্যা।
• বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে বৃত্তে দুইটি স্পর্শক আঁকলে ঐ বিন্দু থেকে স্পর্শ বিন্দুদ্বয়ের দুরত্ব সমান হয়।
• দুইটি বৃত্ত পরস্পর অন্তঃস্পর্শ করলে, স্পর্শ বিন্দু ছাড়া ছোট বৃত্তের অন্য সব বিন্দু বড় বৃত্তটির অভ্যন্তরে থাকে।
• কোনো চতুর্ভুজের দুইটি বিপরীত কোণের সমষ্টি ১৮০° হলে, বিন্দু চারটি সমবৃত্ত বা একই বৃত্তের উপর অবস্থিত হয়।
• যেকোনো সরলরেখা একটি বৃত্তকে সর্বোচ্চ দুইটি বিন্দুতে ছেদ করতে পারে।
• একটি বৃত্ত যদি একটি সমকোণী ত্রিভুজের তিনটি শীর্ষবিন্দু দিয়ে অতিক্রম করে তাহলে বৃত্তটির কেন্দ্র হবে অতিভুজের মধ্যবিন্দু।
• বৃত্তের ব্যাসার্ধ r একক হলে বৃত্তের পরিধি =2πr একক।

• দুইটি বৃত্ত পরস্পর বহিঃস্পর্শ করলে, এদের কেন্দ্রদ্বয় ও স্পর্শ বিন্দু সমরেখ অর্থাৎ একই রেখায় অবস্থিত।
• একটি বৃত্তের দুইটি জ্যা পরস্পরকে সমদ্বিখণ্ডিত করলে তাদের ছেদবিন্দুটি বৃত্তের কেন্দ্র হয়।
• বৃত্তের কেন্দ্রগামী যেকোনো রেখাই এর প্রতিসাম্য রেখা।
• বৃত্তের কোনো বিন্দু থেকে বৃত্তে দুইটি স্পর্শক টানলে ঐ বিন্দু ও কেন্দ্রের সংযোজক সরলরেখা স্পর্শ-জ্যা এর উপর লম্ব।
• বৃত্তের যেসব জ্যা কেন্দ্র হতে সমদূরবর্তী সেইসব জ্যা পরস্পর সমান।
• একটি নির্দিষ্ট কেন্দ্রবিশিষ্ট অংসখ্য বৃত্ত আঁকা যায়।
• বৃত্তের কেন্দ্র মূলবিন্দু (0,0) এবং ব্যাসার্ধ a একক, তার সমীকরণটি হবে x²+y² = a².
• দুইটি বৃত্ত পরস্পরকে অন্তঃস্পর্শ করলে, কেন্দ্রদ্বয়ের দূরত্ব বৃত্তদ্বয়ের ব্যাসার্ধের অন্তরের সমান।
• সব সর্বসম বৃত্ত সদৃশ কিন্তু সব সদৃশ বৃত্ত সর্বসম নয়।
• বৃত্তের দুইটি জ্যা এর মধ্যে বৃহত্তর জ্যাটি ক্ষুদ্রতর জ্যা অপেক্ষা কেন্দ্রের নিকটতর।
• দুইটি বিন্দুর সংযোজক রেখাংশ তার একই পাশে অবস্থিত অপর দুইটি বিন্দুতে সমান সমান কোণ উৎপন্ন করলে, বিন্দু চারটি সমবৃত্ত হয়।
• সমকোণী ত্রিভুজের অতিভুজকে ব্যাস বিবেচনা করে বৃত্ত অঙ্কন করলে তা সমকৌণিক শীর্ষবিন্দু দিয়ে অতিক্রম করে।
• বৃত্তে অন্তর্লিখিত সামান্তরিক একটি আয়তক্ষেত্র।
• সমান সমান ভূমির উপর অবস্থিত যেকোনো দুইটি ত্রিভুজের শিরঃকোণদ্বয় সম্পূরক হলে, তাদের পরিবৃত্তদ্বয় সমান হয়।
• বৃত্তের যেকোনো বিন্দুতে অঙ্কিত স্পর্শক স্পশবিন্দুগামী ব্যাসার্ধের উপর লম্ব।
• সমান ক্ষেত্রফলবিশিষ্ট যেসব বহুভুজ যেমন ত্রিভুজ, চতুর্ভুজ, পঞ্চভুজ বা বৃত্ত আঁকা যায়, সেইসব বহুভুজের পরিসীমাগুলোর মধ্যে বৃত্তের পরিধি সবচেয়ে কম।
• বৃত্তের প্রতিসাম্য রেখা অসীম।
• বৃত্তের কোনো বিন্দুতে একটি ও কেবল একটি স্পর্শক অঙ্কন করা যায়।
• দুইটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করলে, কেন্দ্রদ্বয়ের দূরত্ব বৃত্তদ্বয়ের ব্যাসার্ধের সমষ্টির সমান।
• নববিন্দুবৃত্তের ব্যাসার্ধ ত্রিভুজের পরিব্যাসার্ধের অর্ধেকের সমান।
• বৃত্তে অন্তর্লিখিত কোনো চতুর্ভুজের কর্ণদ্বয়ের অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফল ঐ চতুর্ভুজের বিপরীত বাহুদ্বয়ের অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান।

বৃত্তের বৈশিষ্ট্য সংক্রান্ত যেসব প্রশ্নসমূহ সচরাচর মানুষ করে থাকে।

উত্তরঃ বৃত্তের বৈশিষ্ট্য পঞ্চম শ্রেণী উপযোগী কতকগুলো বৈশিষ্ট্য নিম্নরূপ:

1. একটি বৃত্তের ব্যাসের দৈর্ঘ্য তার ব্যাসার্ধের দৈর্ঘ্যের দ্বিগুণ।
2. একটি বৃত্তের অসংখ্য ব্যাস আঁকা যায় কিন্তু সকল ব্যাসের দৈর্ঘ্য পরস্পর সমান।
3. একটি বৃত্তের কেবল একটি মাত্র কেন্দ্র থাকে।
4. একটি বৃত্তের উপর অসংখ্য বিন্দু থাকে।
5. একটি বৃত্তে অসংখ্য জ্যা আঁকা যায়।

উত্তরঃ একটি বৃত্তের ৩ টি বৈশিষ্ট্য নিচে উল্লেখ করা হলো:

1. একটি বৃত্তের অসংখ্য ব্যাসার্ধ আঁকা যায় কিন্তু সকল ব্যাসার্ধের দৈর্ঘ্য পরস্পর সমান।
2. বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে বৃত্তে সর্বোচ্চ দুইটি স্পর্শক আঁকা যায়।
3. একটি কেন্দ্র দিয়ে অসংখ্য বৃত্ত আঁকা যায়।

উত্তরঃ একটি বৃত্তের সংজ্ঞা ও চিত্র বিশ্লেষণ করলে যেসব বৈশিষ্ট্য পাওয়া যায় তা থেকে কয়েকটি বৃত্তের বৈশিষ্ট্য উল্লেখ করা হলো:

1. বৃত্তের কেন্দ্র থেকে তার পরিধির উপর যেকোনো দূরত্ব পরস্পর সমান।
2. বৃত্তের পরিধির উপর যেকোনো একটি বিন্দুতে কেবল একটি স্পর্শক আঁকা সম্ভব।
3. বৃত্তের যেকোনো জ্যা এর লম্ব সমদ্বিখণ্ডক কেন্দ্র দিয়ে যায়।