বিপ্রতীপ কোণ কাকে বলে

বিপ্রতীপ কোণ

দুইটি সরলরেখা পরস্পর ছেদ করলে ছেদ বিন্দুতে যে চারটি কোণ উৎপন্ন হয়, তাদের যেকোনো একটিকে তার বিপরীত কোণের বিপ্রতীপ কোণ বলে। আরেকটু পরিশীলিত আকারে সংজ্ঞায়িত করলে দাঁড়ায়,

একটি কোণের বিপরীত রশ্মিদ্বয় ঐ কোণের বিপরীত দিকে একই শীর্ষবিন্দুতে যে কোণ উৎপন্ন করে তাকে পূর্বের কোণের বিপ্রতীপ কোণ বলে।

অন্যভাবে বলা যায়, দুইটি সরলরেখা কোনো একটি বিন্দুতে পরস্পর ছেদ করলে, ছেদ বিন্দুতে যে দুই জোড়া বিপরীত কোণ উৎপন্ন হয়, প্রতিজোড়া বিপরীত কোণের একটিকে বিপ্রতীপ কোণ কোণ বলে।

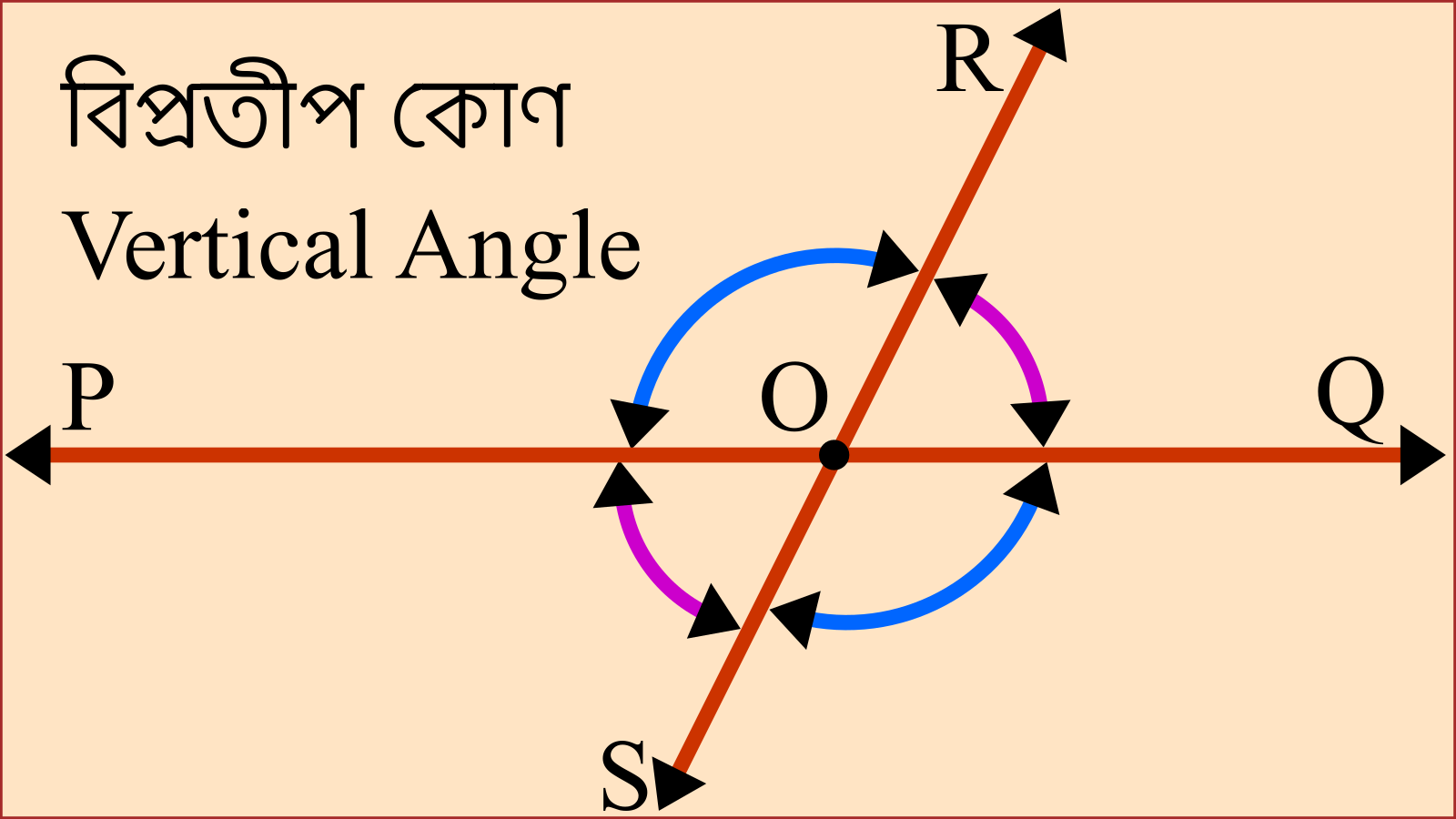
বিপ্রতীপ কোণগুলোর শীর্ষবিন্দু সাধারণ হয় অর্থাৎ, সবগুলো বিপ্রতীপ কোণ একই শীর্ষ বিন্দু থেকে উৎপন্ন হয়। বিপ্রতীপ কোণদ্বয় পরস্পর সমান হয়।

চিত্রে, PQ এবং RS রেখা দুইটি পরস্পর O বিন্দুতে মিলিত হয়েছে। ফলে O বিন্দুতে ∠POR, ∠POS, ∠SOQ এবং ∠QOR চারটি কোণ উৎপন্ন হয়েছে। আবার, ∠POR কোণের বাহু দুইটির বিপরীত রশ্মি OQ এবং OS দ্বারা ∠SOQ উৎপন্ন হয়েছে। সুতরাং, ∠POR এর বিপ্রতীপ ∠SOQ.

তদ্রূপ, ∠POS কোণের বাহু দুইটির বিপরীত রশ্মি OQ এবং OR দ্বারা ∠QOR উৎপন্ন হয়েছে। সুতরাং, ∠POS এর বিপ্রতীপ ∠QOR.

আবার, যেহেতু বিপ্রতীপ কোণগুলো পরস্পর সমান, সেকারণে,

সুতরাং, ∠POR = ∠SOQ এবং ∠POS = ∠QOR.

বিপ্রতীপ কোণের চিত্র বিশ্লেষণ

বিপ্রতীপ কোণের চিত্র বিশ্লেষণ বলতে বিপ্রতীপ কোণ কিভাবে উৎপন্ন হয়, কোণগুলোর শীর্ষবিন্দুতে সর্বমোট কয়টি কোণ উৎপন্ন হয়, উৎপন্ন বিপ্রতীপ কোণগুলোর মধ্যে পারস্পারিক সম্পর্ক, বিপ্রতীপ কোণদ্বয় কেন বা কি কারণে সমান হয় ইত্যাদিকে বুঝায়।

চিত্রে, AB ও CD সরলরেখা দুইটি পরস্পর O বিন্দুতে ছেদ করেছে। ফলে O বিন্দুতে চারটি কোণ ∠AOD, ∠AOC, ∠COB, এবং ∠BOD উৎপন্ন হয়েছে।

আবার, ∠AOD কোণের বাহু দুইটি OA এবং OD এর বিপরীত রশ্মিদ্বয় যথাক্রমে OB এবং OC দ্বারা ∠COB উৎপন্ন হয়েছে। একারণে, ∠AOD এর বিপ্রতীপ ∠COB.

একইভাবে, ∠AOC কোণের বাহু দুইটি OA এবং OC এর বিপরীত রশ্মিদ্বয় যথাক্রমে OB ও OD দ্বারা ∠BOD উৎপন্ন হয়েছে। সেইজন্য, ∠AOC এর বিপ্রতীপ ∠BOD.

এখন, বিপ্রতীপ কোণদ্বয় সমান কেন হয় - এই প্রশ্নের খুঁজে বের করা যাক।

∠AOC এর সম্পূরক কোণ ∠AOD. আবার, একই কোণ ∠AOC এর সম্পূরক কোণ ∠COB.

তাহলে, একই কোণের সম্পূরক কোণ দুইটি পরস্পর সমান। সুতরাং, ∠AOD = ∠COB.

∴ ∠AOD = বিপ্রতীপ ∠COB.

সুতরাং, বিপ্রতীপ কোণগুলো পরস্পর সমান।

সুতরাং, ∠AOD = বিপ্রতীপ ∠COB এবং ∠AOC = বিপ্রতীপ ∠BOD.

বিপ্রতীপ কোণ বিষয়ক সৃজনশীল প্রশ্ন

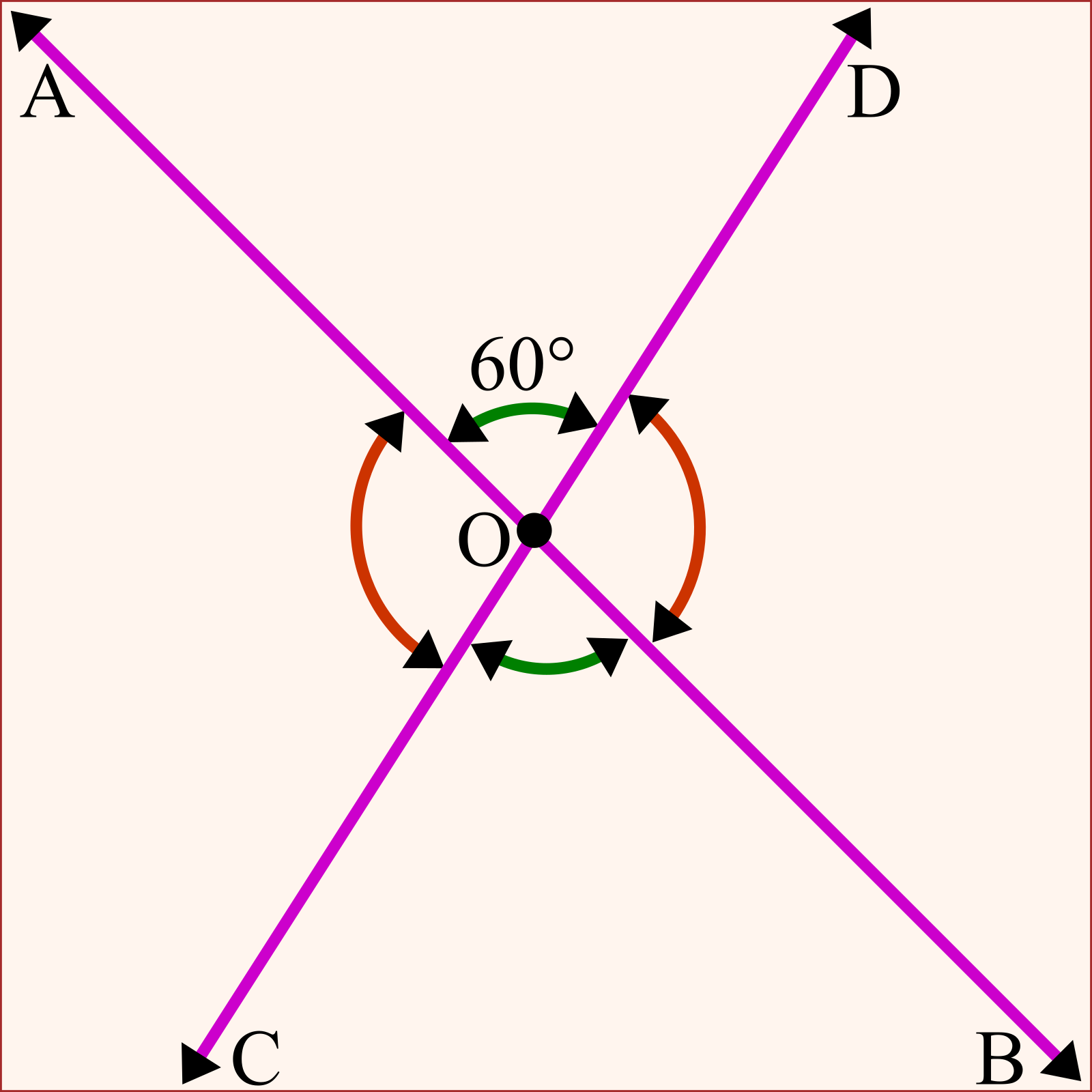
প্রশ্ন: AB ও CD সরলরেখা দুইটি পরস্পর O বিন্দুতে মিলিত হয়ে ∠AOD = ৬০° কোণ উৎপন্ন করেছে।

ক. ∠AOD এর বিপ্রতীপ কোণ কত?
খ. অবশিষ্ট কোণগুলোর মান কত?
গ. উদ্দীপকের কোণের বিপ্রতীপ কোণদ্বয় নিয়ে একটি ত্রিভুজ গঠন করা হলে কোণ অনুসারে ত্রিভুজটি কোন ধরণের ত্রিভুজ হবে? উত্তরের স্বপক্ষে যুক্তিই বা কি?

উত্তর: ক. চিত্রে, AB ও CD সরলরেখাদ্বয় পরস্পর O বিন্দুতে ছেদ করে O বিন্দুতে চারটি কোণ ∠AOD, ∠AOC, ∠COB, এবং ∠BOD উৎপন্ন হয়েছে এবং ∠AOD = ৬০°।

এখন, ∠COB = বিপ্রতীপ ∠AOD
বা, ∠COB = ∠AOD
∴ ∠COB = ৬০° [∵ ∠AOD = ৬০°]

উত্তর: খ. ∠AOD এবং ∠AOC পরস্পর সম্পূরক কোণ।

∴ ∠AOD + ∠AOC = ১৮০°

বা, ৬০° + ∠AOC = ১৮০° [∵ ∠AOD = ৬০°]

বা, ∠AOC = ১৮০° - ৬০°

∴ ∠AOC = ১২০°।

আবার, ∠BOD = বিপ্রতীপ ∠AOC

বা, ∠BOD = ∠AOC

∴ ∠BOD = ১২০° [∵ ∠AOC = ১২০°]

সুতরাং, ∠AOD = ∠COB = ৬০°

এবং ∠AOC = ∠BOD = ১২০°

উত্তর: গ. উদ্দীপকে, ∠COB = বিপ্রতীপ ∠AOD

∴ ∠COB = ∠AOD = ৬০°

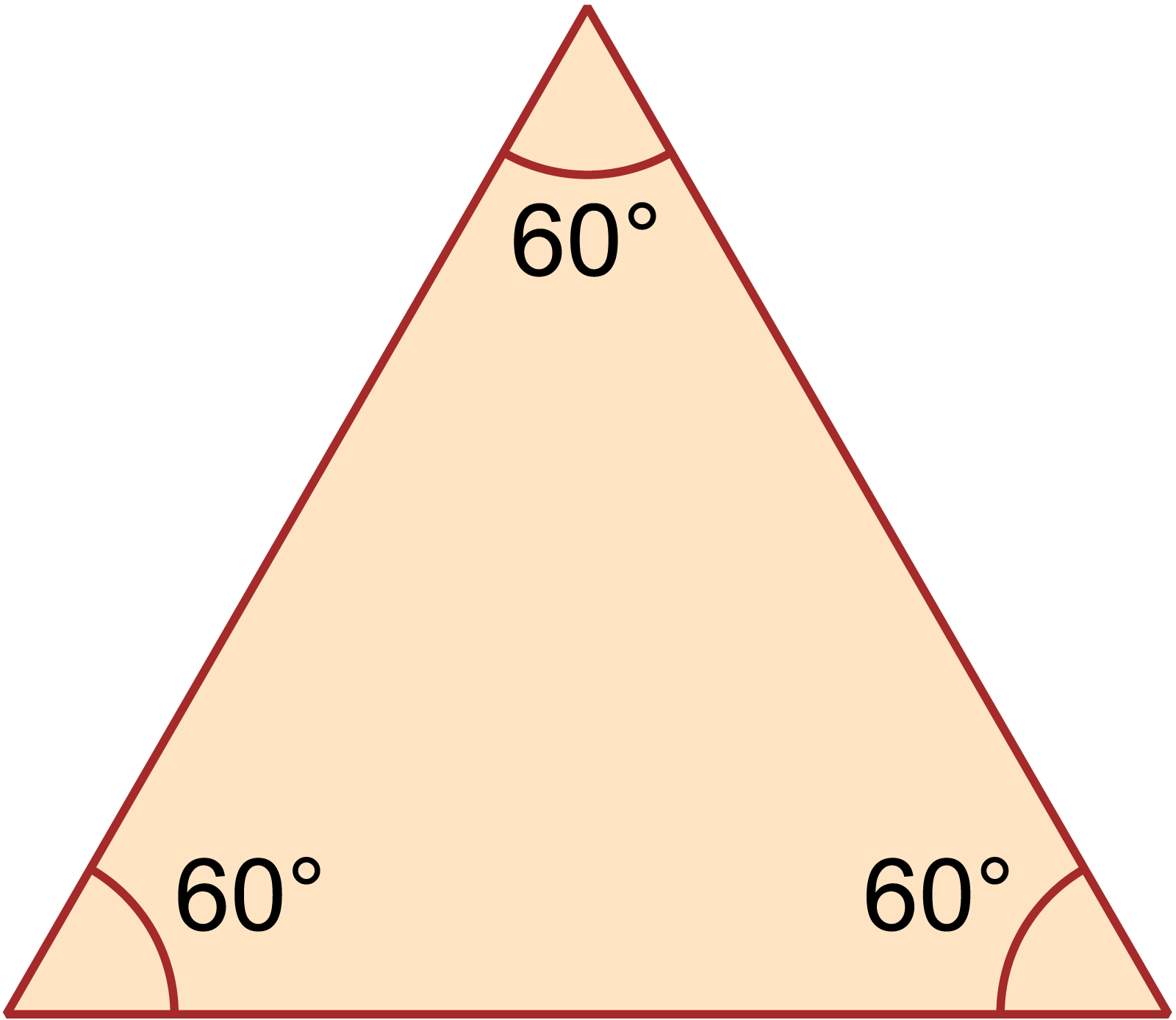
এখন, এই কোণ দুইটি দিয়ে একটি ত্রিভুজ গঠন করা হলো। এই ত্রিভুজের দুইটি কোণ ৬০°। ত্রিভুজটির দুইটি কোণ পরস্পর সমান বা ৬০°। এই কারণে, কোণ দুইটির বিপরীত বাহু দুইটিও পরস্পর সমান। তাই প্রাথমিকভাবে, ত্রিভুজটিকে একটি সমদ্বিবাহু ত্রিভুজ বলা যায়।

আবার, যেকোনো ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণ বা ১৮০°।

মনে করি, অবশিষ্ট কোণের মান x.

∴ x + ৬০° + ৬০° = ১৮০°

বা, x + ১২০° = ১৮০°

বা, x = ১৮০°- ১২০°

∴ x = ৬০°

অতএব, অবশিষ্ট কোণের পরিমাপও ৬০°।

সুতরাং, ত্রিভুজটির তিনটি কোণের প্রত্যেকটির পরিমাপ ৬০°।

ত্রিভুজটির তিনটি কোণ সমান বলে তাদের বিপরীত বাহুগুলোও পরস্পর সমান।

ত্রিভুজটি একটি সমবাহু ত্রিভুজ।