বিষমবাহু ত্রিভুজের বৈশিষ্ট্য

বিষমবাহু ত্রিভুজ বিশ্লেষণ করলে কতকগুলো বিষমবাহু ত্রিভুজের বৈশিষ্ট্য আমাদের চোখের সামনে ভেসে ওঠে। আর এসব বৈশিষ্ট্য সমূহ বিষমবাহু ত্রিভুজের সংজ্ঞা, প্রকৃতি ও গঠন প্রণালী, বাহুর দৈর্ঘ্য, কোণের পরিমাপ ইত্যাদি থেকে নিঃসৃত হয়। যেকোনো ধরণের ত্রিভুজ ও বিষমবাহু ত্রিভুজের বৈশিষ্ট্য সমূহের মধ্যে বেশকিছু বৈশিষ্ট্য সাধারণ থাকলেও এই ত্রিভুজের কতকগুলো মৌলিক বৈশিষ্ট্যও রয়েছে। এসব মৌলিক বৈশিষ্ট্য সমূহ বিষমবাহু ত্রিভুজকে অন্যান্য ত্রিভুজ থেকে পৃথক করেছে।

বিষমবাহু ত্রিভুজ অন্যান্য ত্রিভুজকে প্রতিনিধিত্ব করে বলেই বিষমবাহু ত্রিভুজের বৈশিষ্ট্য অন্যান্য ত্রিভুজের বৈশিষ্ট্যের সাথে সম্পর্কিত। একারণে বিষমবাহু ত্রিভুজের বৈশিষ্ট্য জানা থাকলে অন্যান্য সকল ত্রিভুজের বৈশিষ্ট্য জানা সহজ হয়ে যায়। গণিতের কিছু কিছু মৌলিক ধারণা বিষমবাহু ত্রিভুজের বৈশিষ্ট্যকে ভিত্তি করে গড়ে উঠেছে। তাছাড়া গণিতের বিভিন্ন শাখায় এই ত্রিভুজের বিভিন্ন বৈশিষ্ট্য নানাভাবে ব্যবহৃত হয়। মজার বিষয় হলো, বিষমবাহু ত্রিভুজের সাথে বৃত্ত সম্পর্কিত বৈশিষ্ট্য সমূহ পাঠ সত্যিই আনন্দদায়ক।

যাহোক, বিষমবাহু ত্রিভুজ সম্পর্কে পরিপূর্ণ জ্ঞান লাভ করতে হলে বিষমবাহু ত্রিভুজের বৈশিষ্ট্য সমূহ খুব ভালভাবে জানা জরুরী। এই ত্রিভুজের বেশকিছু বৈশিষ্ট্য সমূহ নিচে তুলে ধরা হলো।

1. বিষমবাহু ত্রিভুজের বাহু তিনটির দৈর্ঘ্য পরস্পর অসমান।
2. বিষমবাহু ত্রিভুজের মধ্যমাত্রয় পরস্পর অসমান।
3. বিষমবাহু ত্রিভুজের ভরকেন্দ্র থেকে বাহুত্রয়ের উপর অঙ্কিত লম্ব তিনটির দৈর্ঘ্য পরস্পর অসমান।
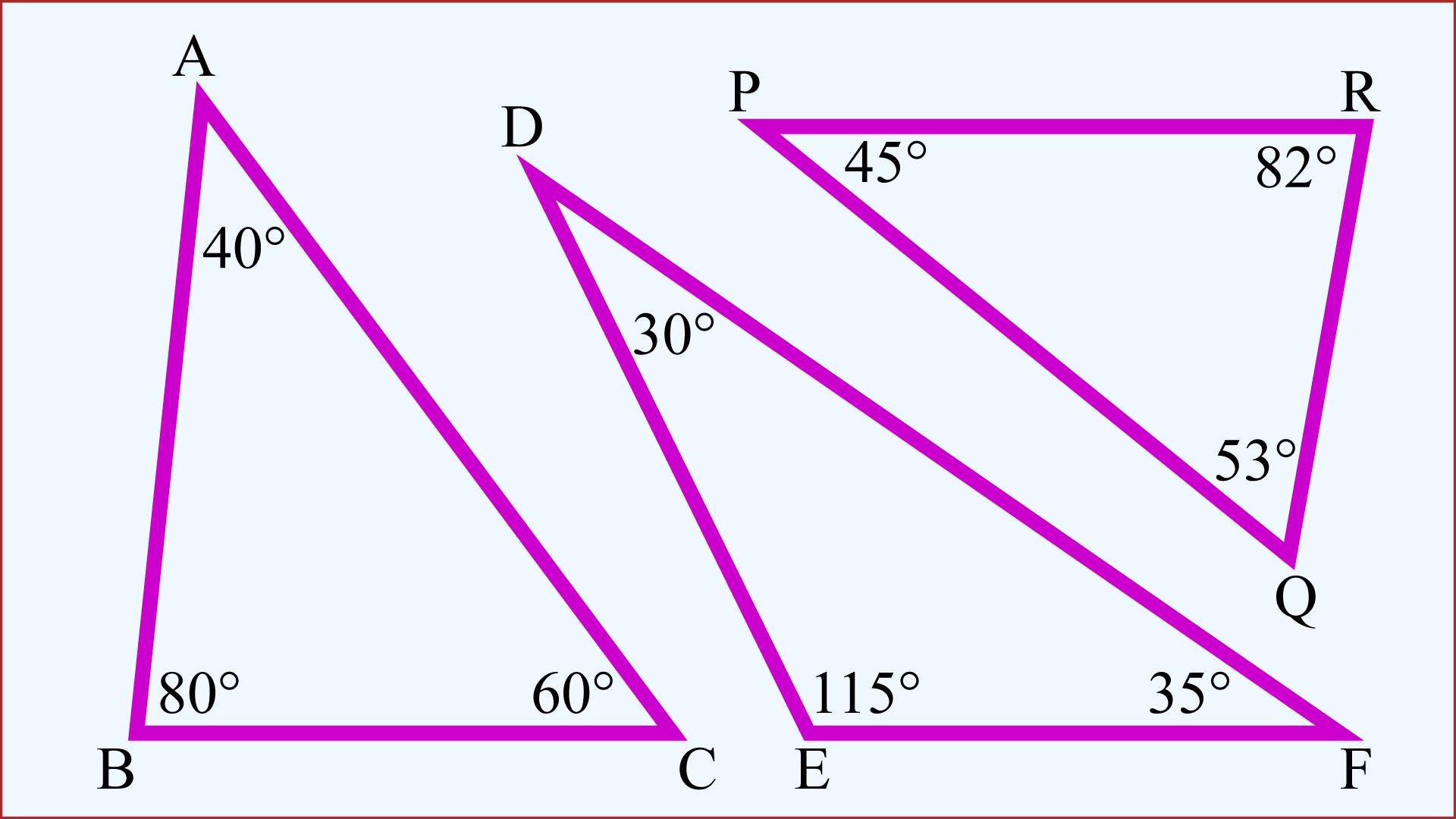
4. বিষমবাহু ত্রিভুজের কোণ তিনটির পরিমাপ পরস্পর অসমান।
5. বিষমবাহু ত্রিভুজের শীর্ষতিনটি থেকে বিপরীত বাহুগুলোর উপর অঙ্কিত লম্বত্রয় পরস্পর অসমান।
6. বিষমবাহু ত্রিভুজের শীর্ষত্রয় থেকে বিপরীত বাহুর উপর অঙ্কিত লম্ব তিনটি যে বিন্দুতে পরস্পর ছেদ করে তাকে লম্বকেন্দ্র (orthocenter) বলে।
7. বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য জানা থাকলে তার মধ্যমাগুলোর দৈর্ঘ্য নির্ণয় করা যায়।
8. স্থুলকোণী ত্রিভুজের স্থুলকোণ এর বিপরীত বাহুর উপর অঙ্কিত বর্গক্ষেত্র ঐ কোণের সন্নিহিত অন্য দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফল এবং ঐ দুই বাহুর যেকোনে একটি ও তার উপর অপর বাহুর লম্ব অভিক্ষেপের অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফলের দ্বিগুণের সমষ্টির সমান।
9. ত্রিভুজের যেকোন দুইটি বহিঃস্থ কোণের সমষ্টি দুই সমকোণ বা ১৮০° অপেক্ষা বৃহত্তর।
10. ত্রিভুজের যেকোন দুই বাহুর দৈর্ঘ্যের সমষ্টি এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর।
11. বিষমবাহু ত্রিভুজের পরিকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমরেখ।
12. বিষমবাহু ত্রিভুজের মধ্যমাত্রয়ের ছেদ বিন্দুকে ভরকেন্দ্র (centroid) বলে।
13. বিষমবাহু ত্রিভুজের শীর্ষকোণ তিনটির সমদ্বিখণ্ডকগুলো পরস্পর যে বিন্দুতে ছেদ করে তাকে অন্তঃকেন্দ্র (incenter) বলে।
14. বিষমবাহু △ABC -এর বাহুগুলোর দৈর্ঘ্য a,b,c এর উপর অঙ্কিত মধ্যমা যথাক্রমে d,e,f হলে,
    d² = 2(b² + c²) - a²4
    e² = 2(c² + a²) - b²4
    f² = 2(a² + b²) - c²4
15. ত্রিভুজ ABC এর ∠ACB একটি স্থুলকোণ হলে, AB² > AC² + BC².
16. বিষমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য জানা থাকলে এর ক্ষেত্রফল নির্ণয় করা যায়।
17. ত্রিভুজ ABC এর ∠B ও ∠C এর সমদ্বিখণ্ডকদ্বয় পরস্পর O বিন্দুতে মিলিত হলে, ∠BOC = ৯০° + ১২ ∠A.
18. ত্রিভুজ ABC এর BC বাহুর উপর লম্ব AD এবং AC বাহুর উপর লম্ব BE হলে, BC.CD = AC.CE.
19. বিষমবাহু ত্রিভুজের তিনটি বাহু পরস্পর অসমান বলে যেকোন বাহুর মধ্যমা সংশ্লিষ্ট ঐ বাহুর উপর লম্ব হতে পারে না।
20. ত্রিভুজ ABC এর ∠ACB একটি সমকোণ হলে, AB² = AC² + BC².
21. ত্রিভুজের মধ্যমাত্রয়ের সমষ্টি তার পরিসীমা অপেক্ষা ক্ষুদ্রতর।
22. ত্রিভুজ ABC এর BC বাহুর মধ্যবিন্দু D হলে, AB + AC > 2AD.
23. ত্রিভুজ ABC এর BC বাহু P এবং Q বিন্দুতে সমান তিনটি অংশে বিভক্ত হলে, AB² + AC² = AP² + AQ² + 4PQ².
24. বিষমবাহু ত্রিভুজের ভরকেন্দ্র, অন্তঃকেন্দ্র, পরিকেন্দ্র, ও লম্বকেন্দ্র চারটি ভিন্ন বিন্দু।
25. বিষমবাহু △ ABC -এর BC বাহুর মধ্যমা AD হলে, AB² + BC² = 2(AD² + BD²).
26. বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a,b,c একক হলে, পরিসীমা 2s = a + b + c একক।
27. বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a,b,c একক, অর্ধ-পরিসীমা s একক এবং ক্ষেত্রফল A বর্গ একক হলে, A = √s (s - a) (s - b) (s - c) বর্গ একক।
28. বিষমবাহু ত্রিভুজ ABC -এ ∠B = ১২০° হলে, AC² = AB² + BC² + AB.BC.
29. বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a,b,c একক, c বাহুর বিপরীত কোণ ৯০° এবং মধ্যমা তিনটির দৈর্ঘ্য d,e,f একক হলে, 2(d² + e² + f²) = 3c².
30. বিষমবাহু ত্রিভুজের যেকোন সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য a ও b একক এবং তাদের অন্তর্ভূক্ত কোণ θ এবং ক্ষেত্রফল A বর্গ একক হলে, A = 12 ab sinθ বর্গ একক।
31. বিষমবাহু ত্রিভুজের যে তিনটি বহিঃবৃত্ত আঁকা যায়, তারা (বৃত্ত তিনটি) পরস্পর অসমান।
32. ত্রিভুজ ABC এর ∠ACB একটি সূক্ষ্মকোণ হলে, AB² < AC² + BC².
33. বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a,b,c এর উপর অঙ্কিত মধ্যমা যথাক্রমে d,e,f হলে, 3(a² + b² + c²) = 4(d² + e² + f²).
34. বিষমবাহু সমকোণী ত্রিভুজের মধ্যমাত্রয়ের উপর অঙ্কিত বর্গক্ষেত্রসমূহের ক্ষেত্রফলের সমষ্টির দ্বিগুণ, অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের তিনগুণের সমান।
35. বিষমবাহু △PQR -এর মধ্যমাদ্বয় PA ও QB পরস্পর O বিন্দুতে ছেদ করলে, PQ + PR > QO + RO.
36. ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর বিপরীত অন্তঃস্থ কোণ দুইটির প্রত্যেকটি অপেক্ষা বৃহত্তর।
37. বিষমবাহু ত্রিভুজের বাহুগুলোর লম্বসমদ্বিখণ্ডক তিনটি পরস্পর যে বিন্দুতে ছেদ করে তাকে পরিকেন্দ্র (circumcenter) বলে।
38. ত্রিভুজ ABC এর AC ও AB বাহুর উপর যথাক্রমে BE ও CF লম্ব হলে, △ABC : △AEF = AB² : AE².
39. ত্রিভুজ ABC -এ AB > AC এবং ∠A এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করলে, ∠ADB একটি স্থুলকোণ হয়।
40. ত্রিভুজের যেকোন দুই বাহুর দৈর্ঘ্যের অন্তর এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা ক্ষুদ্রতর।
41. বিষমবাহু ত্রিভুজের শীর্ষ থেকে বিপরীত বাহুগুলোর উপর অঙ্কিত লম্বতিনটির দৈর্ঘ্য পরস্পর অসমান।
42. ABC এর পরিবৃত্তস্থ যেকোন বিন্দু P থেকে BC ও CA বাহুর উপর যথাক্রমে PD ও PE লম্ব এবং ED রেখাংশ AB কে O বিন্দুতে ছেদ করলে, PO রেখা AB এর উপর লম্ব অর্থাৎ PO ⊥ AB.
43. বিষমবাহু ত্রিভুজের ভরকেন্দ্র মধ্যমাকে শীর্ষ থেকে ভূমির দিকে 2:1 অনুপাতে বিভক্ত করে।
44. বিষমবাহু ত্রিভুজ ABC এর ∠B = ৬০° হলে, AC² = AB² + BC² - AB.BC.
45. বিষমবাহু ত্রিভুজের যেকোন মধ্যমা ত্রিভুজটিকে দুইটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে।
46. ত্রিভুজ ABC এর D ও E যথাক্রমে AB ও AC এর মধ্যবিন্দু এবং ∠B ও ∠C এর সমদ্বিখণ্ডকদ্বয় পরস্পর O বিন্দুতে মিলিত হলে, DE ∥ BC এবং DE = 12 BC.
47. বিষমবাহু ত্রিভুজের মধ্যমাত্রয়, বাহুগুলোর লম্বসমদ্বিখণ্ডকত্রয়, কোণগুলোর সমদ্বিখণ্ডকত্রয় এবং লম্বত্রয় চারটি ভিন্ন রেখাংশ।
48. বিষমবাহু সমকোণী ত্রিভুজ ABC এর ∠C = ৯০° এবং BC এর মধ্যবিন্দু D হলে, AB² = AD² + 3BD².
49. বিষমবাহু ত্রিভুজের পরিকেন্দ্র থেকে শীর্ষবিন্দুতিনটির দুরত্ব পরস্পর সমান।
50. ত্রিভুজ ABC এর শীর্ষত্রয় থেকে বিপরীত বাহুগুলোর উপর লম্ব AD,BE ও CF রেখাত্রয় পরস্পর O বিন্দুতে ছেদ করলে, AO.OD = BO.OE = CO.OF.
51. বিষমবাহু △PQR -এর মধ্যমাত্রয় PA,QB,RC পরস্পর O বিন্দুতে ছেদ করলে, PA + QB + RC < PQ + QR + PR.
52. যেকোন ত্রিভুজ এর সূক্ষ্মকোণ এর বিপরীত বাহুর উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টি অপেক্ষা ঐ দুই বাহুর যেকোনে একটি ও তার উপর অপরটির লম্ব অভিক্ষেপের অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফলের দ্বিগুণ পরিমান কম।
53. ত্রিভুজ ABC এর ∠ACB একটি স্থুলকোণ, AB স্থুলকোণের বিপরীত বাহু, স্থুলকোণের সন্নিহিত বাহুদ্বয় AC ও BC এবং BC বাহুর বর্ধিতাংশের উপর AC বাহুর লম্ব অভিক্ষেপ CD হলে, AB² = AC² + BC² + 2BC.CD.
54. বিষমবাহু ত্রিভুজ ABC এর মধ্যমাত্রয় পরস্পর G বিন্দুতে মিলিত হলে, AB² + BC² + AC² = 3(GA² + GB² + GC²).
55. ত্রিভুজের যেকোন দুই বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ তৃতীয় বাহুর সমান্তরাল ও দৈর্ঘ্যে তার অর্ধেক।
56. ত্রিভুজ ABC এর ∠ACB একটি সূক্ষ্মকোণ, AB সূক্ষ্মকোণের বিপরীত বাহু, সূক্ষ্মকোণের সন্নিহিত বাহুদ্বয় AC ও BC এবং BC বাহুর উপর AC বাহুর লম্ব অভিক্ষেপ CD হলে, AB² = AC² + BC² - 2BC.CD.
57. বিষমবাহু ত্রিভুজের অন্তঃকেন্দ্র থেকে বাহুগুলোর উপর অঙ্কিত লম্বতিনটির দৈর্ঘ্য পরস্পর সমান।
58. ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণ বা ১৮০°.
59. ABC ত্রিভুজের ∠A এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে এবং ABC পরিবৃত্তকে E বিন্দুতে ছেদ করলে AD² = AB.AC - BD.DC.
60. ত্রিভুজ এর যেকোন দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টি, তৃতীয় বাহুর অর্ধেকের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল এবং ঐ দুই বাহুর সমদ্বিখণ্ডক মধ্যমার উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির দ্বিগুণ।
61. ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।
62. ত্রিভুজের লম্ববিন্দু থেকে শীর্ষের দুরত্ব, পরিকেন্দ্র থেকে ঐ শীর্ষের বিপরীত বাহুর উপর অঙ্কিত লম্ব দুরত্বের দ্বিগুনের সমান।