সামান্তরিকের সূত্র

সামান্তরিক জাতীয় সকল বস্তুর বিভিন্ন পরিমাপগুলো নির্ণয় করতে হলে সামান্তরিকের সূত্র সম্পর্কে পরিষ্কার ধারণা থাকা দরকার। সামান্তরিকের বিভিন্ন পরিমাপ বলতে এর বাহু, কোণ, ভূমি, উচ্চতা, কর্ণ, ক্ষেত্রফল, পরিসীমা ইত্যাদিকে বুঝায়। সামান্তরিকের এসব পরিমাপগুলো হিসাব করার জন্য কতকগুলো সামান্তরিকের সূত্র রয়েছে। সামান্তরিক হলো বিশেষ ধরনের একটি চতুর্ভুজ যার বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল। আবার, সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে। সামান্তরিকের এসব গুণাবলীর উপর নির্ভর করে সামান্তরিকের সূত্র গড়ে উঠেছে।

সামান্তরিকের বিভিন্ন পরিমাপগুলো বের করার জন্য সামান্তরিকের সূত্র ব্যবহার করা হয়। তবে ভিন্ন ভিন্ন পরিমাপের জন্য ভিন্ন ভিন্ন সূত্র সমূহ ব্যবহার করা হয়। সাধারণভাবে, যেসকল সামান্তরিকের সূত্র সচরাচর ব্যবহৃত হয় তা নিচে তুলে ধরা হলো।

1. সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র
2. সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র
3. সামান্তরিকের কর্ণ নির্ণয়ের সূত্র

ক্ষেত্রফল পরিমাপে সামান্তরিকের সূত্র

সামান্তরিকের ক্ষেত্রফল পরিমাপ করার জন্যে বেশ কয়েকটি সামান্তরিকের সূত্র রয়েছে। ক্ষেত্রফল পরিমাপের ঐ সূত্র সমূহ নিম্নরূপ:

1. ভূমি ও উচ্চতা সম্পর্কিত সামান্তরিকের সূত্র
2. কর্ণ ও কর্ণের উপর লম্ব সম্পর্কিত সামান্তরিকের সূত্র
3. বাহু ও অন্তর্ভূক্ত কোণ সম্পর্কিত সামান্তরিকের সূত্র

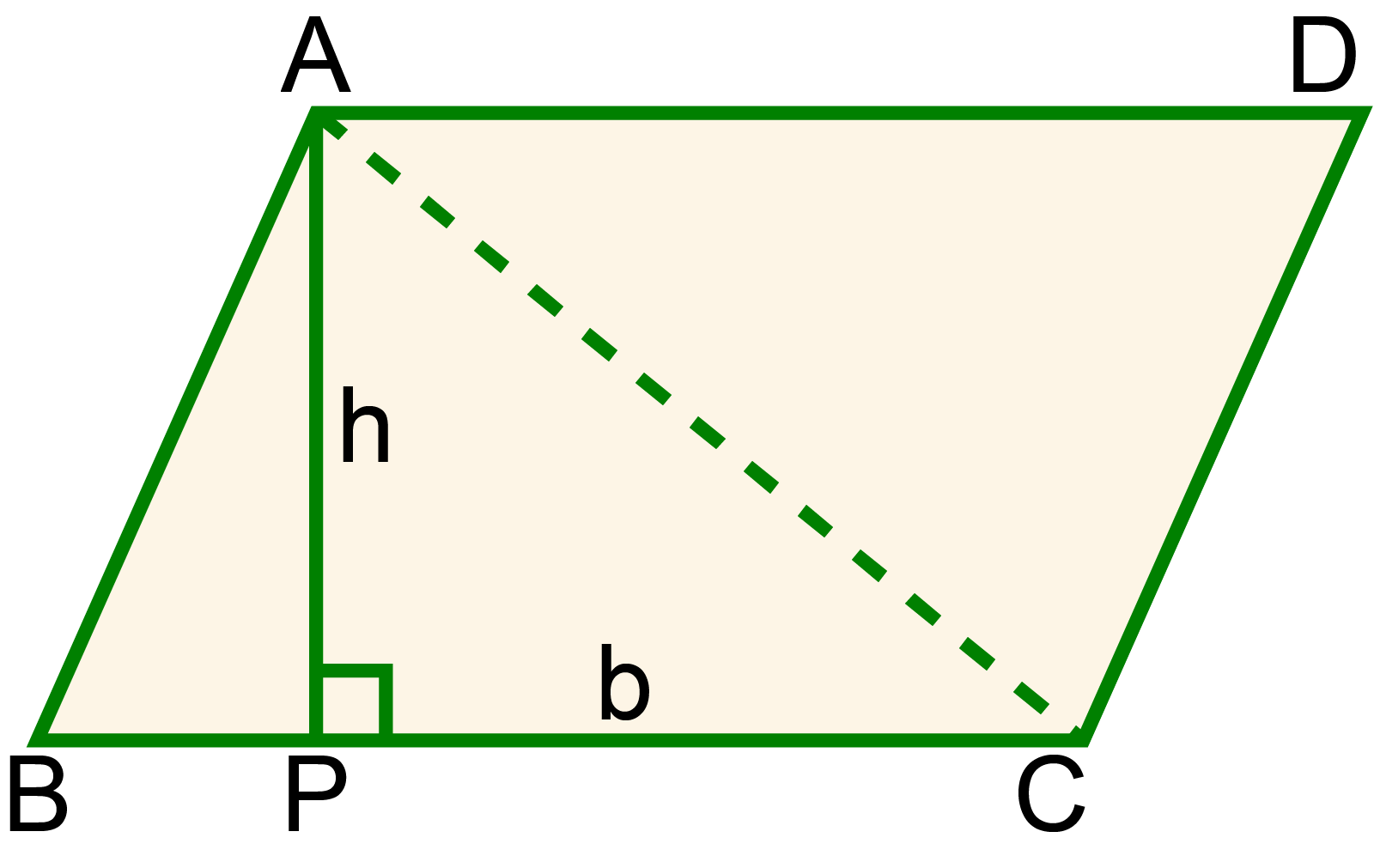
ভূমি ও উচ্চতা সম্পর্কিত সামান্তরিকের সূত্র

সামান্তরিকের ক্ষেত্রফল পরিমাপে ভূমি ও উচ্চতা সম্পর্কিত একটি সামান্তরিকের সূত্র রয়েছে। সূত্রটি নিম্নরূপ:
সামান্তরিকের ক্ষেত্রফল = ( ভূমি × উচ্চতা ) বর্গ একক।
অতএব, সামান্তরিকের ভূমি b একক এবং উচ্চতা h একক হলে,
সামান্তরিকের ক্ষেত্রফল = (b × h) বর্গ একক।

কর্ণ ও কর্ণের উপর লম্ব সম্পর্কিত সামান্তরিকের সূত্র

সামান্তরিকের কর্ণ ও শীর্ষ থেকে ঐ কর্ণের উপর লম্ব সংশ্লিষ্ট ক্ষেত্রফল পরিমাপে সামান্তরিকের সূত্র রয়েছে। ক্ষেত্রফল পরিমাপের সূত্রটি নিম্নরূপ:
সামান্তরিকের ক্ষেত্রফল = ( কর্ণ × শীর্ষ থেকে ঐ কর্ণের উপর লম্ব ) বর্গ একক।

একটি সামান্তরিকের কর্ণ d এবং শীর্ষ থেকে কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য h হলে,
সামান্তরিকের ক্ষেত্রফল = (d × h) বর্গ একক।

বাহু ও অন্তর্ভূক্ত কোণ সম্পর্কিত সামান্তরিকের সূত্র

সামান্তরিকের বাহু ও তাদের অন্তর্ভূক্ত কোণ সংশ্লিষ্ট সামান্তরিকের সূত্র ব্যবহার করে ক্ষেত্রফল পরিমাপ করা হয়। ক্ষেত্রফল পরিমাপের সূত্রটি নিম্নরূপ:

একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a একক ও b একক এবং তাদের অন্তর্ভূক্ত কোণের ‍পরিমাপ θ হলে,
সামান্তরিকের ক্ষেত্রফল = ab sinθ বর্গ একক।

সামান্তরিক উদাহরণ

পরিসীমা পরিমাপে সামান্তরিকের সূত্র

সামান্তরিকের পরিসীমা পরিমাপ করতে সামান্তরিকের সূত্র প্রয়োগ করা হয়। পরিসীমা পরিমাপের সূত্রটি নিম্নরূপ:
সামান্তরিকের পরিসীমা = 2 × (একজোড়া সন্নিহিত বাহুর সমষ্টি) একক।

কোনো সামান্তরিকের সন্নিহিত বাহু দুইটি a একক এবং b একক হলে পরিসীমা পরিমাপে সামান্তরিকের সূত্রটি নিম্নরূপ:
সামান্তরিকের পরিসীমা = 2 (a + b) একক।

কর্ণ পরিমাপে সামান্তরিকের সূত্র

সামান্তরিকের কর্ণ পরিমাপ করতেও সামান্তরিকের সূত্র ব্যবহৃত হয়। সামান্তরিকের দুইটি ভিন্ন দৈর্ঘ্যের কর্ণ রয়েছে। এদের দৈর্ঘ্য পরিমাপ করতে দুইটি আলাদা আলাদা সূত্র ব্যবহার করতে হয়।

সামান্তরিকের সন্নিহিত বাহু দুইটি a ও b এবং তাদের অন্তর্ভূক্ত কোণ θ একটি সূক্ষ্মকোণ হলে সামান্তরিকের ক্ষূদ্রতম কর্ণ নির্ণয়ের সূত্রটি হবে নিম্নরূপ:
ক্ষূদ্রতম কর্ণ = √a² + b² - 2ab cosθ

আর, বৃহত্তম কর্ণ নির্ণয়ের সূ্ত্রটি হবে নিম্নরূপ:
বৃহত্তম কর্ণ = √a² + b² + 2ab cosθ