আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র
এই টিউটোরিয়ালটি শেষে -
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র বর্ণনা করতে পারা যাবে।
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয় করতে পারা করা যাবে।
আয়তক্ষেত্রের ক্ষেত্রফল
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র তৈরি করার পূর্বে আয়তক্ষেত্রের ক্ষেত্রফল কি তা জানা দরকার। আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থের গুণফলকে আয়তক্ষেত্রের ক্ষেত্রফল বলে। অর্থাৎ, আয়তক্ষেত্রের দৈর্ঘ্যকে প্রস্থ দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়। অতএব, আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র লিখলে দাঁড়ায়,
আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক।
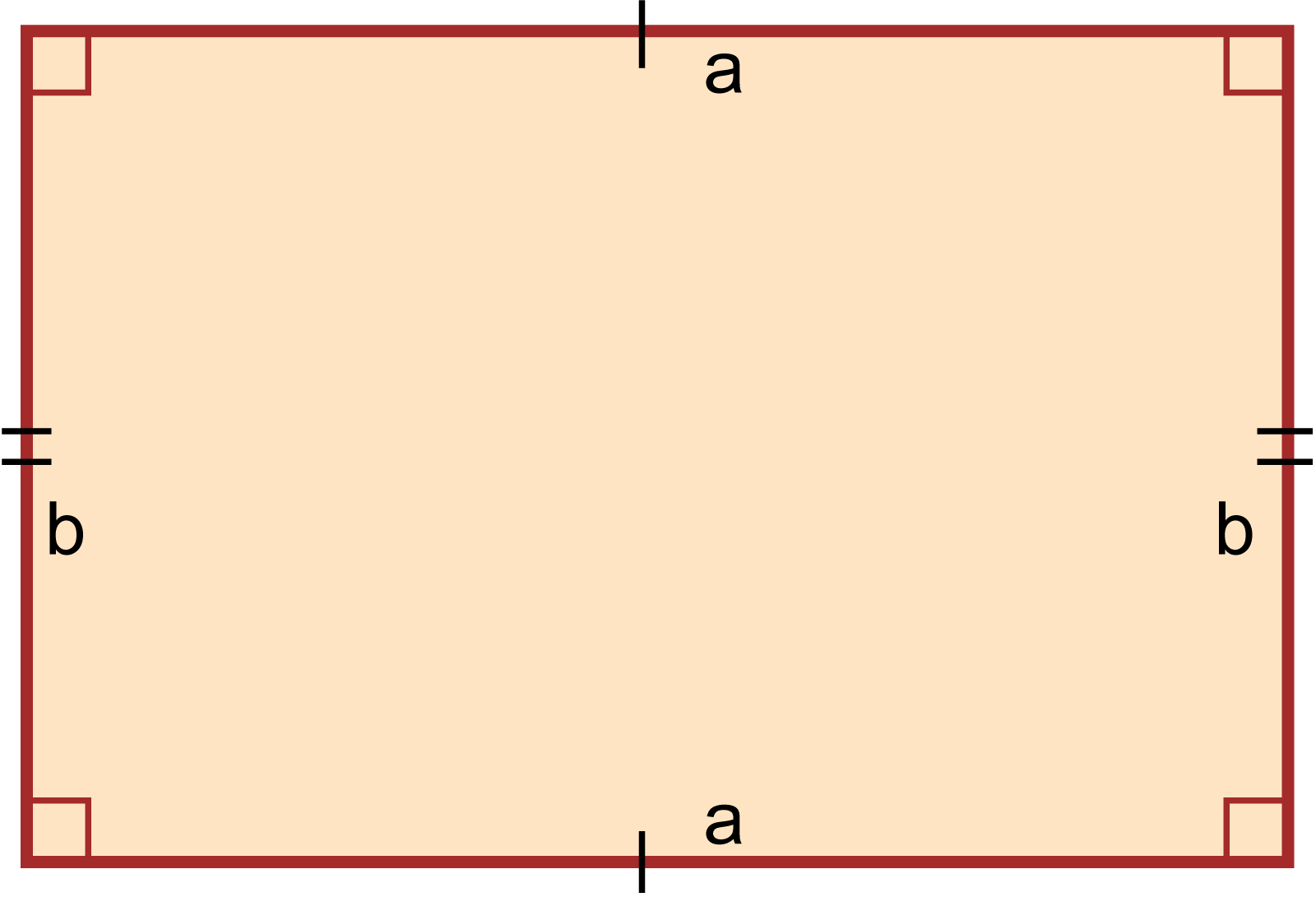
আয়তক্ষেত্রের দৈর্ঘ্য a একক, প্রস্থ b একক এবং ক্ষেত্রফল A বর্গ একক হলে আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র হবে,
আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক
অর্থাৎ, A= ab বর্গ একক।
একটি আয়তক্ষেত্রের ক্ষেত্রফল
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যবহার করে যেকোনো একটি আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয় করা যায়।
উদাহরণ ১
একটি আয়তক্ষেত্রের দৈর্ঘ্য ৩৫ সেমি ও প্রস্থ ১২ সেমি হলে ক্ষেত্রফল কত?
সমাধানঃ মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য a = ৩৫ সেমি এবং প্রস্থ b = ১২ সেমি।
এখন আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যবহার করে পাওয়া যায়,
আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক
বা, আয়তক্ষেত্রের ক্ষেত্রফল = (a × b) বর্গ একক
বা, আয়তক্ষেত্রের ক্ষেত্রফল = (৩৫ × ১২) বর্গ সেমি
∴ আয়তক্ষেত্রের ক্ষেত্রফল = ৪২০ বর্গ সেমি
উদাহরণ ২
একটি আয়তাকার ঘরের দৈর্ঘ্য ১২.৫ মি. ও প্রস্থ ৭.৫ মি. হলে ঘরটির ক্ষেত্রফল কত?
সমাধানঃ মনে করি, আয়তাকার ঘরের দৈর্ঘ্য a = ১২.৫ মি. এবং প্রস্থ b = ৭.৫ মি.।
তাহলে আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যবহার করলে দাঁড়ায়,
ঘরটির ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক
অর্থাৎ, ঘরটির ক্ষেত্রফল = (a × b) বর্গ একক
অর্থাৎ, ঘরটির ক্ষেত্রফল = (১২.৫ × ৭.৫) বর্গ মি.
∴ ঘরটির ক্ষেত্রফল = ৯৩.৭৫ বর্গ মি.
সচরাচর যেসব প্রশ্ন করা হয়ে থাকে - Frequently Asked Questions (FAQ)
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র বিষয়ক সচরাচর যেসব প্রশ্নসমূহ মানুষ করে থাকে।
উত্তরঃ আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক
উত্তরঃ আয়তক্ষেত্রের দৈর্ঘ্য a একক এবং প্রস্থ b একক হলে আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র হবে (দৈর্ঘ্য × প্রস্থ) বর্গ একক অর্থাৎ, আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক।
∴ আয়তক্ষেত্রের ক্ষেত্রফল = ab বর্গ একক।
উত্তরঃ আয়তক্ষেত্রের ক্ষেত্রফল বলতে আয়তক্ষেত্রের চারটি বাহু দ্বারা বেষ্টিত তলকে বুঝায়। আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক। উদাহরণস্বরূপ, একটি আয়তক্ষেত্রের দৈর্ঘ্য ৬ সেমি ও প্রস্থ ৫ সেমি হলে,
ক্ষেত্রফল = (৬ × ৫) বর্গ সেমি।
∴ আয়তক্ষেত্রের ক্ষেত্রফল = ৩০ বর্গ সেমি।
উত্তরঃ আয়তক্ষেত্রের সূত্র বলতে আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র, আয়তক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র, আয়তক্ষেত্রের কর্ণের সূত্র ইত্যাদিকে বুঝায়।
আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক।
আয়তক্ষেত্রের পরিসীমা= ২ × (দৈর্ঘ্য + প্রস্থ) একক।
আয়তক্ষেত্রের কর্ণ= √(দৈর্ঘ্য)2+ (প্রস্থ)2 একক।
∴ একটি আয়তক্ষেত্রের দৈর্ঘ্য a একক এবং প্রস্থ b একক হলে, আয়তক্ষেত্রের কর্ণ= √a2+b2 একক।
উত্তরঃ আয়তক্ষেত্রের পরিসীমা বলতে এর চার বাহুর দৈর্ঘ্যের সমষ্টিকে বুঝায়। সুতরাং, আয়তক্ষেত্রের পরিসীমা = ২ × (দৈর্ঘ্য + প্রস্থ) একক। একটি আয়তক্ষেত্রের দৈর্ঘ্য a একক এবং প্রস্থ b একক হলে,
আয়তক্ষেত্রের পরিসীমা = ২ × (a + b) একক।
উত্তরঃ আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক এবং বর্গক্ষেত্রের ক্ষেত্রফল = (বাহু × বাহু) বর্গ একক। একটি আয়তক্ষেত্রের দৈর্ঘ্য a একক এবং প্রস্থ b একক হলে,
আয়তক্ষেত্রের ক্ষেত্রফল = ab বর্গ একক।
একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a একক হলে,
বর্গক্ষেত্রের ক্ষেত্রফল = a2 বর্গ একক।