সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র
এই টিউটোরিয়ালটি শেষে ...
সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যাখ্যা করতে পারা যাবে।
সামান্তরিকের ক্ষেত্রফল নির্ণয় করতে পারা যাবে।
সামান্তরিক জাতীয় বস্তুর ক্ষেত্রফল বের করতে হলে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র ভালভাবে জানা থাকা দরকার। সামান্তরিক হলো বিশেষ ধরনের একটি চতুর্ভুজ যার বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল। একটি সামান্তরিক তার চারটি বাহু দ্বারা যতটুকু জায়গা বা সমতল দখল করে থাকে সেটাই তার ক্ষেত্রফল। সামান্তরিকের অভ্যন্তরের এ জায়গা বা ক্ষেত্রফল পরিমাপ করার জন্যে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যবহার করা হয়।
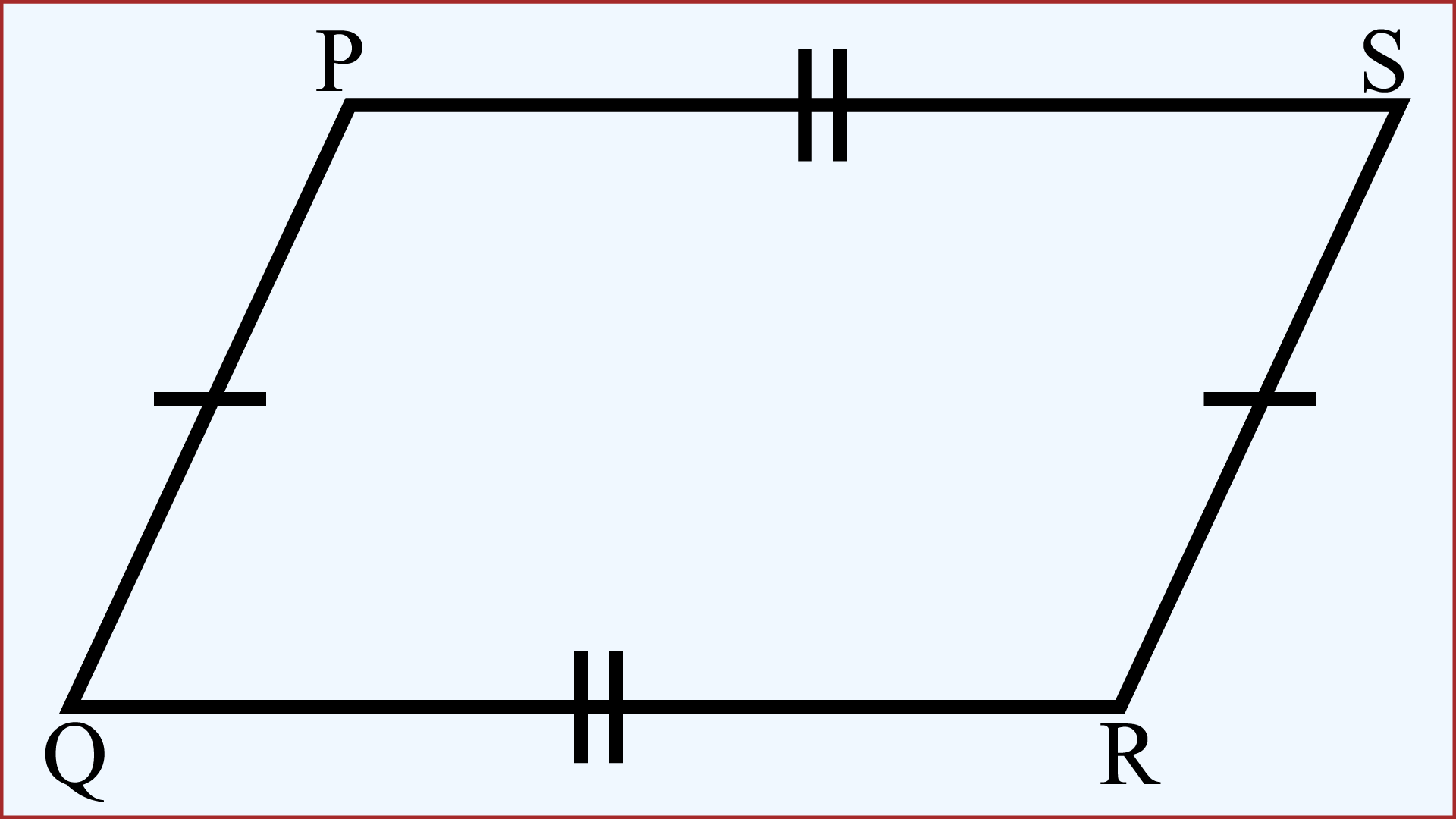
সামান্তরিকের ক্ষেত্রফল নির্ণয় করার করার জন্যে একাধিক পদ্ধতি ও সূত্র রয়েছে। এসব পদ্ধতিতে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র উদ্ভাবন করে এর ক্ষেত্রফল পরিমাপ করা হয়।
ভূমি ও উচ্চতার ভিত্তিতে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র
সামান্তরিকের ক্ষেত্রফল নির্ণয় করার জন্য ভূমি ও উচ্চতা সম্পর্কিত সূত্রটি সবচেয়ে সহজ ও বহুল প্রচলিত। সামান্তরিকের ভূমিকে এর উচ্চতা দিয়ে গুণ করলে ক্ষেত্রফল পাওয়া যায়।
∴ সামান্তরিকের ক্ষেত্রফল = ( ভূমি × উচ্চতা ) বর্গ একক।
মনে করি, একটি সামান্তরিকের ভূমি b এবং উচ্চতা h.
তাহলে, সামান্তরিকের ক্ষেত্রফল = ( ভূমি × উচ্চতা ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল = (b × h) বর্গ একক
কিন্তু, যদি বলা হয় সামান্তরিকের ভূমিকে উচ্চতা দিয়ে গুণ করলে কেন বা কিভাবে এর ক্ষেত্রফল পাওয়া যায়? তাহলে দেখা যাক, এখন এই সূত্রটি উদ্ভাবন করা যায় কিনা!
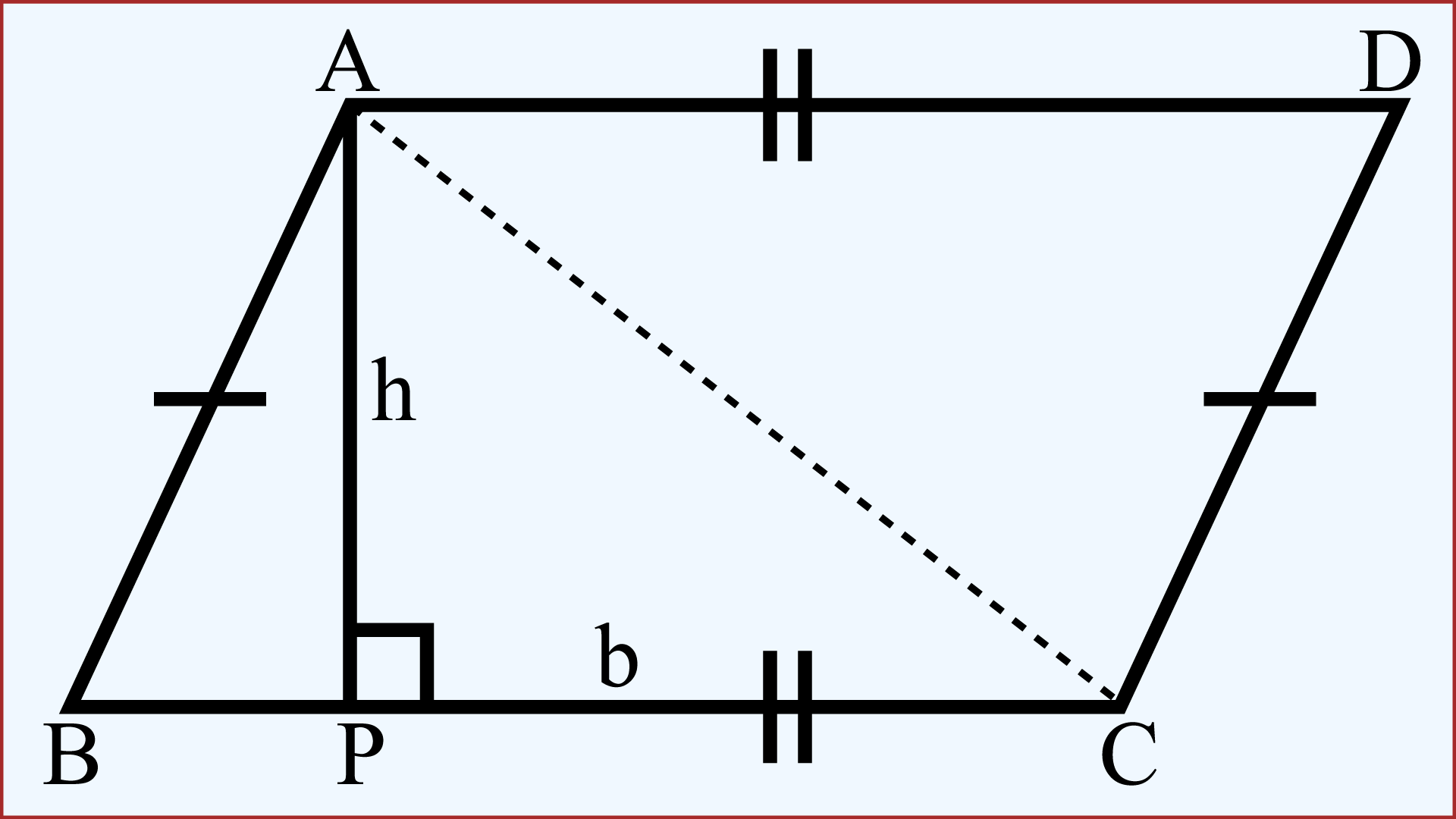
মনে করি, ABCD একটি সামান্তরিক।
সামান্তরিকটির শীর্ষবিন্দু A থেকে ভূমির উপর একটি লম্ব AP আঁকি অর্থাৎ, AP⊥BC আঁকি যেখানে AP = h এবং BC = b.
AC কর্ণ আঁকি।
আবার সামান্তরিকের কর্ণ সামান্তরিকটিকে দুইটি সর্বসম ত্রিভূজে বিভক্ত করে। ∴ ꕔABC ≅ ꕔACD.
এখন, ▱ABCD = △ABC + △ACD
বা, ▱ABCD = △ABC+△ABC [∵ △ABC ≅ △ACD]
বা, ▱ABCD = 2.△ABC
বা, ▱ABCD = 2 × 12 × BC.AP [∵ △ABC = 12 × ভূমি × উচ্চতা]
বা, ▱ABCD = BC.AP
∴ ▱ABCD = bh
∴ সামান্তরিকের ক্ষেত্রফল = ( ভূমি × উচ্চতা ) বর্গ একক (প্রমাণিত)।
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক
সামান্তরিকের ভূমি b একক এবং উচ্চতা h একক হলে,
সামান্তরিকের ক্ষেত্রফল = (b × h) বর্গ একক।
উদাহরণ ১: একটি সামান্তরিকের ভূমি ২৪ সেমি এবং উচ্চতা ১৬ সেমি হলে সামান্তরিকের ক্ষেত্রফল নির্ণয় করতে হবে।
উত্তর: মনেকরি, সামান্তরিকটির ভূমি b = ২৪ সেমি এবং উচ্চতা h = ১৬ সেমি।
আমরা জানি,
সামান্তরিকের ক্ষেত্রফল = ( ভূমি × উচ্চতা ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল = ( b × h ) বর্গ একক।
বা, সামান্তরিকের ক্ষেত্রফল = ( ২৪ × ১৬ ) বর্গ সেমি।
∴ সামান্তরিকের ক্ষেত্রফল = ৩৮৪ বর্গ সেমি।
কর্ণ ও কর্ণের উপর লম্বের ভিত্তিতে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র
কোনো সামান্তরিকের ভূমি ও উচ্চতা দেওয়া থাকলে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যবহার করে কিভাবে ক্ষেত্রফল পরিমাপ করা যায় এতক্ষণ তা আমরা শিখলাম। কিন্তু যদি সামান্তরিকের কর্ণ ও ঐ কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য দেওয়া থাকে তাহলে কিভাবে এর ক্ষেত্রফল পরিমাপ করবো?
সামান্তরিকের ক্ষেত্রফল পরিমাপ করতে কর্ণ ও কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য সংশ্লিষ্ট সূত্রটিও এর ক্ষেত্রফল পরিমাপ করার জন্য ব্যবহৃত হয়।
সামান্তরিকের যেকোনো একটি কর্ণকে ঐ কর্ণের বিপরীত শীর্ষ বিন্দু থেকে উক্ত কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়। তাহলে, সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র দাঁড়ায়,
সামান্তরিকের ক্ষেত্রফল =( কর্ণ × শীর্ষ থেকে কর্ণের উপর লম্ব ) বর্গ একক।
মনে করি, একটি সামান্তরিকের কর্ণ d এবং শীর্ষ থেকে কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য h.
তাহলে, সামান্তরিকের ক্ষেত্রফল =( কর্ণ × শীর্ষ থেকে কর্ণের উপর লম্ব ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল = (d × h) বর্গ একক।
এখন প্রশ্ন হলো, সামান্তরিকের কর্ণকে ঐ কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায় কেন? তাহলে দেখা যাক, সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র উদ্ভাবন করা যায় কিনা!
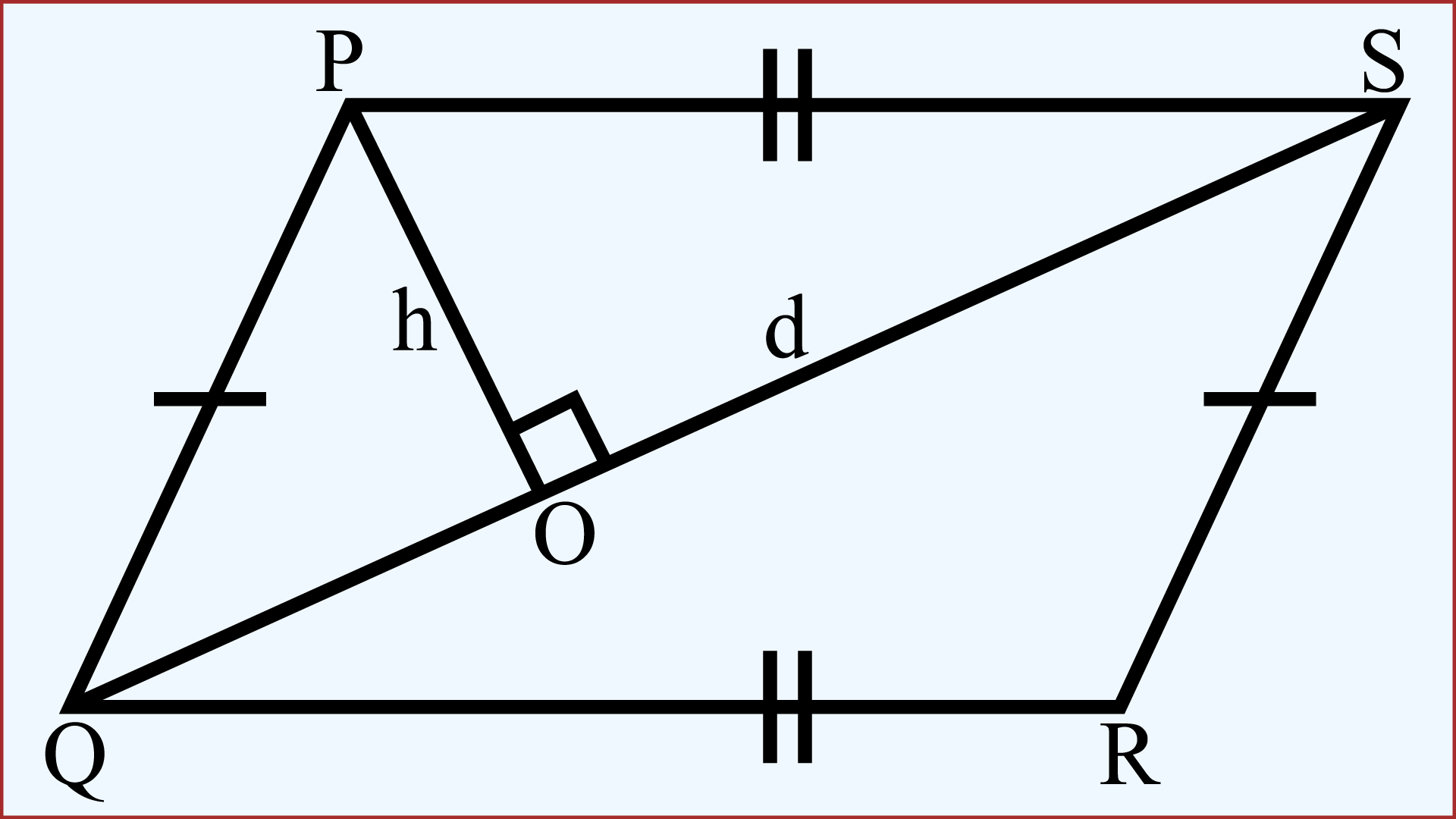
চিত্রে, PQRS একটি সামান্তরিক এবং QS একটি কর্ণ।
সামান্তরিকটির শীর্ষ বিন্দু P থেকে কর্ণ QS উপর একটি লম্ব PO আঁকি অর্থাৎ, PO⊥QS আঁকি যেখানে PO = h এবং QS = d.
আবার, সামান্তরিকের কর্ণ সামান্তরিকটিকে দুইটি সর্বসম ত্রিভূজে বিভক্ত করে।
তাহলে, PQRS সামান্তরিকের QS কর্ণ সামান্তরিকটিকে দুইটি সর্বসম ত্রিভূজে বিভক্ত করে। ∴ ꕔPQS ≅ ꕔQRS.
এখন, ▱PQRS = △PQS + △QRS
বা, ▱PQRS = △PQS + △PQS [∵ △PQS ≅ △QRS]
বা, ▱PQRS = 2×△PQS
বা, ▱PQRS = 2 × 12 × ভূমি × উচ্চতা
বা, ▱PQRS = 2 × 12 × QS × PO
বা, ▱PQRS = QS × PO
∴ সামান্তরিকের ক্ষেত্রফল =( কর্ণ × শীর্ষ থেকে কর্ণের উপর লম্ব ) বর্গ একক (প্রমাণিত)।
সামান্তরিকের ক্ষেত্রফল = ( কর্ণ × শীর্ষ থেকে কর্ণের উপর লম্ব ) বর্গ একক।
উদাহরণ ২: একটি সামান্তরিকের একটি কর্ণের দৈর্ঘ্য ৯৬ সেমি এবং বিপরীত শীর্ষবিন্দু কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য ৪৮ সেমি হলে সামান্তরিকটির ক্ষেত্রফল নির্ণয় করতে হবে।
উত্তর: মনেকরি, সামান্তরিকটির একটি কর্ণের দৈর্ঘ্য d = ৯৬ সেমি এবং বিপরীত শীর্ষবিন্দু কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য h = ৪৮ সেমি।
আমরা জানি,
সামান্তরিকের ক্ষেত্রফল = ( কর্ণ × শীর্ষ থেকে কর্ণের উপর লম্ব ) বর্গ একক।
বা, সামান্তরিকের ক্ষেত্রফল = ( d × h ) বর্গ একক।
বা, সামান্তরিকের ক্ষেত্রফল = ( ৯৬ × ৪৮ ) বর্গ সেমি।
∴ সামান্তরিকের ক্ষেত্রফল = ৪৬০৮ বর্গ সেমি।
সন্নিহিত বাহু ও অন্তর্ভূক্ত কোণের ভিত্তিতে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র
সামান্তরিকের ক্ষেত্রফল পরিমাপ করতে সন্নিহিত বাহু ও তাদের অন্তর্ভূক্ত কোণ সম্পর্কিত সূত্রটি ব্যবহার করে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র তৈরি করা যায়; অতপর তা প্রয়োগ করে এর ক্ষেত্রফল পরিমাপ করা যায়।
সামান্তরিকের যেকোনো দুইটি সন্নিহিত বাহুর দৈর্ঘ্যের গুণফলকে তাদের অন্তর্ভূক্ত কোণের sin অনুপাত দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়।
মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a একক ও b একক এবং তাদের অন্তর্ভূক্ত কোণের পরিমাপ θ।
তাহলে, সামান্তরিকের ক্ষেত্রফল = ( সন্নিহিত বাহুর গুণফল × sinθ ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল = ab sinθ বর্গ একক।
তাহলে দেখা যাক, সন্নিহিত বাহু ও তাদের অন্তর্ভূক্ত কোণ সম্পর্কিত সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র কিভাবে উৎপন্ন হয়।
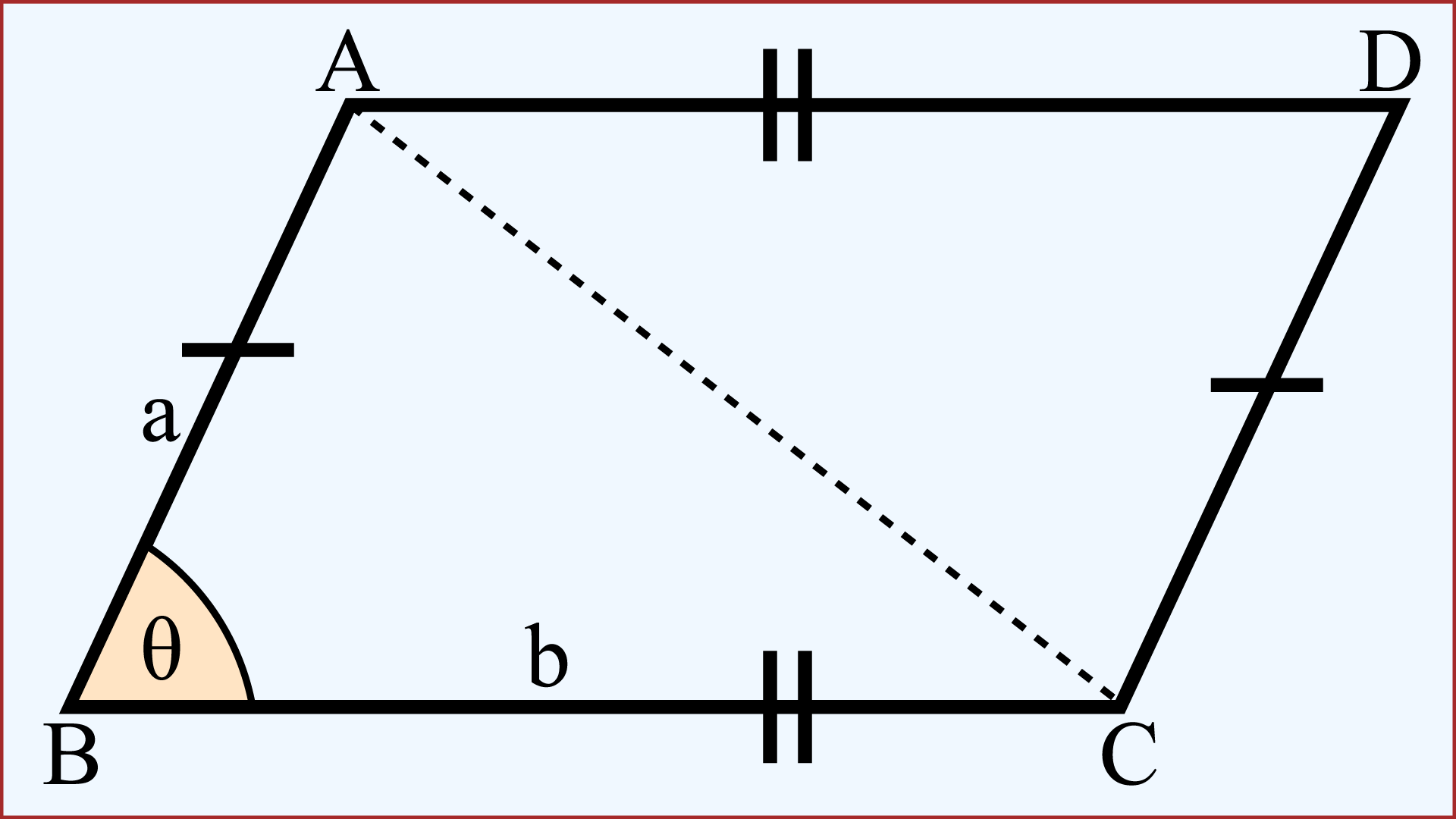
চিত্রে, ABCD সামান্তরিকের AB = CD = a এবং BC = AD = b। AC একটি কর্ণ আঁকি।
আবার, সামান্তরিকের কর্ণ সামান্তরিকটিকে দুইটি সর্বসম ত্রিভূজে বিভক্ত করে।
তাহলে, AC কর্ণ ABCD সামান্তরিকটিকে দুইটি সর্বসম ত্রিভূজে বিভক্ত করে। ∴ ꕔABC ≅ ꕔACD.
এখন, ▱ABCD = △ABC + △ACD
বা, ▱ABCD = △ABC + ꕔABC [∵ △ABC ≅ △ACD]
বা, ▱ABCD = 2×△ABC
বা, ▱ABCD = 2 × 12 × ab sinθ [∵ △ABC = 12 × ab sinθ]
∴ ▱ABCD = ab sinθ
∴ সামান্তরিকের ক্ষেত্রফল = ab sinθ বর্গ একক (প্রমাণিত)।
একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a একক ও b একক এবং তাদের অন্তর্ভূক্ত কোণের পরিমাপ θ হলে,
সামান্তরিকের ক্ষেত্রফল = ab sinθ বর্গ একক।
বাহু ও কোণের ভিত্তিতে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের এ্যাপ
পরিসীমাঃ
ক্ষেত্রফলঃ
প্রথমে বাটন নির্বাচন; অতপরঃ নিচের ডানদিকের লাল অংশ ড্রাগ করলে পরিবর্তন লক্ষ্য করা যায়।
উদাহরণ ৩: একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য 40 সেমি ও 35 সেমি এবং তাদের অন্তর্ভূক্ত কোণের পরিমাপ 30° হলে সামান্তরিকটির ক্ষেত্রফল নির্ণয় করতে হবে।
উত্তর: মনেকরি, সামান্তরিকটির সন্নিহিত বাহু দুইটির দৈর্ঘ্য a = 40 সেমি ও b = 35 সেমি এবং তাদের অন্তর্ভূক্ত কোণের পরিমাপ θ = 30°।
আমরা জানি,
সামান্তরিকের ক্ষেত্রফল = ab sinθ বর্গ একক
বা, সামান্তরিকের ক্ষেত্রফল = ( 40 × 35 × sin30° ) বর্গ সেমি।
বা, সামান্তরিকের ক্ষেত্রফল = ( 40 × 35 × 12 ) বর্গ সেমি।
বা, সামান্তরিকের ক্ষেত্রফল = ( 20 × 35 ) বর্গ সেমি।
∴ সামান্তরিকের ক্ষেত্রফল = 700 বর্গ সেমি।
সচরাচর যেসব প্রশ্ন করা হয়ে থাকে - Frequently Asked Questions (FAQ)
সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র বিষয়ক আরও যেসব প্রশ্নসমূহ সচরাচর মানুষ করে থাকে।
যে সূত্র প্রয়োগ করে সামান্তরিকের ক্ষেত্রফল নির্ণয় করা হয় তাই সামান্তরিকের ক্ষেত্রফলের সূত্র। সামান্তরিকের ভূমিকে উচ্চতা দ্বারা গুণ করলে সামান্তরিকের ক্ষেত্রফল পাওয়া যায়। অতএব, সামান্তরিকের ক্ষেত্রফলের সূত্রটি হবে নিম্নরূপ:
সামান্তরিকের ক্ষেত্রফল = ( ভূমি × উচ্চতা ) বর্গ একক।
সামান্তরিকের যেকোনো সন্নিহিত বাহু দুইটির গুণফলকে তাদের অন্তর্গত কোণের sin অনুপাত দ্বারা গুণ করলে ঐ সামান্তরিকের ক্ষেত্রফল পাওয়া যায়। একটি সামান্তরিকের সন্নিহিত বাহদ্বয়ের দৈর্ঘ্য a ও b একক এবং তাদের অন্তর্গত কোণের মান θ হলে এর ক্ষেত্রফল হবে নিম্নরূপ:
সামান্তরিকের ক্ষেত্রফল =( ab sinθ ) বর্গ একক।
সামান্তরিকের যেকোনো সন্নিহিত বাহুদ্বয়ের সমষ্টিকে দ্বিগুণ করলে সামান্তরিকের পরিসীমা পাওয়া যায়। সুতরাং, সামান্তরিকের পরিসীমা = ২ × (একজোড়া সন্নিহিত বাহুদ্বয়ের সমষ্টি) একক। তাহলে, সামান্তরিকের সন্নিহিত বাহদ্বয়ের দৈর্ঘ্য a ও b একক হলে
সামান্তরিকের পরিসীমা = 2( a + b) একক।
সামান্তরিকের যেকোনো একটি কর্ণকে ঐ কর্ণের বিপরীত শীর্ষবিন্দু থেকে উক্ত কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য দ্বারা গুণ করলে সামান্তরিকের ক্ষেত্রফল পাওয়া যায়।
সুতরাং, সামান্তরিকের ক্ষেত্রফল = ( কর্ণ × কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য ) বর্গ একক।
সামান্তরিকের ক্ষেত্রফল নির্ণয়ের একাধিক পদ্ধতি ও সূত্র। সামান্তরিকের এসব সূত্রসমূহ সামান্তরিকের ভূমি, উচ্চতা, কর্ণ, সন্নিহিত বাহু, কোণ ইত্যাদির উপর ভিত্তি করে উৎপত্তি হয়।
- সামান্তরিকের ভূমি ও উচ্চতার ভিত্তিতে সামান্তরিকের ক্ষেত্রফল = ( ভূমি × উচ্চতা ) বর্গ একক। কোনো সামান্তরিকের ভূমি b ও উচ্চতা h হলে,
সামান্তরিকের ক্ষেত্রফল = bh বর্গ একক। - সামান্তরিকের কর্ণ ও ঐ কর্ণের বিপরীত কৌণিক বিন্দু থেকে উক্ত কর্ণের উপর অংকিত লম্বের দৈর্ঘ্যের ভিত্তিতে সামান্তরিকের ক্ষেত্রফল = ( কর্ণ × কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য ) বর্গ একক। সুতরাং, একটি সামান্তরিকের একটি কর্ণের দৈর্ঘ্য d ও উক্ত কর্ণের উপর অংকিত লম্বের দৈর্ঘ্য h হলে
সামান্তরিকের ক্ষেত্রফল = dh বর্গ একক। - একটি সামান্তরিকের একজোড়া সন্নিহিত বাহু দুইটি a একক ও b একক এবং এদের অন্তর্ভূক্ত কোণের পরিমাপ θ হলে,
সামান্তরিকের ক্ষেত্রফল =( ab sinθ ) বর্গ একক।