সামান্তরিকের কর্ণ নির্ণয়ের সূত্র
এই টিউটোরিয়ালটি শেষে ...
সামান্তরিকের কর্ণ নির্ণয়ের সূত্র ব্যাখ্যা করতে পারা যাবে।
সামান্তরিকের কর্ণের দৈর্ঘ্য নির্ণয় করতে পারা যাবে।
সামান্তরিক আকৃতির কোনো বস্তুর কর্ণ পরিমাপ করতে হলে সামান্তরিকের কর্ণ নির্ণয়ের সূত্র সম্পর্কে ভালভাবে জানা থাকা দরকার। একটি সামান্তরিকের কর্ণ হলো যেকোনো দুইটি বিপরীত কোণিক বিন্দুর দূরত্ব। আরও ভালভাবে বললে, একটি সামান্তরিকের যেকোনো দুইটি বিপরীত কোণিক বিন্দুর সংযোজক রেখাংশ হলো এর কর্ণ। আর এই কর্ণ পরিমাপ করতে সামান্তরিকের কর্ণ নির্ণয়ের সূত্র ব্যবহার করা হয়। সামান্তরিক হলো এমন একটি চতুর্ভুজ যার বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল। আবার এর প্রত্যেক জোড়া বিপরীত কোণ দুইটিও পরস্পর সমান। সামান্তরিকের কর্ণ নির্ণয়ের সূত্র প্রয়োগ করে এর কর্ণ দুইটির দৈর্ঘ্য পরিমাপ করা হয়।
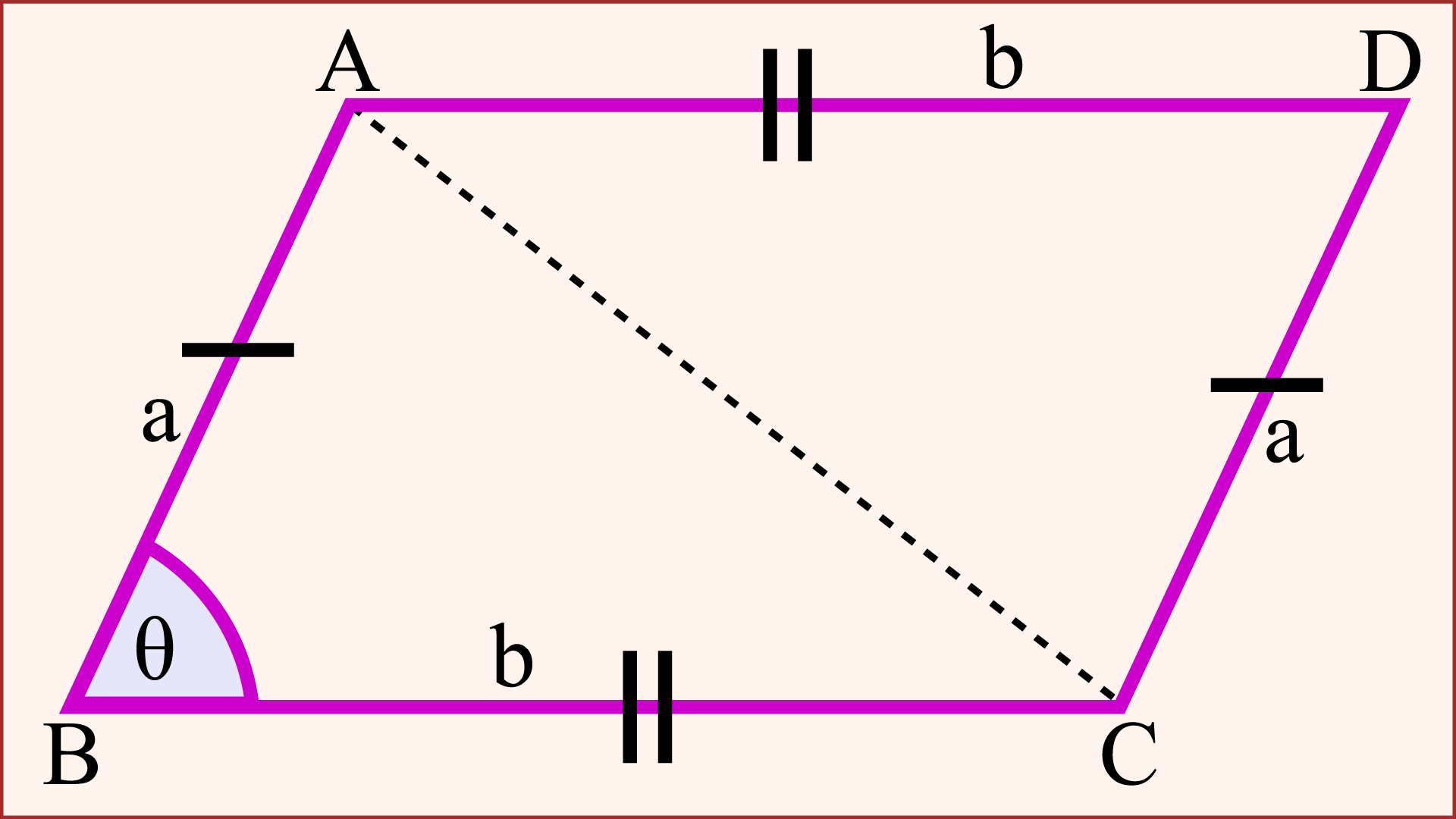
লক্ষ্য করি, সামান্তরিকের দুই জোড়া বিপরীত কোণ রয়েছে। এক জোড়া বিপরীত কোণের প্রত্যেকটি সূক্ষ্মকোণ। আর, অন্যজোড়া বিপরীত কোণের প্রত্যেকটি স্থুলকোণ। সূক্ষকোণদ্বয়ের শীর্ষ বিন্দু দুইটি পরস্পর যোগ করলে বৃহত্তম কর্ণ তৈরি হয়। আবার, স্থূলকোণদ্বয়ের শীর্ষ বিন্দু দুইটি পরস্পর যোগ করলে ক্ষূদ্রতম কর্ণ উৎপন্ন হয়। আর সামান্তরিকের কর্ণ নির্ণয়ের সূত্র ব্যবহার করে এই কর্ণ দুইটির দৈর্ঘ্য পরিমাপ করা যায়।
মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটি a ও b এবং তাদের অন্তর্ভূক্ত কোণ θ, যা একটি সূক্ষ্মকোণ। তাহলে, সামান্তরিকের কর্ণ নির্ণয়ের সূত্র ব্যবহার করে এর ক্ষূদ্রতম কর্ণ নির্ণয় করা যায়। আর সূত্রটি হবে,
ক্ষূদ্রতম কর্ণ = √a2 + b2 - 2ab cosθ
উপরের চিত্রে, ABCD সামান্তরিকের AB = CD = a এবং BC = AD = b। ∠A ও ∠C দুইটি স্থূলকোণ। এই কোণ দুইটির শীর্ষবিন্দু পরস্পর যোগ করলে ক্ষূদ্রতম কর্ণ AC উৎপন্ন হয়। আবার, a ও b বাহু দুইটির অন্তর্ভূক্ত কোণ ∠B = θ, যা একটি সূক্ষ্মকোণ। তাহলে, সামান্তরিকের কর্ণ নির্ণয়ের সূত্র প্রয়োগ করে ক্ষূদ্রতম কর্ণটির দৈর্ঘ্য বের করা যায় এবং সূত্রটি হবে,
ক্ষূদ্রতম কর্ণ AC = √a2 + b2 - 2ab cosθ
সামান্তরিকের সন্নিহিত বাহু দুইটি a ও b এবং তাদের অন্তর্ভূক্ত কোণ θ একটি সূক্ষ্মকোণ হলে সামান্তরিকের ক্ষূদ্রতম কর্ণ নির্ণয়ের সূত্রটি হবে নিম্নরূপ:
ক্ষূদ্রতম কর্ণ = √a2 + b2 - 2ab cosθ
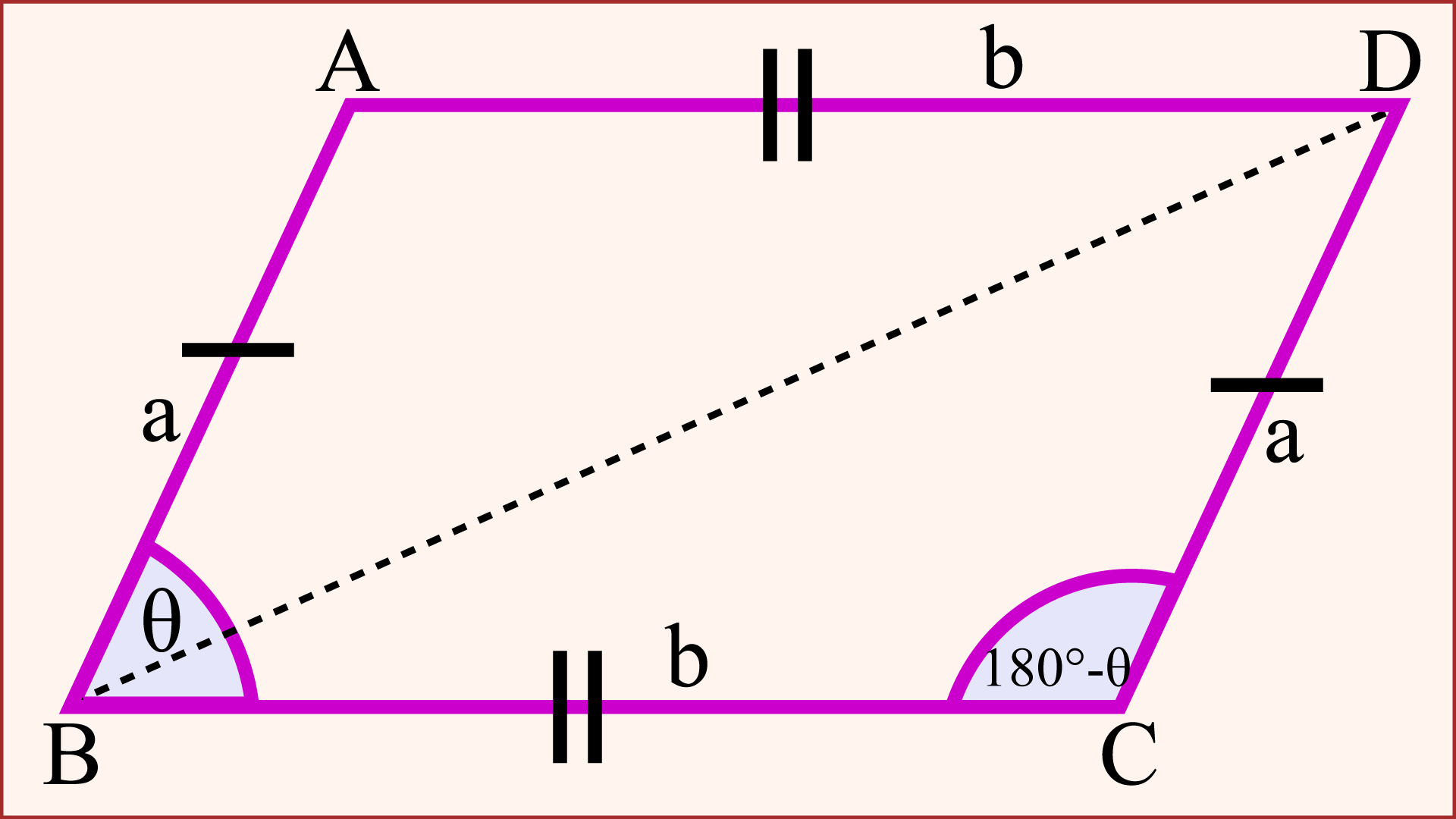
মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটি a ও b এবং তাদের অন্তর্ভূক্ত কোণ θ, যা একটি সূক্ষ্মকোণ। তাহলে, সামান্তরিকের কর্ণ নির্ণয়ের সূত্র ব্যবহার করে এর বৃহত্তম কর্ণ নির্ণয় করা যায়। আর সূত্রটি হবে
বৃহত্তম কর্ণ = √a2 + b2 + 2ab cosθ
লক্ষ করা যাচ্ছে, ক্ষূদ্রতম কোণের ক্ষেত্রে সূত্রের মাঝে - 2ab cosθ; কিন্তু বৃহত্তম কোণের ক্ষেত্রে সেখানে + 2ab cosθ হয়েছে। কেন ও কিভাবে এই পরিবর্তন হলো তা একটু খতিয়ে দেখা যাক।
উপরের প্রথম চিত্রে, ∠B = θ একটি সূক্ষ্মকোণ। কিন্তু ∠C = (180° - θ) একটি স্থূলকোণ। সুতরাং, প্রথম সূত্রে সূক্ষ্মকোণ, ∠B = θ এর স্থলে স্থূলকোণ ∠C = (180° - θ) বসালে কি পরিবর্তন হয় তা পরীক্ষা করি। অর্থাৎ, সামান্তরিকের কর্ণ নির্ণয়ের সূত্র √a2 + b2 - 2ab cosθ তে θ এর স্থলে স্থূলকোণ (180° - θ) বসালে সূত্রটি দাঁড়ায়,
√a2 + b2 - 2ab cos(180° - θ)
= √a2 + b2 - 2ab (- cosθ [ ∵ cos(180° - θ) = - cosθ ]
= √a2 + b2 + 2ab cosθ
উপরের দ্বিতীয় চিত্রে, ABCD একটি সামান্তরিক যার AB = CD = a এবং BC = AD = b। ∠B ও ∠D দুইটি সূক্ষ্মকোণ। এই কোণ দুইটির শীর্ষবিন্দু পরস্পর যোগ করলে বৃহত্তম কর্ণ BD উৎপন্ন হয়। আবার, a ও b বাহুদ্বয়ের অন্তর্গত কোণ ∠B = θ, যা একটি সূক্ষ্মকোণ কোণ। একারণে, ∠C = (180° - θ) একটি স্থূলকোণ। তাহলে, সামান্তরিকের কর্ণ নির্ণয়ের সূত্র ব্যবহার করে বৃহত্তম কর্ণটির দৈর্ঘ্য নির্ণয় করা যায় এবং সূত্রটি হবে,
বৃহত্তম কর্ণ BD = √a2 + b2 + 2ab cosθ
সামান্তরিকের সন্নিহিত বাহু দুইটি a ও b এবং তাদের অন্তর্ভূক্ত তাদের অন্তর্ভূক্ত কোণ θ একটি সূক্ষ্মকোণ হলে সামান্তরিকের বৃহত্তম কর্ণ নির্ণয়ের সূত্রটি হবে নিম্নরূপ:
বৃহত্তম কর্ণ = √a2 + b2 + 2ab cosθ
উদাহরণ: একটি সামান্তরিকের সন্নিহিত বাহুদ্বয় 18 সেন্টিমিটার ও 26 সেন্টিমিটারি এবং তাদের অন্তর্ভূক্ত কোণ 60° হলে সামান্তরিকটির কর্ণ দুইটির দৈর্ঘ্য কত?
সমাধান: সামান্তরিকের সন্নিহিত বাহু দুইটি a = 18 সেন্টিমিটার ও b = 26 সেন্টিমিটারি এবং তাদের অন্তর্ভূক্ত θ = 60°।
সামান্তরিকের কর্ণ নির্ণয়ের সূত্র অনুসারে,
ক্ষূদ্রতম কর্ণ = √a2 + b2 - 2ab cosθ
বা, ক্ষূদ্রতম কর্ণ = √182 + 262 - 2×18×26× cos60°
বা, ক্ষূদ্রতম কর্ণ = √324 + 676 - 2×18×26×0.5
বা, ক্ষূদ্রতম কর্ণ = √1000 - 468
বা, ক্ষূদ্রতম কর্ণ = √532
∴ ক্ষূদ্রতম কর্ণ ≈ 23.07
সুতরাং, ক্ষূদ্রতম কর্ণটির দৈর্ঘ্য 23.07 সেন্টিমিটার (প্রায়)।
আবার, সামান্তরিকের কর্ণ নির্ণয়ের সূত্র অনুসারে,
বৃহত্তম কর্ণ = √a2 + b2 + 2ab cosθ
বা, বৃহত্তম কর্ণ = √182 + 262 + 2×18×26× cos60°
বা, বৃহত্তম কর্ণ = √324 + 676 + 2×18×26×0.5
বা, বৃহত্তম কর্ণ = √1000 + 468
বা, বৃহত্তম কর্ণ = √1468
∴ বৃহত্তম কর্ণ ≈ 38.31
সুতরাং, বৃহত্তম কর্ণটির দৈর্ঘ্য 38.31 সেন্টিমিটার (প্রায়)।