আয়তক্ষেত্র কাকে বলে
এই টিউটোরিয়ালটি শেষে -
আয়তক্ষেত্র কাকে বলে - তা ব্যাখ্যা করতে পারা যাবে।
আয়তক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র বর্ণনা করতে পারা যাবে।
আয়তক্ষেত্রের কর্ণের সূত্র বিশ্লেষণ করতে পারা যাবে।
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র প্রয়োগ করতে পারা যাবে।
আয়তক্ষেত্র
যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল এবং কোণগুলো সমকোণ তাকে আয়তক্ষেত্র বলে।
অন্যভাবে বললে, যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান এবং প্রত্যেকটি কোণ সমকোণ তাকে আয়তক্ষেত্র বলে।
আয়তক্ষেত্রের সবচেয়ে সংক্ষিপ্ত সংজ্ঞা হলো - যে চতুর্ভুজের সবগুলো কোণ সমকোণ তাকে আয়তক্ষেত্র বলে। আবার বলা যায়, আয়ত দ্বারা আবদ্ধ ক্ষেত্রকে আয়তক্ষেত্র বলে।
তাহলে দেখা যাচ্ছে যে, আয়তক্ষেত্রের বিপরীত বাহুদ্বয় পরস্পর সমান। আবার, আয়তক্ষেত্রের প্রত্যেকটি কোণ এক-একটি সমকোণ বা ৯০০। তাছাড়া, আয়তক্ষেত্রের বিপরীত বাহুদ্বয় পরস্পর সমান হওয়ার কারণে বিপরীত বাহুগুলো পরস্পর সমান্তরালও বটে। আয়তক্ষেত্র হলো একটি বিশেষ ধরণের চতুর্ভুজ।

চিত্রে, ABCD একটি চতুর্ভুজ। AD ও BC পরস্পর বিপরীত বাহু ও তাদের দৈর্ঘ্য পরস্পর সমান এবং AD ও BC পরস্পর সমান্তরাল। অর্থাৎ, AD∥BC এবং AD = BC. আবার, AB ও CD পরস্পর বিপরীত বাহু ও তাদের দৈর্ঘ্য পরস্পর সমান এবং AB ও CD পরস্পর সমান্তরাল। অর্থাৎ, AB∥CD এবং AB = CD.
তাছাড়া, ABCD চতুর্ভুজের কোণগুলো সমকোণ বা ৯০°। অর্থাৎ,
∠ABC = এক সমকোণ বা ৯০°,
∠BCD = এক সমকোণ বা ৯০°,
∠ADC = এক সমকোণ বা ৯০° এবং
∠BAC = এক সমকোণ বা ৯০°।
লক্ষ্য করা যাচ্ছে যে, ABCD চতুর্ভুজটি আয়তক্ষেত্রের সকল বৈশিষ্ট্য ধারণ করে। অতএব, ABCD একটি আয়তক্ষেত্র।
আয়তক্ষেত্রের পরিসীমা
আয়তক্ষেত্রের বাহুগুলোর সমষ্টিকে আয়তক্ষেত্রের পরিসীমা বলে। অতএব, আয়তক্ষেত্রের চারটি বাহুর দৈর্ঘ্য পরস্পর যোগ করলে আয়তক্ষেত্রের পরিসীমা পাওয়া যায়।
আয়তক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র
আয়তক্ষেত্রের বিপরীত বাহুদ্বয় পরস্পর সমান। মনেকরি ABCD আয়তক্ষেত্রের দৈর্ঘ্য AB = CD = a এবং প্রস্থ BC = AD = b.
সুতরাং আয়তক্ষেত্রের পরিসীমার সূত্রটি হবে,
আয়তক্ষেত্রের পরিসীমা = (AB + BC + CD + AD) একক
বা, আয়তক্ষেত্রের পরিসীমা = (a + a+ b + b) একক
বা, আয়তক্ষেত্রের পরিসীমা = (2a + 2b) একক
∴ আয়তক্ষেত্রের পরিসীমা = 2×(a + b) একক
সুতরাং, আয়তক্ষেত্রের পরিসীমা =২×( দৈর্ঘ্য + প্রস্থ ) একক
আয়তক্ষেত্রের দৈর্ঘ্য a এবং প্রস্থ b হলে,
আয়তক্ষেত্রের পরিসীমা = 2×(a + b) একক।
আয়তক্ষেত্রের পরিসীমা =২×( দৈর্ঘ্য + প্রস্থ ) একক।
উদাহরণঃ
একটি আয়তক্ষেত্রের দৈর্ঘ্য ৫ সেমি ও প্রস্থ ৪ সেমি হলে আয়তক্ষেত্রের পরিসীমা কত হবে?
সমাধানঃ মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য a = ৫ সেমি এবং প্রস্থ b = ৪ সেমি।
আয়তক্ষেত্রের পরিসীমা = ২ ×(দৈর্ঘ্য + প্রস্থ) একক
বা, আয়তক্ষেত্রের পরিসীমা = ২ ×(a + b) একক
বা, আয়তক্ষেত্রের পরিসীমা = ২ ×(৫ + ৪) সেমি
বা, আয়তক্ষেত্রের পরিসীমা = (২ ×৯) সেমি
∴ আয়তক্ষেত্রের পরিসীমা = ১৮ সেমি।
আয়তক্ষেত্র উদাহরণ
আয়তক্ষেত্রের ক্ষেত্রফল
আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থের গুণফলকে আয়তক্ষেত্রের ক্ষেত্রফল বলে।
আয়তক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র
মনে করি, আয়তক্ষেত্রের দৈর্ঘ্য a একক, প্রস্থ b একক এবং ক্ষেত্রফল A বর্গ একক।
সুতরাং, আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক
∴ আয়তক্ষেত্রের ক্ষেত্রফল, A = ab বর্গ একক
আয়তক্ষেত্রের দৈর্ঘ্য a, প্রস্থ b এবং ক্ষেত্রফল A হলে,
আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক
আয়তক্ষেত্রের ক্ষেত্রফল, A = ab বর্গ একক
উদাহরণঃ
একটি আয়তক্ষেত্রের দৈর্ঘ্য ৪ সেমি ও প্রস্থ ৩ সেমি হলে আয়তক্ষেত্রটির ক্ষেত্রফল কত?
সমাধানঃ মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য a = ৪ সেমি ও প্রস্থ b = ৩ সেমি।
আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য × প্রস্থ) বর্গ একক
বা, আয়তক্ষেত্রের ক্ষেত্রফল = (a × b) বর্গ একক
বা, আয়তক্ষেত্রের ক্ষেত্রফল = (৪ × ৩) বর্গ সেমি
বা, আয়তক্ষেত্রের ক্ষেত্রফল = ১২ বর্গ সেমি
∴ আয়তক্ষেত্রের ক্ষেত্রফল = ১২ বর্গ সেমি।
আবার, সামান্তরিকের সাহায্যেও আয়তক্ষেত্র কাকে বলে - এ প্রশ্নের উত্তর দেওয়া যায়। অর্থাৎ, সামান্তরিকের সাহায্যেও আয়তক্ষেত্রকে সংজ্ঞায়িত করা যায়। সামান্তরিকের একটি কোণ সমকোণ হলে তাকে আয়তক্ষেত্র বলে। তাহলে, সামান্তরিক কিভাবে আয়তক্ষেত্র হয়? সামান্তরিকের একটি কোণ সমকোণ হলে অপর কোণগুলো আপনা-আপনি সমকোণ হয়ে যায়। তখন এটি আয়তক্ষেত্র আকার ধারণ করে। সুতরাং, আয়তক্ষেত্র হলো সামান্তরিকের একটি বিশেষ রূপ।
আয়তক্ষেত্রের কর্ণ
আয়তক্ষেত্রের দুইটি বিপরীত শীর্ষবিন্দু যোগ করলে যে রেখাংশ উৎপন্ন হয় তাকে আয়তক্ষেত্রের কর্ণ বলে। আয়তক্ষেত্রের এরূপ দুই জোড়া বিপরীত শীর্ষ বিন্দু সংযুক্ত করলে দুইটি কর্ণ পাওয়া যায়। আয়তক্ষেত্রের দুইটি কর্ণের দৈর্ঘ্য পরস্পর সমান। আবার, আয়তক্ষেত্রের কর্ণ দুইটি পরস্পরকে সমদ্বিখণ্ডিত করে।
আয়তক্ষেত্রের যেকোনো কর্ণ আয়তক্ষেত্রটিকে যে দুইটি ত্রিভুজে বিভক্ত করে তারা পরস্পর সর্বসম ত্রিভুজ। অধিকিন্তু, এই ত্রিভুজ দুইটির প্রত্যেকটি সমকোণী ত্রিভুজও বটে।
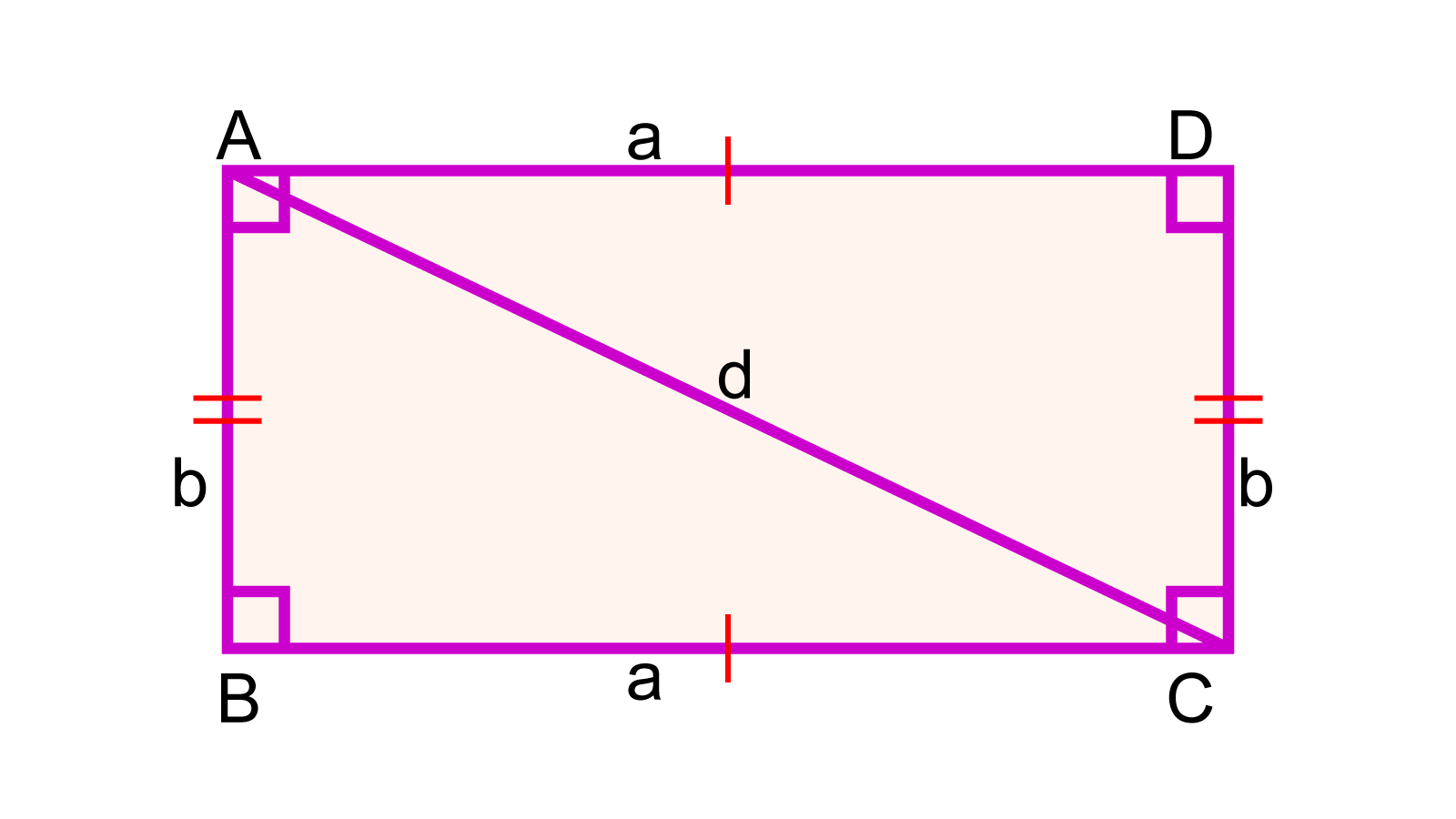
প্রমাণ: চিত্রে, ABCD আয়তক্ষেত্রের AC কর্ণ আয়তক্ষেত্রটিকে △ABC ও △ADC দুইটি ত্রিভুজে বিভক্ত করে।
এখন, △ABC ও △ADC - এ
AB = CD,
BC = AD এবং
AC = AC.
∴ △ABC ≅ △ADC
সুতরাং, △ABC ও △ADC পরস্পর সর্বসম ত্রিভুজ। (প্রমাণিত)।
আবার, △ABC -এ ∠ABC = এক সমকোণ বা ৯০°। অতএব, △ABC একটি সমকোণী ত্রিভুজ যার অতিভুজ AC.
তদ্রূপ, △ADC -এ ∠ADC = এক সমকোণ বা ৯০°। অতএব, △ADC একটি সমকোণী ত্রিভুজ যার অতিভুজ AC.
সুতরাং, △ABC ও △ADC ত্রিভুজ দুইটির প্রত্যেকটি সমকোণী ত্রিভুজ।
তাহলে, সমকোণী ত্রিভুজের সাহায্যেও আয়তক্ষেত্র কাকে বলে - এ প্রশ্নের উত্তর দেওয়া যায় অর্থাৎ, সমকোণী ত্রিভুজের সাহায্যে আয়তক্ষেত্রকে সংজ্ঞায়িত করলে দাঁড়ায়;
দুইটি সর্বসব সমকোণী ত্রিভুজকে অতিভুজ বরাবর যুক্ত করলে যে চতুর্ভুজ উৎপন্ন হয় তাকে আয়তক্ষেত্র বলে।
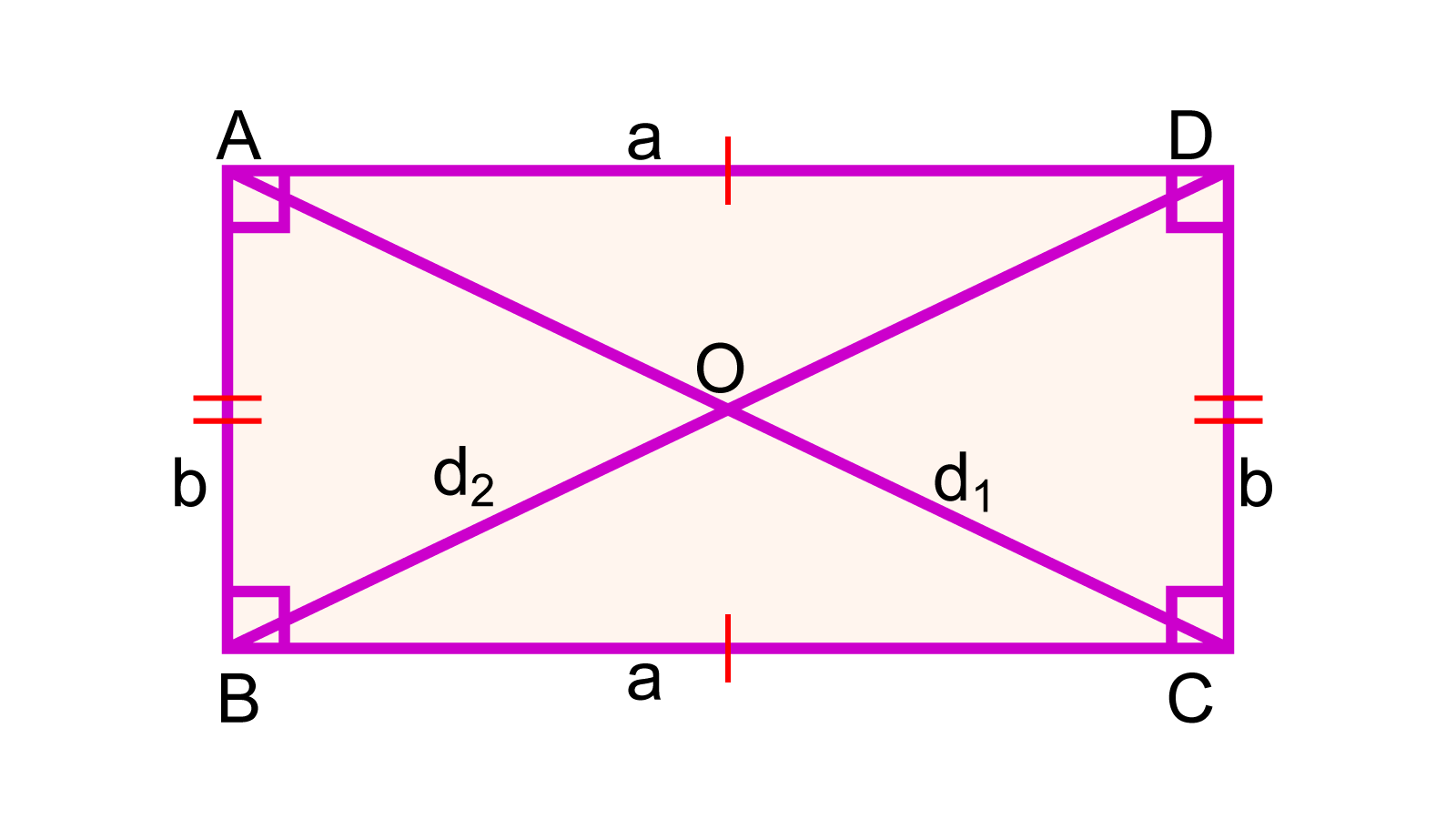
আয়তক্ষেত্রের কর্ণের সূত্র
মনেকরি, ABCD একটি আয়তক্ষেত্র যার দৈর্ঘ্য AD = BC = a এবং প্রস্থ AB = CD = b. আয়তক্ষেত্রটির একটি কর্ণ AC = d1 এবং অপর কর্ণ BD = d2.
তাহলে, সমকোণী ত্রিভুজ △ABC -এ
∠ABC = ৯০° এবং যার অতিভুজ d1.
পিথাগোরাসের উপপাদ্য অনুসারে,
AC2 = BC2 + AB2
বা, d12 = a2 + b2
∴ d1 = √(a2 + b2)
∴ কর্ণ = √(দৈর্ঘ্য)2 + (প্রস্থ)2 একক
আয়তক্ষেত্রের দৈর্ঘ্য a একক, প্রস্থ b একক এবং কর্ণ d একক হলে,
কর্ণ = √(দৈর্ঘ্য)2 + (প্রস্থ)2 একক
d = √(a2 + b2) একক
উদাহরণঃ
একটি আয়তক্ষেত্রের দৈর্ঘ্য ৩৫ সেমি ও প্রস্থ ১২ সেমি হলে আয়তক্ষেত্রের কর্ণ কত?
সমাধানঃ মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য a = ৩৫ সেমি এবং প্রস্থ b = ১২ সেমি।
এখন আয়তক্ষেত্রের কর্ণ নির্ণয়ের সূত্র ব্যবহার করে পাওয়া যায়,
আয়তক্ষেত্রের কর্ণ = √(দৈর্ঘ্য)2 + (প্রস্থ)2 একক
বা, আয়তক্ষেত্রের কর্ণ = √a2 + b2 একক
বা, আয়তক্ষেত্রের কর্ণ = √(৩৫)২ + (১২)২ সেমি
বা, আয়তক্ষেত্রের কর্ণ = √১২২৫ + ১৪৪ সেমি
বা, আয়তক্ষেত্রের কর্ণ = √১৩৬৯ সেমি
বা, আয়তক্ষেত্রের কর্ণ = √(৩৭)২ সেমি
বা, আয়তক্ষেত্রের কর্ণ = ৩৭ সেমি
∴ আয়তক্ষেত্রের কর্ণ = ৩৭ সেমি
আয়তক্ষেত্রের উপর বিভিন্ন প্রতিযোগিতামূলক পরীক্ষায় আসা কয়েকটি প্রশ্ন
প্রশ্ন ১: কোনো বর্গক্ষেত্রের বাহুর দৈর্ঘ্য ২০% বৃদ্ধি পেলে তার ক্ষেত্রফল শতকরা কত বৃদ্ধি পায়?
ক. ২০%
খ. ৩০%
গ. ৩৮%
ঘ. ৪৪%
উত্তর: ৪৪%
প্রশ্ন ২: একটি আয়তাকার মাঠের ক্ষেত্রফল ১০০০ বর্গমিটার। মাঠের দৈর্ঘ্য ৪০ মিটার হলে মাঠের পরিসীমা কত? (ব্যাংক নিয়োগ)
ক. ১২০ মিটার
খ. ১৩০ মিটার
গ. ১৩২ মিটার
ঘ. ১৩৫ মিটার
উত্তর: ১৩০ মিটার
প্রশ্ন ৩: একটি আয়তাকার বাড়ির পরিসীমা ৪৪ গজ এবং ঘরের দৈর্ঘ্য ৩৬ ফুট। ঘরের প্রস্থ কত গজ? (ব্যাংক নিয়োগ)
ক. ১০ গজ
খ. ৮ গজ
গ. ১২ গজ
ঘ. ৯ গজ
উত্তর: ১০ গজ
প্রশ্ন ৪: একটি আয়তাকার ক্ষেত্রের দৈর্ঘ্য বিস্তারের ৩ গুণ। দৈর্ঘ্য ৪৮ মিটার হলে, এর পরিসীমা কত? (শি. নি.)
ক. ১২৮ মিটার
খ. ১৩০ মিটার
গ. ১৫৬ মিটার
ঘ. ১৫০ মিটার
উত্তর: ১২৮ মিটার
প্রশ্ন ৫: একটি আয়তক্ষেত্রের দৈর্ঘ্য প্রস্থের ২ গুণ। আয়তক্ষেত্রটির ক্ষেত্রফল ১২৫০ বর্গমিটার, এর দৈর্ঘ্য কত? (৩০তম বিসিএস)
ক. ৪০ মিটার
খ. ৫০ মিটার
গ. ৬০ মিটার
ঘ. ৫৫ মিটার
উত্তর: ৫০ মিটার
প্রশ্ন ৬: একটি আয়তাকার জমির ক্ষেত্রফল ২৪ এয়র। দৈর্ঘ্য ও প্রস্থের অনুাপাত ৩:২ হলে ঐ জমির পরিসীমা কত? (স.চা.)
ক. ১৫০ মিটার
খ. ২৫০ মিটার
গ. ২০০ মিটার
ঘ. ৩০০ মিটার
উত্তর: ২০০ মিটার
প্রশ্ন ৭: কোন ক্ষেত্রগুলোর কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে? (স.চা.)
ক. রম্বস ও বর্গক্ষেত্র
খ. আয়তক্ষেত্র ও বর্গক্ষেত্র
গ. রম্বস ও সামান্তরিক
ঘ. সামান্তরকি ও ট্রাপিজিয়াম
উত্তর: রম্বস ও বর্গক্ষেত্র
সচরাচর যেসব প্রশ্ন করা হয়ে থাকে - Frequently Asked Questions (FAQ)
আয়তক্ষেত্র কাকে বলে - এ সংক্রান্ত সচরাচর যেসব প্রশ্নসমূহ মানুষ করে থাকে।
উত্তরঃ যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল এবং প্রত্যেকটি অন্তঃস্থ কোণ সমকোণ বা ৯০° হলে তাকে আয়ত বলে। আয়তের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল। আবার, এর বিপরীত কোণগুলোও পরস্পর সমান এবং প্রত্যেকটি কোণের পরিমাপ ৯০°।
উত্তরঃ আয়তক্ষেত্র বিশ্লেষণ করলে কতকগুলো আয়তক্ষেত্রের বৈশিষ্ট্য পরিলক্ষিত হয়। আয়তের তিনটি বৈশিষ্ট্য নিচে দেওয়া হলো।
- আয়তক্ষেত্রের বাহুগুলো পরস্পর সমান ও সমান্তরাল।
- আয়তক্ষেত্রের কর্ণ দুইটির দৈর্ঘ্য পরস্পর সমান।
- আয়তক্ষেত্রের প্রত্যেকটি কোণের পরিমাপ সমকোণ বা ৯০°।
উত্তরঃ আয়তক্ষেত্রের চারটি বাহুর সমষ্টিকে আয়তক্ষেত্রের পরিসীমা বা আয়তক্ষেত্রের পরিধি বলে। আয়তক্ষেত্রের বিপরীত বাহু দুইটির দৈর্ঘ্য পরস্পর সমান।
সুতরাং, আয়তক্ষেত্রের পরিধি নির্ণয়ের সূত্র হবে নিম্নরূপ:
আয়তক্ষেত্রের পরিধি বা পরিসীমা = ২×( দৈর্ঘ্য + প্রস্থ ) একক।
উত্তরঃ আয়তক্ষেত্রের যেকোনো দুইটি বিপরীত কৌণিক বিন্দু যোগ করলে যে রেখাংশ পাওয়া যায় তাকে আয়তক্ষেত্রের কর্ণ বলে। আয়তক্ষেত্রের সর্বোচ্চ দুইটি কর্ণ আঁকা যায়। আয়তক্ষেত্রের কর্ণদ্বয় পরস্পর সমান।
আয়তক্ষেত্রের কর্ণের সূত্র = √(দৈর্ঘ্য)2 + (প্রস্থ)2 একক
উত্তরঃ আয়তক্ষেত্রের দৈর্ঘ্যকে প্রস্থ দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়। সুতরাং, আয়তক্ষেত্রের ক্ষেত্রফলের সূত্র হবে নিম্নরূপ:
আয়তক্ষেত্রের ক্ষেত্রফল= (দৈর্ঘ্য × প্রস্থ) বর্গ একক।