ত্রিভুজের ক্ষেত্রফলের সূত্র
এই টিউটোরিয়ালটি শেষে -
ত্রিভুজের ক্ষেত্রফলের সূত্র বর্ণনা করতে পারা যাবে।
সর্বপ্রকার ত্রিভুজের ক্ষেত্রফলের সূত্রের তালিকা তৈরি করতে পারা যাবে।
সূত্র প্রয়োগ করে সব ধরণের ত্রিভুজের ক্ষেত্রফল নির্ণয় করতে পারা যাবে।
ত্রিভুজের ক্ষেত্রফলের সূত্র
যেসব সূত্র ব্যবহার করে ত্রিভুজের ক্ষেত্রফল নির্ণয় করা হয় সেগুলোই ত্রিভুজের ক্ষেত্রফলের সূত্র বলে পরিচিত। দ্বিমাত্রিক জ্যামিতিতে বেশ কয়েক ধরণের ত্রিভুজ বিরাজমান। ভিন্ন ভিন্ন ত্রিভুজের ক্ষেত্রফলের সূত্র প্রয়োগ করে ভিন্ন ভিন্ন ত্রিভুজের ক্ষেত্রফল নির্ণয় করা হয়।

ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র আলোচনার পূর্বে ত্রিভুজের ক্ষেত্রফল কি তা জানা প্রয়োজন। তিনটি রেখাংশ দ্বারা আবদ্ধ ক্ষেত্রকে ত্রিভুজক্ষেত্র বলে। আর এই রেখাংশ তিনটি দ্বারা যখন ত্রিভুজ গঠিত হয়, প্রত্যেকটি রেখাংশকে ত্রিভুজের এক-একটি বাহু বলে। তাই বলা হয়, তিনটি বাহু দ্বারা গঠিত ক্ষেত্রকে ত্রিভুজক্ষেত্র বলে।
ত্রিভুজের ভূমি ও উচ্চতার গুণফলকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়। তাহলে কোনো ত্রিভুজের ভূমি ও উচ্চতা জানা থাকলে ত্রিভুজের ক্ষেত্রফল নির্ণয় করা যায়।
∴ ত্রিভুজের ক্ষেত্রফলের সূত্র = 12 × (ভূমি × উচ্চতা) বর্গ একক
ত্রিভুজের ক্ষেত্রফলের সূত্র = 12 × (ভূমি × উচ্চতা) বর্গ একক
সমতল জ্যামিতিতে বেশ কয়েক ধরণের ত্রিভুজ রয়েছে। তবে ভিন্ন ভিন্ন ত্রিভুজের ক্ষেত্রফল নির্ণয় করার জন্য ভিন্ন সূত্র জানার প্রয়োজন হয় না। যে কয় ধরণের ত্রিভুজের ক্ষেত্রফলের সূত্র জানা থাকলে অন্যান্য সকল ত্রিভুজের ক্ষেত্রফল নির্ণয় করা যায় তার একটি তালিকা নিচে দেওয়া হলো।
- বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
- সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
- সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
- সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র
- সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
বিষমবাহু ত্রিভুজের বাহু তিনটি পরস্পর অসমান। বিষমবাহু ত্রিভুজ অন্যান্য সকল ত্রিভুজকে প্রতিনিধিত্ব করে। তাই এই ত্রিভুজের ক্ষেত্রফলের সূত্র প্রয়োগ করে অন্যান্য সকল ত্রিভুজের ক্ষেত্রফল নির্ণয় করা যায়।

মনেকরি, ABC একটি বিষমবাহু ত্রিভুজ যার বাহু তিনটির দৈর্ঘ্য যথাক্রমে a একক, b একক, c একক; অর্ধ-পরিসীমা s একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে, বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র,
A =√s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2.
বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a একক, b একক, c একক; অর্ধ-পরিসীমা s একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A =√s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2.
সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয়ের আগে সমদ্বিবাহু ত্রিভুজের বাহুর বৈশিষ্ট্য জানা জরুরী। সমদ্বিবাহু ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য পরস্পর সমান। এটি একটি বিশেষ ত্রিভুজ। এই ত্রিভুজের শীর্ষ বিন্দু থেকে ভূমির উপর লম্ব অঙ্কন করলে তা ভূমিকে সমদ্বিখণ্ডিত করে। তাই সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করার সময় ভূমি সম্পর্কে জ্ঞান থাকা আবশ্যক।

মনেকরি, △ABC একটি সমদ্বিবাহু ত্রিভুজ যার সমান সমান বাহুর দৈর্ঘ্য a একক, ভূমির দৈর্ঘ্য b একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র,
A = b4 √4a2 - b2 বর্গ একক।
সমদ্বিবাহু ত্রিভুজের সমান বাহুর দৈর্ঘ্য a একক, ভূমির দৈর্ঘ্য b একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = b4 √4a2 - b2 বর্গ একক।
সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
সমবাহু ত্রিভুজের বাহু তিনটির দৈর্ঘ্য পরস্পর সমান। বাহুভেদে সমবাহু ত্রিভুজ একটি সুষম ত্রিভুজ।

একারণে বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র থেকে খুব সহজে সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র প্রতিপাদন করা যায়। বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a, b ও c একক হলে এবং সবগুলো বাহুর স্থলে a বসালে সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র প্রতিপাদিত হয়। তাছাড়া, সমবাহু ত্রিভুজ একটি সুষম বহুভুজ যার প্রত্যেকটি কোণের পরিমাপ ৬০°। এ কারণে সুষম বহুভুজের ক্ষেত্রফলের সূত্র থেকেও সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র সহজে নির্ণয় করা যায়।
মনেকরি, △ABC একটি সমবাহু ত্রিভুজ যার প্রত্যেকটি বাহুর দৈর্ঘ্য a একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র, A = √34 a2 বর্গ একক।
সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = √34 a2 বর্গ একক।
সূক্ষ্মকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র
শুধু কোণের উপর নির্ভর করে কোনো ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করা যায় না। যেকোনো ত্রিভুজের ক্ষেত্রফল নির্ণয় করতে হলে তার বাহুর দৈর্ঘ্য জানা থাকতে হয়। একারণে সূক্ষ্মকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করার জন্য সেটি বাহুভেদে কোন ধরণের সূক্ষ্মকোণী ত্রিভুজ তা নির্ণয় করতে হয়। বাহুভেদে সূক্ষ্মকোণী ত্রিভুজ বেশ কয়েক ধরণের হতে পারে। যেমন - বিষমবাহু সূক্ষ্মকোণী ত্রিভুজ, সমদ্বিবাহু সূক্ষ্মকোণী ত্রিভুজ, সমবাহু সূক্ষ্মকোণী ত্রিভুজ ইত্যাদি। আবার সব বিষমবাহু ত্রিভুজই সূক্ষ্মকোণী ত্রিভুজ নয়। কারণ বিষমবাহু ত্রিভুজটি স্থূলকোণী বিষমবাহু ত্রিভুজ হতে পারে বা সমকোণী বিষমবাহু ত্রিভুজও হতে পারে।
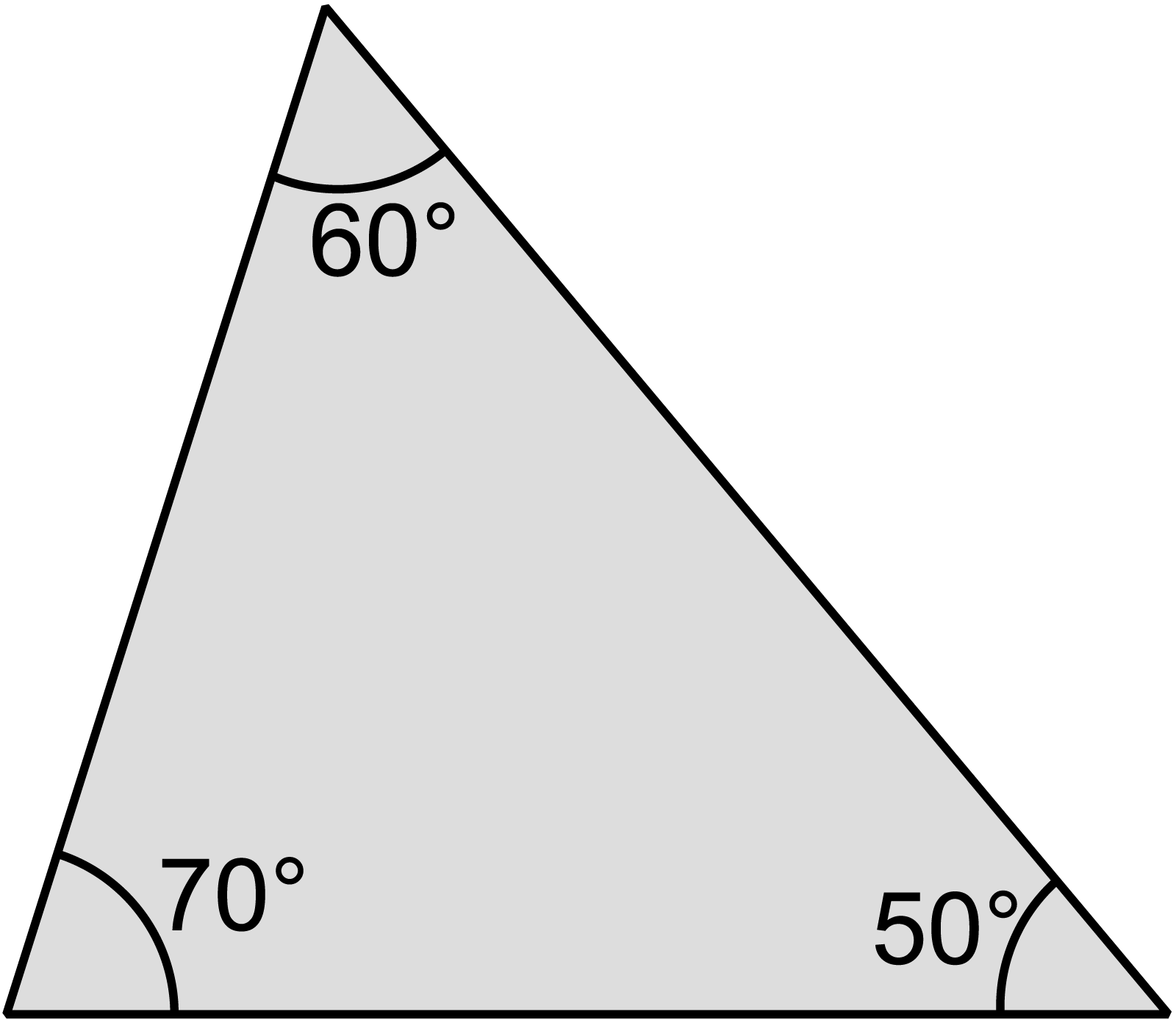
অতএব, যেকোনো সূক্ষ্মকোণী ত্রিভুজের ক্ষেত্রফল নির্ণয় করতে বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র ব্যবহার করা হয়।
মনেকরি, ABC একটি সূক্ষ্মকোণী ত্রিভুজ যার বাহুগুলোর দৈর্ঘ্য a একক, b একক, c একক; পরিসীমার অর্ধেক s একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে, সূক্ষ্মকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র,
A = √s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2.
যেকোনো সূক্ষ্মকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a একক, b একক, c একক; পরিসীমার অর্ধেক s একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = √s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2.
স্থূলকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র

আগেই বলা হয়েছে, শুধু কোণের ভিত্তিতে কোনো ত্রিভুজের ক্ষেত্রফল নির্ণয় করা যায় না। তাই বাহুর দৈর্ঘ্য না জানা থাকলে ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করা যায় না। এজন্য স্থূলকোণী ত্রিভুজের ক্ষেত্রফল নির্ণয় করতে বিষমবাহু স্থূলকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র প্রয়োগ করা হয়। মনেকরি, ABC একটি স্থূলকোণী ত্রিভুজ যার বাহুত্রয় a, b, c একক, অর্ধপরিসীমা s একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে স্থূলকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র,
A = √s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2.
স্থূলকোণী ত্রিভুজের বাহুত্রয় a একক, b একক, c একক; অর্ধ-পরিসীমা s একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = √s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2.
সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র
সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করতে ত্রিভুজটির ভূমি ও লম্ব জানা থাকতে হয়। অর্থাৎ, সমকোণী ত্রিভুজের ভূমি ও লম্বের উপর উপর নির্ভর করে সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করা হয়। সমকোণী ত্রিভুজের একটি কোণ ৯০° বা সমকোণ হওয়ার কারণে ভূমি ও লম্ব পরস্পর লম্ব। সমকোণী ত্রিভূজের লম্ব ও ভূমির দৈর্ঘ্যের গুণফলকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়।
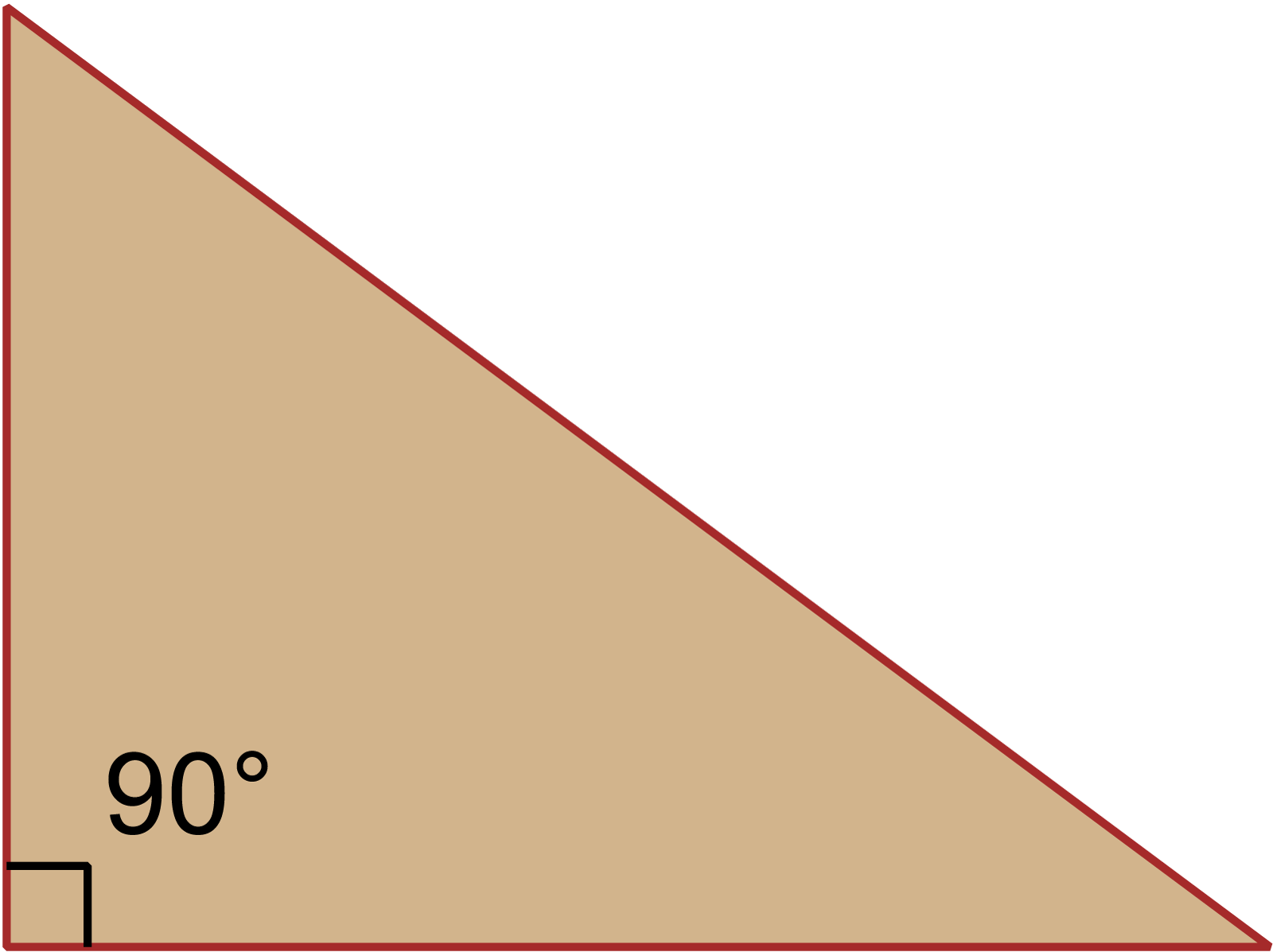
মনেকরি, △ABC একটি সমকোণী ত্রিভুজ যার লম্বের দৈর্ঘ্য a একক, ভূমির দৈর্ঘ্য b একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে, সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র,
A = 12 ab বর্গ একক।
সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য b একক, লম্বের দৈর্ঘ্য a একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = 12 ab বর্গ একক।
সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র
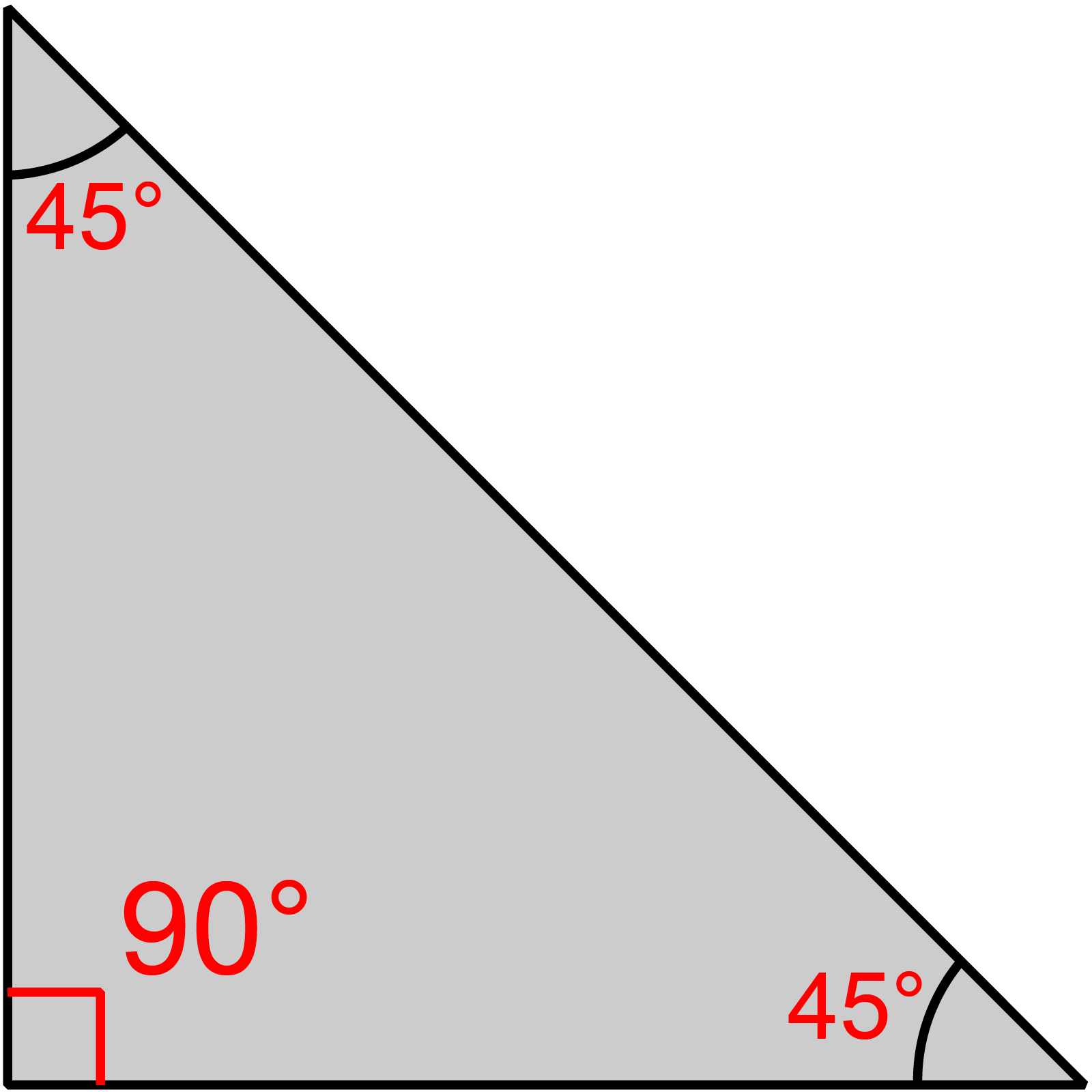
সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করার আগে বাহু ও কোণভেদে এই ত্রিভুজটি একটু বিশ্লেষণ করলে বিষয়টি সহজতর হয়। সমদ্বিবাহু সমকোণী ত্রিভুজের একটি কোণ সমকোণ। আবার এই ত্রিভুজটি একটি সমদ্বিাবাহু ত্রিভুজ। তাই সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্রে বাহুদ্বয় সমান কথাটি প্রয়োগ করলে সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র পাওয়া যাবে।
মনেকরি, △ABC একটি সমকোণী ত্রিভুজ যার লম্বের দৈর্ঘ্য a একক, ভূমির দৈর্ঘ্য b একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে, সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র,
A = 12 ab বর্গ একক।
এখন, বাহু a = b হলে, A = 12 aa বর্গ একক অর্থাৎ, A = 12 a2 বর্গ একক।
সমকোণী সমদ্বিবাহু ত্রিভুজের সমান সমান বাহুর দৈর্ঘ্য a একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = 12 a2।
বাহুদ্বয়ের অন্তর্ভূক্ত কোণ ত্রিভুজের ক্ষেত্রফলের সূত্র
যেকোনো ত্রিভুজের যেকোনো দুইটি বাহু ও তাদের অন্তর্ভূক্ত কোণ দেওয়া থাকলে ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করা যায়। কোনো ত্রিভুজের দুইটি বাহু ও তাদের অন্তর্ভূক্ত কোণের sine এর গুণফলের অর্ধেক হলো ঐ ত্রিভুজের ক্ষেত্রফল।
∴ ত্রিভুজের ক্ষেত্রফলের সূত্র = 12 × (১ম বাহু × ২য় বাহু × sinθ) বর্গ একক।
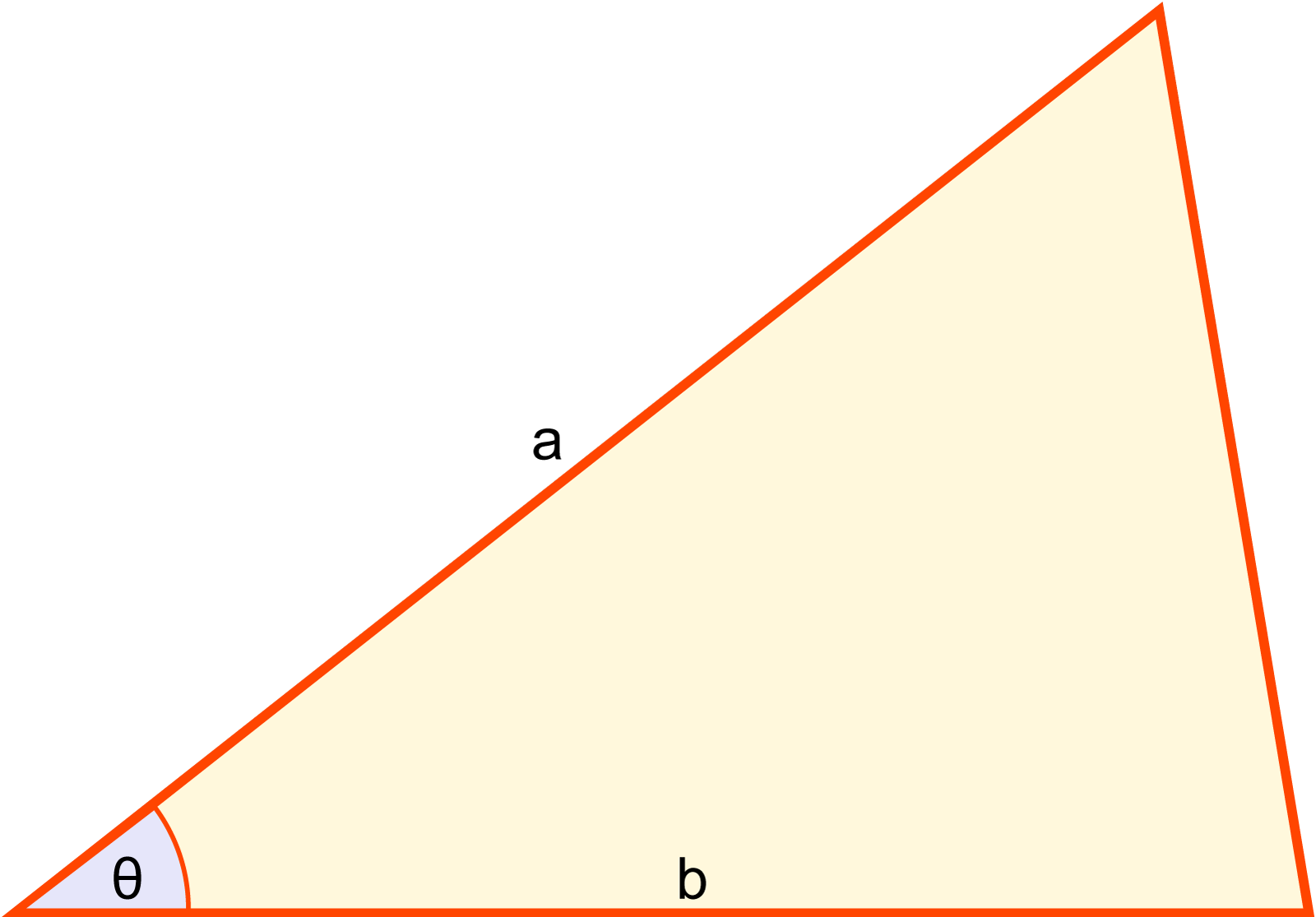
মনেকরি, ABC ত্রিভুজের যেকোনো দুইটি বাহু a ও b; তাদের অন্তর্ভূক্ত কোণ θ এবং ক্ষেত্রফল A বর্গ একক। তাহলে,
ত্রিভুজের ক্ষেত্রফলের সূত্র, A = 12 absinθ বর্গ একক।
ত্রিভুজের যেকোনো দুইটি বাহুর দৈর্ঘ্য a ও b; তাদের অন্তর্ভূক্ত কোণ θ এবং ক্ষেত্রফল A বর্গ একক হলে,
A = 12 absinθ বর্গ একক।
ত্রিভুজের সূত্রাবলী
ত্রিভুজের সূত্র ব্যবহার করে ত্রিভুজের ক্ষেত্রফল নির্ণয় করা হয়। ত্রিভুজের ক্ষেত্রফল নির্ণয় করার জন্য সচরাচর যেসব ত্রিভুজের সূত্রাবলী ব্যবহার করা হয় তার একটি তালিকা নিচে দেওয়া হলো।
| ত্রিভুজের নাম | বাহু | ত্রিভুজের ক্ষেত্রফলের সূত্র |
|---|---|---|
| যেকোনো ত্রিভুজ | ভূমি, উচ্চতা | 12 × (ভূমি × উচ্চতা) বর্গ একক |
| বিষমবাহু ত্রিভুজ | a, b, c | √s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2 |
| সমদ্বিবাহু ত্রিভুজ | সমান বাহু a, ভূমি b | b4 √4a2 - b2 বর্গ একক |
| সমবাহু ত্রিভুজ | a | √34 a2 বর্গ একক |
| সূক্ষ্মকোণী ত্রিভুজ | a, b, c | √s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2 |
| স্থূলকোণী ত্রিভুজ | a, b, c | √s(s - a)(s - b)(s - c) বর্গ একক; যেখানে s = a + b + c2 |
| সমকোণী ত্রিভুজ | সমকোণ সংলগ্ন বাহু a ও b | 12 ab বর্গ একক |
| সমকোণী সমদ্বিবাহু ত্রিভুজ | সমকোণ সংলগ্ন বাহু a | 12 a2 বর্গ একক |
| যেকোনো ত্রিভুজ | বাহু a,b; অন্তর্ভূক্ত ∠θ | 12 absinθ বর্গ একক |