ত্রিভুজের পরিসীমা ও ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র
এই টিউটোরিয়ালটি শেষে -
ত্রিভুজের পরিসীমা বর্ণনা করতে পারা যাবে।
ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র প্রতিপাদন করতে পারা যাবে।
সর্বপ্রকার ত্রিভুজের পরিসীমার সূত্র এবং তাদের তালিকা তৈরি করতে পারা যাবে।
ত্রিভুজের পরিসীমা সূত্র প্রয়োগ করে ত্রিভুজের পরিসীমা নির্ণয় করতে পারা যাবে।
ত্রিভুজের পরিসীমা কাকে বলে
ত্রিভুজের তিন বাহুর দৈর্ঘ্যের সমষ্টিকে ত্রিভুজের পরিসীমা বলে। তাহলে ত্রিভুজের পরিসীমা হলো ত্রিভুজের বহিঃসীমানার দৈর্ঘ্য। উদাহরণস্বরূপ - একটি ত্রিভুজের তিন বাহুর দৈর্ঘ্য ৪ সে.মি., ৫ সে.মি. ও ৬ সে.মি. হলে তার পরিসীমা হবে (৪ + ৫ + ৬) সে.মি. বা ১৫ সে.মি.।

দৈনন্দিন জীবনে ত্রিভুজের পরিসীমা পদ্ধতির খুবই প্রয়োগ দেখা যায়। যেমন - একটি ত্রিভুজ আকৃতি বাগানের পরিসীমা নির্ণয় করে এর চারদিকে বেড়া বা প্রাচীর দিতে কত টাকা খরচ হবে তা বেড়া দেওয়ার আগেই নিখুঁতভাবে হিসাব করা যায়।
ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র
ত্রিভুজের পরিসীমা হলো ত্রিভুজের বাহুগুলোর সমষ্টি। মনেকরি, ABC একটি ত্রিভুজ যার বাহু তিনটির পরিমাপ a একক, b একক, c একক এবং পরিসীমা P একক। তাহলে ত্রিভুজের পরিসীমার সূত্র হবে,
P = (a + b + c) একক।
একটি ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a একক, b একক, c একক এবং পরিসীমা P একক হলে,
P = (a + b + c) একক।
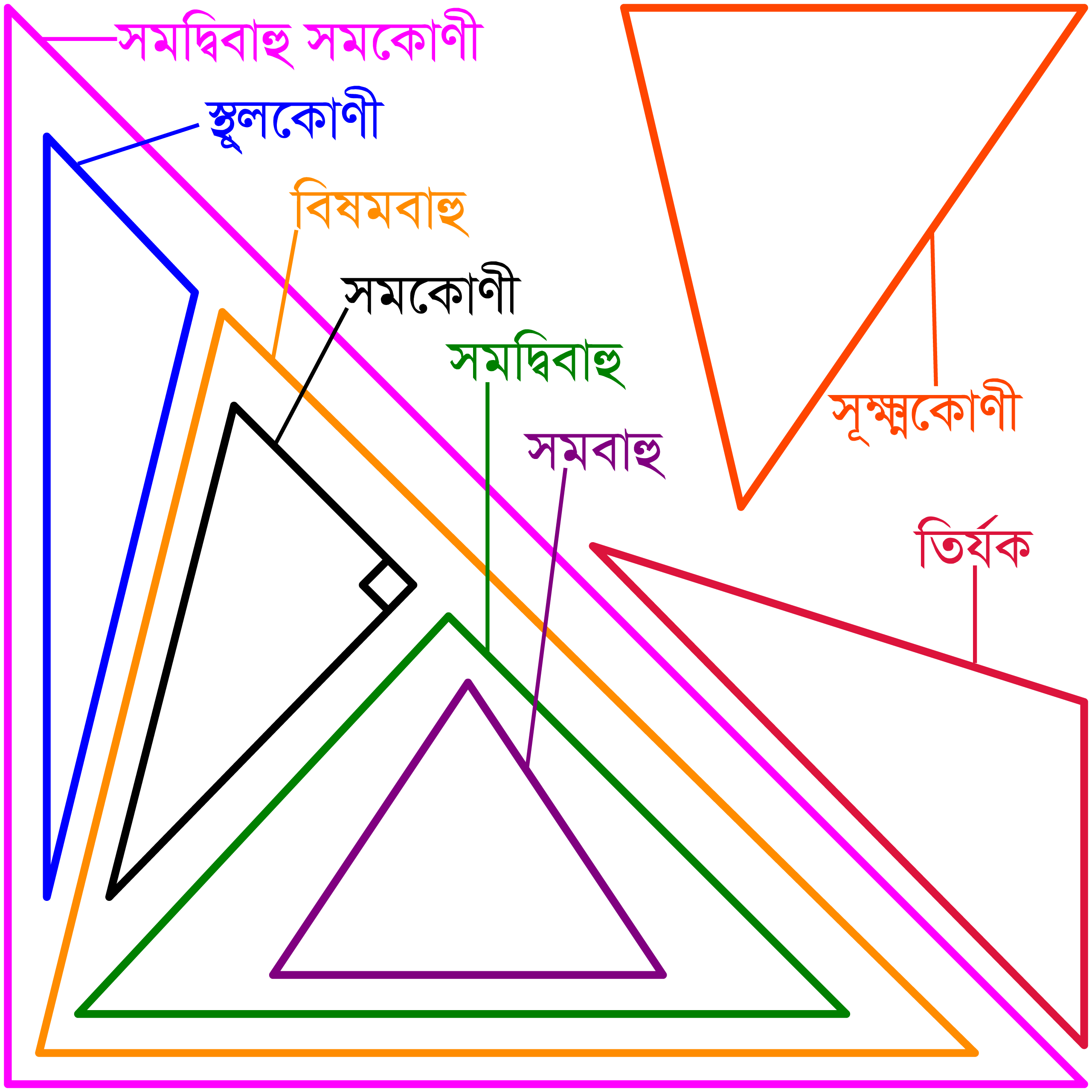
সমতল জ্যামিতিতে কয়েক ধরণের ত্রিভুজ বিরাজমান। কিন্তু ভিন্ন ভিন্ন ত্রিভুজের পরিসীমা নির্ণয় করার জন্য ভিন্ন ভিন্ন সূত্র ব্যবহার করার প্রয়োজন হয় না। যেসব ত্রিভুজের পরসীমার সূত্র জানা থাকলে অন্যান্য সকল ত্রিভুজের পরিসীমা নির্ণয় করা যায় তাদের একটি তালিকা নিচে প্রকাশ করা হলো।
- বিষমবাহু ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র
- সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র
- সমবাহু ত্রিভুজের পরিসীমার সূত্র
- সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র
- সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র
উদাহরণঃ একটি মাঠে একটি খুঁটি স্থাপন করা হলো। প্রথম খুঁটি থেকে ২২ মিটার দূরে দ্বিতীয় আরেকটি খুঁটি স্থাপন করা হলো। তৃতীয় খুঁটিটি এমনভাবে স্থাপন করা হলো যেন তা দ্বিতীয় খুঁটি হতে ২৭ মিটার দূরত্বে এবং প্রথম খুঁটি হতে ৩৩ মিটার দূরত্বে অবস্থিত হয়। খুঁটি তিনটি দ্বারা আবদ্ধ ভূমির পরিসীমা কত?
সমাধানঃ খুঁটি তিনটি দ্বারা আবদ্ধ ভূমি একটি ত্রিভুজাকৃতি ভূমি। সুতরাং, এটি একটি ত্রিভুজের পরিসীমা বিষয়ক সমস্যা।
মনেকরি,
১ম খুঁটি থেকে ২য় খুঁটির দূরত্ব a = ২২ মিটার,
২য় খুঁটি থেকে ৩য় খুঁটির দূরত্ব b = ২৭ মিটার এবং
১ম খুঁটি থেকে ৩য় খুঁটির দূরত্ব c = ৩৩ মিটার
খুঁটি তিনটি দ্বারা আবদ্ধ ভূমির পরিসীমা P হলে,
P = (a + b + c) একক
বা, P = (২২ + ২৭ + ৩৩) মিটার
∴ P = ৮২ মিটার
∴ খুঁটি তিনটি দ্বারা আবদ্ধ ত্রিভুজাকৃতি ভূমির পরিসীমা ৮২ মিটার।
বিষমবাহু ত্রিভুজের পরিসীমা
বিষমবাহু ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের সমষ্টিকে বিষমবাহু ত্রিভুজের পরিসীমা বলে। বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য পরস্পর অসমান। বিষমবাহু ত্রিভুজ সকল ত্রিভুজের সাধারণ রূপ। একারণে বিষমবাহু ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র ব্যবহার করে সর্বপ্রকার ত্রিভুজের পরিসীমা নির্ণয় করা যায়।

মনেকরি, △ABC একটি বিষমবাহু ত্রিভুজ। যদি ত্রিভুজটির বাহু তিনটির পরিমাপ যথাক্রমে a একক, b একক, c একক এবং পরিসীমা P একক হয়, তাহলে বিষমবাহু ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র,
P = (a + b + c) একক।
বিষমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a একক, b একক, c একক এবং পরিসীমা P একক হলে,
P = (a + b + c) একক।
সমদ্বিবাহু ত্রিভুজের পরিসীমা
সমদ্বিবাহু ত্রিভুজের অসমান বাহু ও সমান সমান বাহুর দ্বিগুণের সমষ্টিকে সমদ্বিবাহু ত্রিভুজের পরিসীমা বলে। যেহেতু ত্রিভুজের পরিসীমা হলো বাহু তিনটির যোগফল এবং সমদ্বিবাহু ত্রিভুজের দুইটি বাহু পরস্পর সমান, সেকারণে সমান বাহুর দৈর্ঘ্যকে দ্বিগুণ করে অসমান বাহুর সাথে যোগ করা হয়।
মনেকরি, △ABC সমদ্বিবাহু ত্রিভুজ যার অসমান বাহুর পরিমাপ b একক এবং সমান সমান বাহুর পরিমাপ a একক। তাহলে সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র হবে,
P = (2a + b) একক।

একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুর দৈর্ঘ্য a একক, অসমান বাহুর দৈর্ঘ্য b একক এবং পরিসীমা P একক হলে,
P = (2a + b) একক।
সমবাহু ত্রিভুজের পরিসীমা
সমবাহু ত্রিভুজের এক বাহুর দৈর্ঘ্যের তিনগুণকে সমবাহু ত্রিভুজের পরিসীমা বলে। সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য সমান। একারণে সমবাহু ত্রিভুজের পরিসীমা হলো তিনটি বাহুর সমষ্টি বা এক বাহুর তিনগুণ। সমবাহু ত্রিভুজ মূলতঃ একটি সুষম ত্রিভুজ।
সমবাহু ত্রিভুজের একটি বাহু a একক হলে পরিসীমা = 3a একক।

বিষমবাহু ত্রিভুজের পরিসীমার সূত্র (a + b + c) একক যেখানে a = b = c বসালে পরিসীমা (a + a + a) একক বা 3a একক হয়।
আবার, সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র (2a + b) একক যেখানে a = b বসালে পরিসীমা (2a + a) একক বা 3a একক হয়।
মনেকরি, △ABC একটি সমবাহু ত্রিভুজ যার একটি বাহুর দৈর্ঘ্য a একক। তাহলে সমবাহু ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র,
P = 3a একক।
সমবাহু ত্রিভুজের প্রত্যেক বাহুর দৈর্ঘ্য a একক এবং পরিসীমা P একক হলে,
P = 3a একক।
সমকোণী ত্রিভুজের পরিসীমা
সমকোণী ত্রিভুজের লম্ব, ভূমি ও অতিভূজের সমষ্টিকে সমকোণী ত্রিভুজের পরিসীমা বলে। অন্যভাবে বললে, সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহুদ্বয় ও অতিভূজের সমষ্টিকে সমকোণী ত্রিভুজের পরিসীমা বলে। অতএব, সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র = (লম্ব + ভূমি + অতিভূজ) একক।
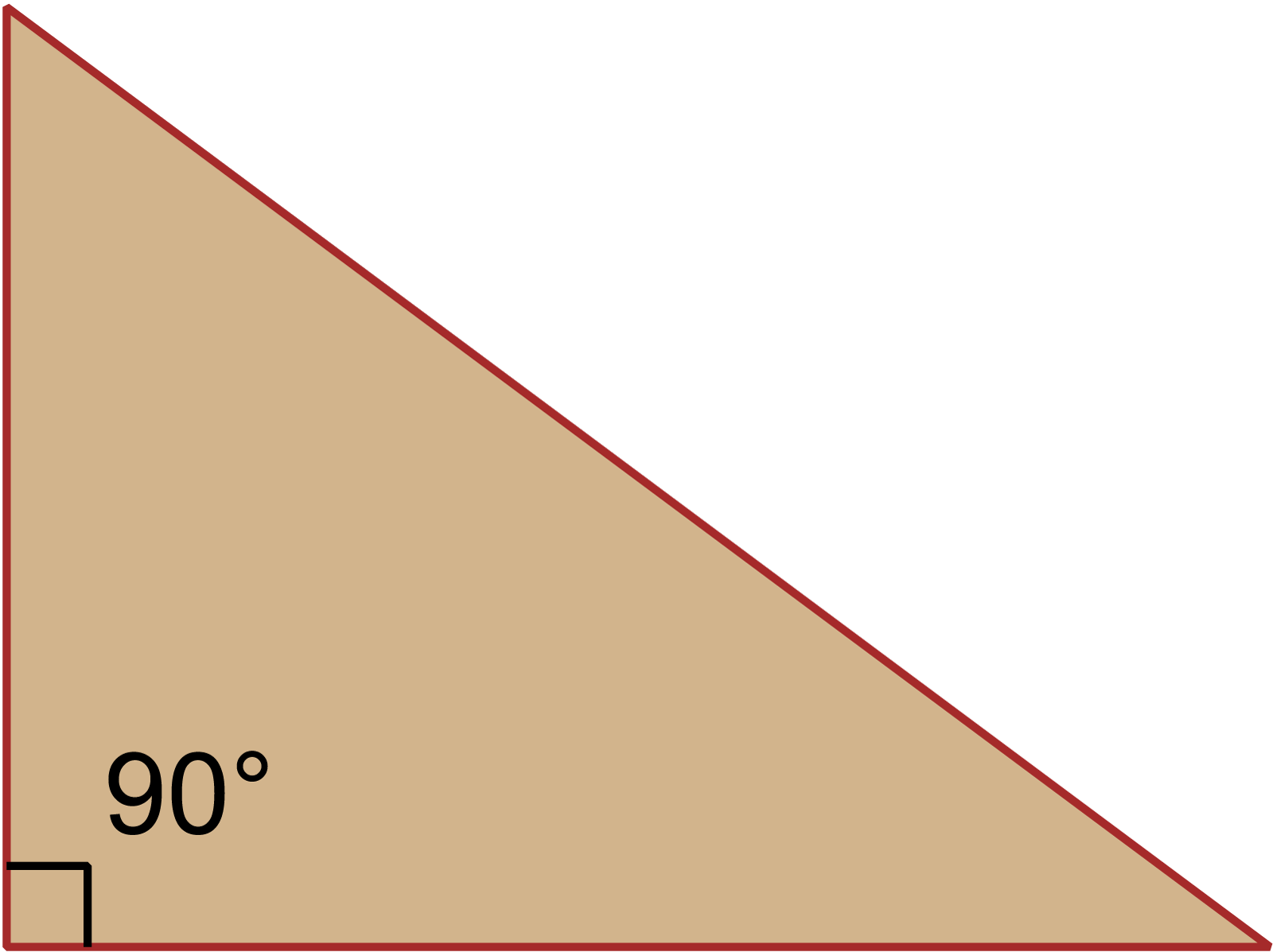
মনেকরি, △ABC একটি সমকোণী ত্রিভুজ যার সমকোণ সংলগ্ন বাহুর দৈর্ঘ্য a একক ও b একক এবং অতিভূজ c একক। তাহলে সমকোণী ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র,
P = (a + b + c) একক।
সমকোণী ত্রিভুজের পরিসীমা P একক হলে,
P = (লম্ব + ভূমি + অতিভূজ) একক।
সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা
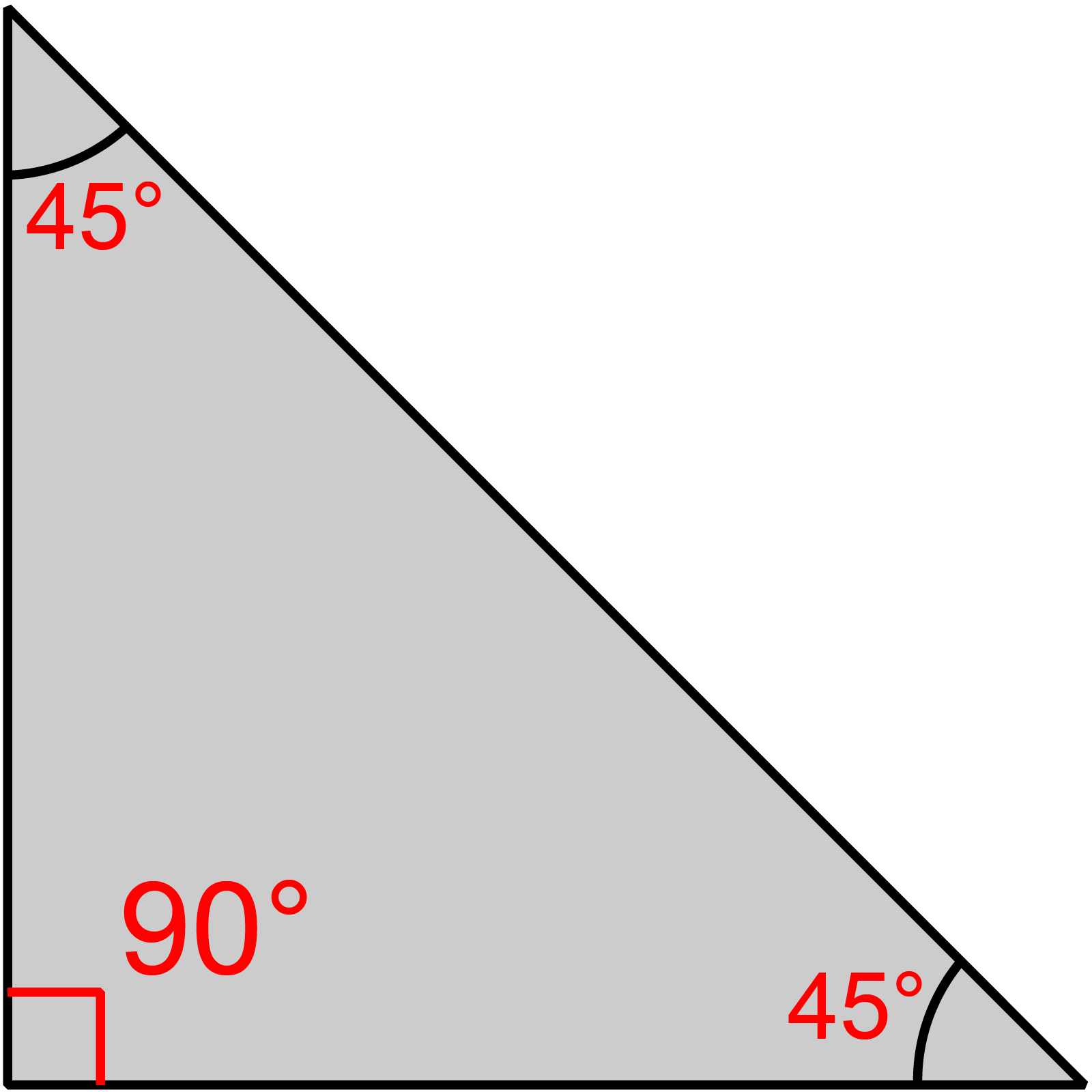
সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভূজ ও সমকোণ সংলগ্ন যেকোনো একটি বাহুর দ্বিগুণের সমষ্টিকে সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা বলে। যেহেতু সমকোণী সমদ্বিবাহু ত্রিভুজ একটি সমদ্বিবাহু ত্রিভুজ যার সমকোণ সংলগ্ন বাহু দুইটি সমান, সেই কারণে এই বাহু দুইটির একটিকে দ্বিগুণ করে তার সাথে অতিভূজ যোগ করলে সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা পাওয়া যায়।
মনেকরি, △ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার সমকোণ সংলগ্ন বাহুর দৈর্ঘ্য b একক, অতিভূজ a একক এবং পরিসীমা P একক। তাহলে, সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমার সূত্র,
P = (a + b + b) একক
অর্থাৎ, P = (a + 2b) একক।
সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা P একক হলে,
P = অতিভূজ + ২ ×(সমকোণ সংলগ্ন একটি বাহ) একক।
ত্রিভুজের পরিসীমার সূত্র
ত্রিভুজের পরিসীমার সূত্র ব্যবহার করে ত্রিভুজের পরিসীমা নির্ণয় করা হয়। ত্রিভুজের পরিসীমা নির্ণয় করার জন্য সাধারণতঃ যেসব ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র ব্যবহার করা হয় তা একটি তালিকা আকারে নিচে দেওয়া হলো।
| ত্রিভুজের নাম | বাহু | ত্রিভুজের পরিসীমার সূত্র |
|---|---|---|
| যেকোনো ত্রিভুজ | ১ম বাহু, ২য় বাহ, ৩য় বাহু | (১ম বাহু + ২য় বাহ + ৩য় বাহু) একক |
| বিষমবাহু ত্রিভুজ | a, b, c | (a + b + c) একক |
| সমদ্বিবাহু ত্রিভুজ | সমান বাহু a, ভূমি b | (2a + b) একক |
| সমবাহু ত্রিভুজ | a | 3a একক |
| সমকোণী ত্রিভুজ | লম্ব, ভূমি, অতিভূজ | (লম্ব + ভূমি + অতিভূজ) একক |
| সমকোণী ত্রিভুজ | সমকোণ সংলগ্ন বাহু b ও c, অতিভূজ a | (a + b + c) একক |
| সমকোণী সমদ্বিবাহু ত্রিভুজ | সমকোণ সংলগ্ন একটি বাহু, অতিভূজ | অতিভূজ + ২ ×(সমকোণ সংলগ্ন একটি বাহু) একক |
| সমকোণী সমদ্বিবাহু ত্রিভুজ | সমকোণ সংলগ্ন একটি বাহু b, অতিভূজ a | (a + 2b) একক |