পূরক কোণ ও পূরক কোণ কাকে বলে
এই টিউটোরিয়ালটি শেষে -
পূরক কোণ বর্ণনা করতে পারা যাবে।
পূরক কোণ কাকে বলে চিত্র সহ ব্যাখ্যা করতে পারা যাবে।
পূরক কোণ কি উদাহরণসহ অঙ্কন করতে পারা যাবে।
পূরক কোণের বৈশিষ্ট্য বিশ্লেষণ করতে পারা যাবে।
সমকোণী ত্রিভুজের পূরক কোণ এর বৈশিষ্ট্য উল্লেখ করতে পারা যাবে।
পূরক কোণের কতকগুলো অভেদাবলী প্রমাণ করতে পারা যাবে।
পূরক কোণ কাকে বলে
দুইটি কোণের সমষ্টি ৯০° বা এক সমকোণ হলে কোণ দুইটির একটিকে অপরটির পূরক কোণ বলে।
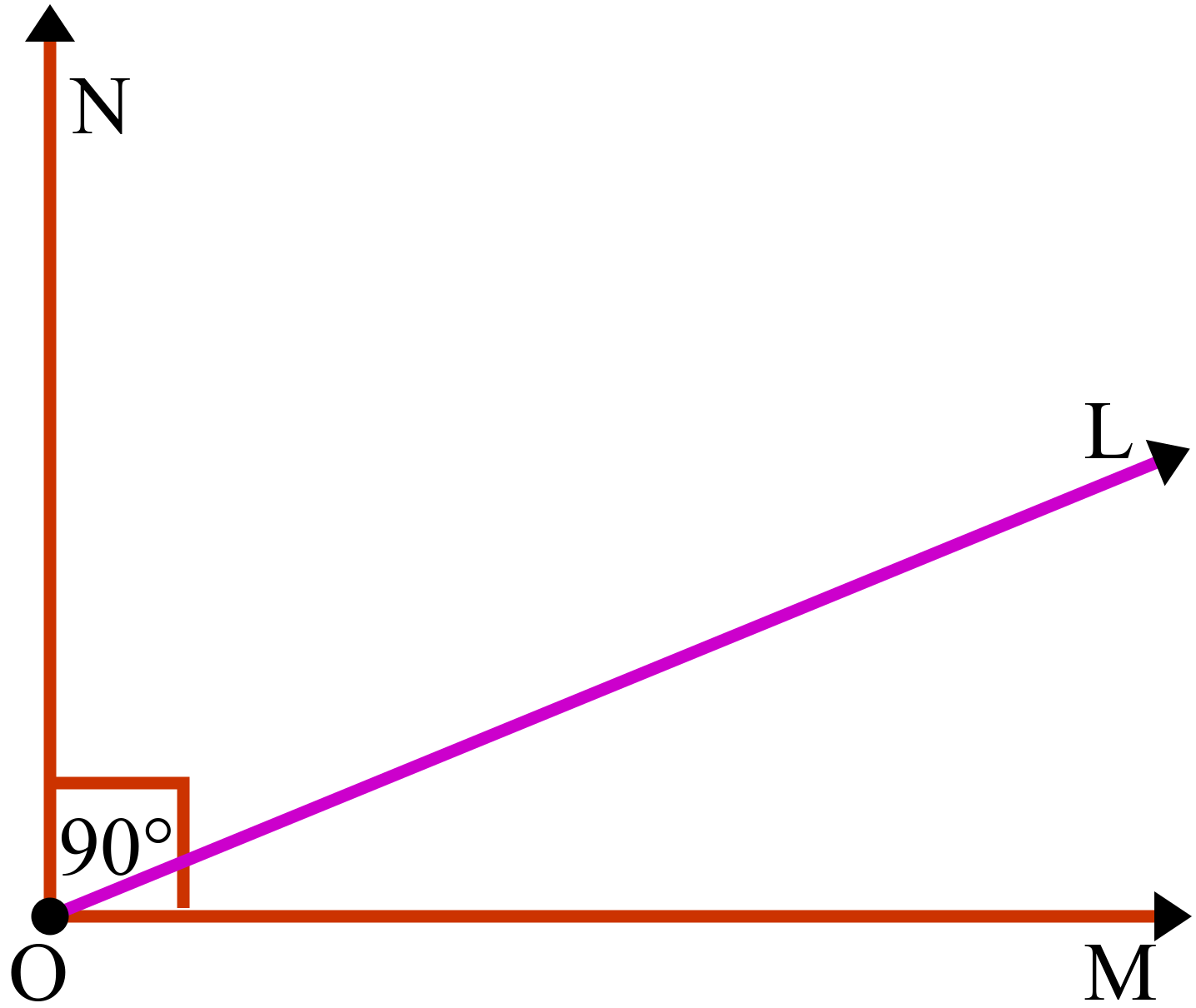
চিত্রে, OL রশ্মি এবং OM রশ্মি পরস্পর O বিন্দুতে মিলিত হয়েছে এবং O বিন্দুতে ∠MOL উৎপন্ন করেছে। আবার, OL রশ্মি এবং ON রশ্মি একত্রে O বিন্দুতে মিলিত হয়েছে এবং O বিন্দুতে ∠LON উৎপন্ন করেছে।
এখন, ∠MOL + ∠LON = ∠MON
∴ ∠MOL + ∠LON = ৯০° [∵ ∠MON = ৯০°]
দেখা যাচ্ছে যে, ∠MOL ও ∠LON কোণ দুইটির যোগফল এক সমকোণ বা ৯০°।
সুতরাং, ∠MOL ও ∠LON কোণ দুইটি পরস্পর পূরক কোণ।
তাছাড়া, এই পূরক কোণ দুইটি পরস্পর সন্নিহিত কোণও বটে।
আবার, পূরক কোণ দুইটির সাধারণ বাহু হলো OL. কোণদ্বয়ের অপর বাহু দুইটি OM এবং ON, সাধারণ বিন্দু O তে মিলিত হয়েছে।
গঠনের ভিত্তিতে পূরক কোণ সম্ভাব্য যেসব উপায়ে উৎপন্ন তা নিচে দেওয়া হলোঃ
- সন্নিহিত পূরক কোণ
- বিচ্ছিন্ন পূরক কোণ
সন্নিহিত পূরক কোণ
পূরক কোণদ্বয়ের যদি একটি সাধারণ বাহু থাকে তবে তাদেরকে পরস্পর সন্নিহিত পূরক কোণ বলে।
উপরের চিত্রে, ∠MOL ও ∠LON পূরক কোণ দুইটি একটি সাধারণ বাহু OL এর সাথে গঠিত হয়েছে। অর্থাৎ, এই পূরক কোণদ্বয়ের একটি সাধারণ বাহু OL আছে। তাই এই কোণ দুইটি পরস্পর সন্নিহিত পূরক কোণ।
তাছাড়া, পরস্পর পূরক কোণদ্বয় যদি সন্নিহিত পূরক কোণ হয়, তাহলে সন্নিহিত কোণদ্বয়ের সাধারণ বাহু ব্যতীত অপর যে দুইটি বাহু থাকে তারা পরস্পর লম্ব হয়। উপরের চিত্রে, সন্নিহিত কোণদ্বয়ের সাধারণ বাহু OL ব্যতীত অপর যে দুইটি বাহু থাকে তারা হলো OM ও ON যারা পরস্পর লম্ব।
আবার নিচের ১ম চিত্রে, সন্নিহিত কোণদ্বয়ের সাধারণ বাহু OB বাদে অপর বাহু দুইটি OA এবং OC পরস্পর O বিন্দুতে লম্ব।
বিচ্ছিন্ন পূরক কোণ
পূরক কোণদ্বয়ের যদি একটি সাধারণ বাহু না থাকে তবে তাদেরকে পরস্পর বিচ্ছিন্ন পূরক কোণ বলে।
যেমন ৩য় চিত্রে, ∠HOI এবং ∠JOK কোণ দুইটির যোগফল ৯০°। ফলে তারা পরস্পর পূরক কোণ। কিন্তু কোণ দুইটির মধ্যে কোনো সাধারণ বাহু নেই। একারণে কোণ দুইটি পরস্পর বিচ্ছিন্ন পূরক কোণ।
নিচে বিভিন্ন ধরণের পূরক কোণ তথা সন্নিহিত পূরক কোণ ও বিচ্ছিন্ন পূরক কোণ চিত্র দেওয়া হলোঃ

বিভিন্ন ধরণের পূরক কোণের চিত্র সমূহ দেখা যাচ্ছে।
সমকোণী ত্রিভুজের পূরক কোণ
ইউক্লিডিও জ্যামিতি অনুসারে, একটি সমকোণী ত্রিভুজের সমকোণ ব্যতীত সূক্ষ্মকোণ দুইটির একটি অপরটির পূরক কোণ।
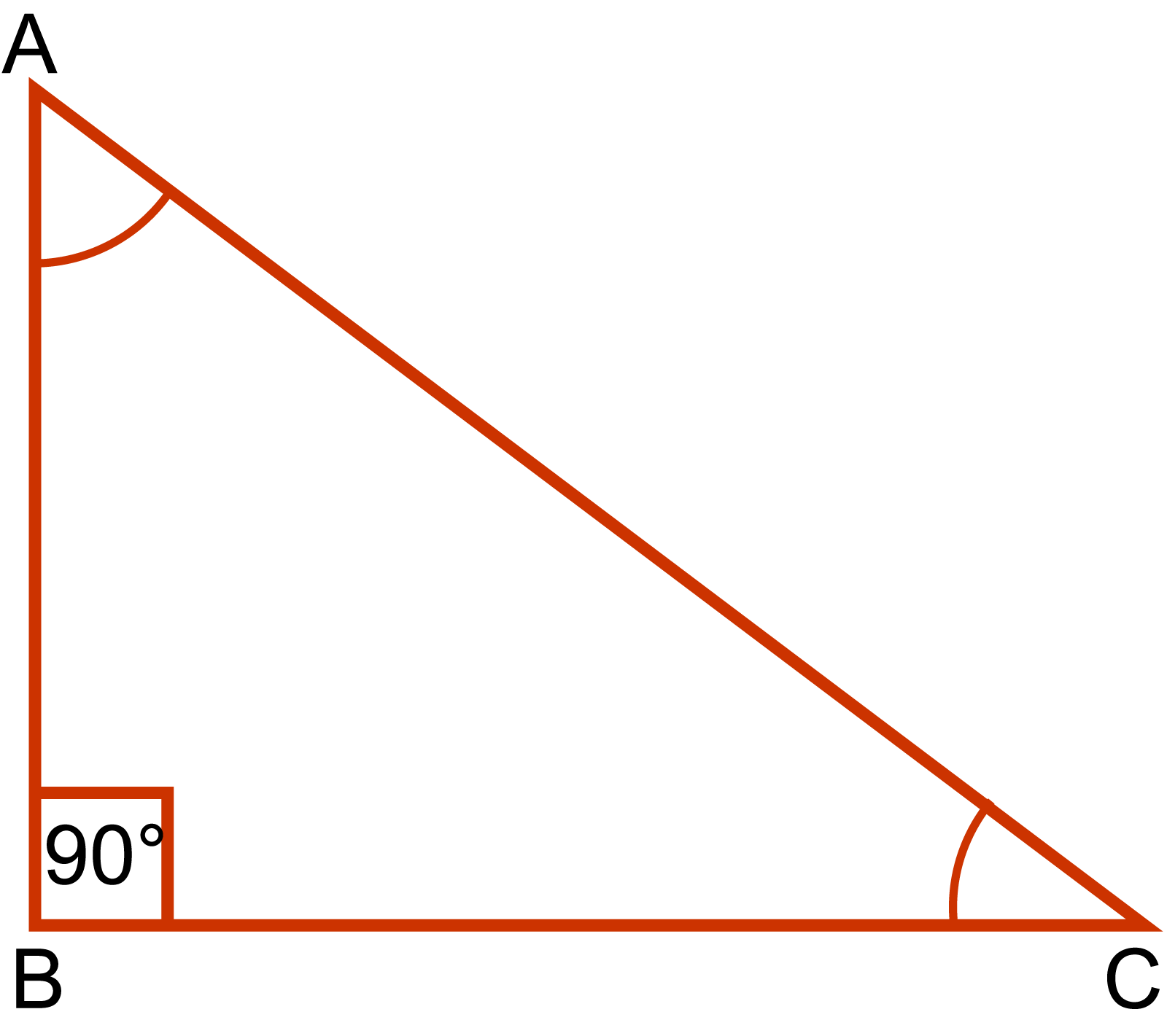
মনেকরি, △ABC একটি সমকোণী ত্রিভুজ যার ∠B = ৯০°। আবার জানা আছে, ত্রিভুজের তিনকোণের সমষ্টি ১৮০°.
∴ ∠A + ∠B + ∠C = ১৮০°
বা, ∠A + ৯০° + ∠C = ১৮০°
বা, ∠A + ∠C = ১৮০° - ৯০°
∴ ∠A + ∠C = ৯০°
অতএব, ∠A এবং ∠C পরস্পর পূরক কোণ।
আবার, একটি কোণ এবং সমকোণ বা ৯০° থেকে ঐ কোণের অন্তর; - এই কোণ দুইটি পরস্পর পূরক। অর্থাৎ, কোনো একটি কোণ ∠D ও (৯০°-∠D) কোণ দুইটি পরস্পর পূরক। লক্ষ্য করি,
∠D + (৯০°-∠D) = ∠D + ৯০°-∠D
বা, ∠D + (৯০°-∠D) = ৯০°
যেহেতু ∠D ও (৯০°-∠D) কোণ দুইটির সমষ্টি ৯০°,
∴ ∠D ও (৯০°-∠D) কোণ দুইটি পরস্পর পূরক কোণ।
পূরক কোণের বৈশিষ্ট্য
পূরক কোণের বৈশিষ্ট্য নির্ণয় করার জন্য পূরক কোণের ধরণ, সমকোণী ত্রিভুজের পূরক কোণ এবং বিভিন্ন ধরণের পূরক কোণের চিত্র বিশ্লেষণ করলে কতকগুলো পূরক কোণ এর বৈশিষ্ট্য পাওয়া যায়। নিম্নে পূরক কোণের বৈশিষ্ট্য দেওয়া হলোঃ
- পূরক কোণ দুইটির সাধারণ বাহু থাকলে সাধারণ বাহু ব্যতীত অপর যে দুইটি বাহু থাকে তারা পরস্পর লম্ব।
- A ও B পরস্পর পূরক কোণ হলে sin2A + sin2B = 1
- পূরক কোণদ্বয়ের বাহু সাধারণ না থাকলেও শীর্ষ সাধারণ হতে পারে।
- কোনো একটি কোণ এবং সমকোণ থেকে ঐ কোণের বিয়োগফল - এই কোণ দুইটি পরস্পর পূরক কোণ।
- A ও B পরস্পর পূরক কোণ হলে cos2A + cos2B = 1
- পূরক কোণদ্বয়ের বাহু সাধারণ থাকতেও পারে; আবার সাধারণ বাহু নাও থাকতে পারে।
- A ও B পরস্পর পূরক কোণ হলে tanA = cotB
- পূরক কোণদ্বয়ের শীর্ষ বিন্দু ভিন্ন হতে পারে।
- পূরক কোণদ্বয়ের সমষ্টি ৯০°।
- পূরক কোণদ্বয়ের শীর্ষ সাধারণ হতেও পারে; আবার শীর্ষ সাধারণ নাও হতে পারে।
- A ও B পরস্পর পূরক কোণ হলে secA = cosecB
- একটি সমকোণী ত্রিভুজের সমকোণ ছাড়া অন্য কোণ দুইটি পরস্পর পূরক কোণ।
পূরক কোণের অভেদাবলী
আবার, ∠x এবং ∠y পরস্পর পূরক কোণ হলে নিচের অভেদাবলী সত্য হয়ঃ
- sin2x + sin2y = 1
- cos2x + cos2y = 1
- tanx = coty
- secx = cosecy
উপরের অভেদাবলী প্রমাণ করার চেষ্টা করি। যেহেতু ∠x এবং ∠y পরস্পর পূরক কোণ,
সুতরাং, ∠x + ∠y = 90°
∴ ∠x = 90° - ∠y এবং ∠y = 90° - ∠x.
প্রথম অভেদ, sin2x + sin2y = 1
প্রমাণঃ বামপক্ষ = sin2x + sin2y
বা, বামপক্ষ = sin2x + sin2(90° - x)
বা, বামপক্ষ = sin2x + cos2x
∴ বামপক্ষ = 1 [∵ sin2x + cos2x = 1]
∴ বামপক্ষ = ডানপক্ষ
∴ sin2x + sin2y = 1
দ্বিতীয় অভেদ, cos2x + cos2y = 1
প্রমাণঃ বামপক্ষ = cos2x + cos2y
বা, বামপক্ষ = cos2x + cos2(90° - x)
বা, বামপক্ষ =cos2x + sin2x
∴ বামপক্ষ = 1 [∵ cos2x + sin2x = 1]
∴ বামপক্ষ = ডানপক্ষ
∴ cos2x + cos2y = 1
তৃতীয় অভেদ, tanx = coty
প্রমাণঃ বামপক্ষ = tanx
বা, বামপক্ষ = tan(90° - y)
বা, বামপক্ষ = coty
∴ বামপক্ষ = coty
∴ বামপক্ষ = ডানপক্ষ
∴ tanx = coty
চতুর্থ অভেদ, secx = cosecy
প্রমাণঃ বামপক্ষ = secx
বা, বামপক্ষ = sec(90° - y)
বা, বামপক্ষ = 1cos(90° - y)
বা, বামপক্ষ = 1siny
∴ বামপক্ষ = cosecy
∴ বামপক্ষ = ডানপক্ষ
∴ secx = cosecy