বিপ্রতীপ কোণ এর বৈশিষ্ট্য

বিপ্রতীপ কোণের বৈশিষ্ট্য

জ্যামিতিতে বিপ্রতীপ কোণের সংজ্ঞা ও বিপ্রতীপ কোণের চিত্র বিশ্লেষণ করলে কতকগুলো বিপ্রতীপ কোণ এর বৈশিষ্ট্য পরিলক্ষিত হয়। বিপ্রতীপ কোণের এসব বৈশিষ্ট্য সমূহের মধ্যে কতকগুলো বৈশিষ্ট্য অন্যান্য কোণের মত সাধারণ এবং কতকগুলো বৈশিষ্ট্য অনন্য।

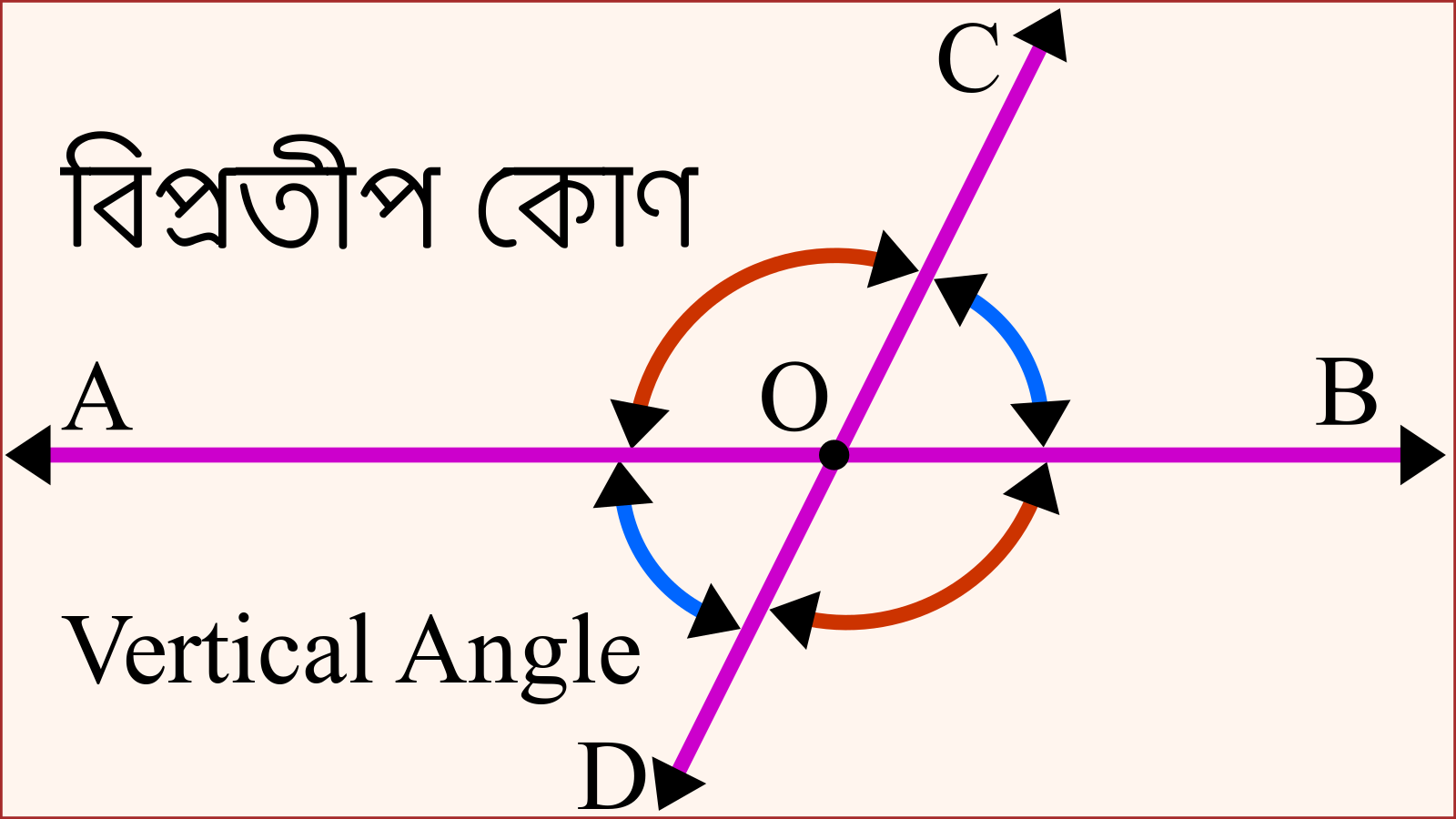
বিপ্রতীপ কোণ বিশ্লেষণ করলে যেসব বিপ্রতীপ কোণের বৈশিষ্ট্য পরিলক্ষিত হয় যেসব বৈশিষ্ট্য সমূহ নিম্নরূপ:

• বিপ্রতীপ কোণ দুইটির শীর্ষবিন্দু সাধারণ হয় অর্থাৎ, দুইটি কোণই একই শীর্ষ বিন্দু থেকে উৎপন্ন হয়।
• বিপ্রতীপ কোণদ্বয় পরস্পর সমান।
• দুইটি সরলরেখা পরস্পর মিলিত হয়ে মিলিত বিন্দুতে যেসব বিপ্রতীপ কোণগুলো উৎপন্ন হয় তাদের সংখ্যা সর্বমোট চারটি।
• বিপ্রতীপ কোণ দুইটির একটি অপরটির বিপরীত দিকে অবস্থান করে।
• দুইটি সরলরেখা পরস্পর মিলিত হয়ে মিলিত বিন্দুতে যে দুইজোড়া বিপ্রতীপ কোণ উৎপন্ন হয়, তাদের মধ্যে একজোড়া বিপ্রতীপ কোণদ্বয়ের প্রত্যেকটি সূক্ষ্মকোণ হলে অপরজোড়া বিপ্রতীপ কোণদ্বয়ের প্রত্যেকটিই স্থূলকোণ হয়।
• দুইটি সরলরেখা পরস্পর ছেদ করলে ছেদ বিন্দুতে যে চারটি বিপ্রতীপ কোণ উৎপন্ন হয়, তাদের মধ্যে যেকোনো একটি কোণের বাহুদ্বয়ের সংলগ্ন কোণ বা সন্নিহিত কোণ দুইটির প্রত্যেকটিই ঐ কোণের সম্পূরক কোণ হয়।
• দুইটি সরলরেখা পরস্পর মিলিত হয়ে মিলিত বিন্দুতে দুইজোড়া বিপ্রতীপ কোণ উৎপন্ন হয়।
• কোনো কোণ এককভাবে কখনও বিপ্রতীপ কোণ হতে পারে না। একই সাথে দুইটি কোণকে বিপ্রতীপ কোণ রূপে প্রকাশ করা যায়। অর্থাৎ, কেবল একই সাথে দুইটি কোণকে একটিকে অপরটির বিপ্রতীপ কোণ বলা যায়।
• দুইটি পরস্পরচ্ছেদী রেখা মিলিত হয়ে মিলিত বিন্দুতে যে দুইজোড়া বিপ্রতীপ কোণ উৎপন্ন হয়, তাদের মধ্যে একজোড়া বিপ্রতীপ কোণদ্বয়ের প্রত্যেকটি সমকোণ হলে অপরজোড়া বিপ্রতীপ কোণদ্বয়ের প্রত্যেকটিও সমকোণ হয়।