রম্বসের পরিসীমার সূত্র
এই টিউটোরিয়ালটি শেষে -
রম্বসের পরিসীমার সূত্র প্রতিপাদন করতে পারা যাবে।
রম্বসের পরিসীমা নির্ণয়ের সূত্র বর্ণনা করতে পারা যাবে।
রম্বসের পরিসীমা নির্ণয় করতে পারা যাবে।
রম্বসের পরিসীমা
রম্বসের বাহুগুলোর সমষ্টিকে রম্বসের পরিসীমা বলে। আর যে সূত্র ব্যবহার করে রম্বসের পরিসীমা নির্ণয় করা হয় তাকে রম্বসের পরিসীমার সূত্র বলে। রম্বস একটি বিশেষ ধরণের চতুর্ভুজ যার চারটি বাহুর দৈর্ঘ্য পরস্পর সমান।
যেহেতু রম্বসের বাহুগুলোর দৈর্ঘ্যের পরিমাপ পরস্পর সমান, তাই রম্বসের একটি বাহুর দৈর্ঘ্য জানা থাকলে এর পরিসীমা নির্ণয় করা যায়।

রম্বসের পরিসীমা নির্ণয়ের সূত্র
রম্বসের চারটি বাহুর দৈর্ঘ্যের সমষ্টি হলো রম্বসের পরিসীমা। তাই রম্বসের পরিসীমার সূত্র প্রতিপাদনের জন্য রম্বসের বাহুগুলোর দৈর্ঘ্য যোগ করতে হয়। আবার, যেহেতু রম্বসের বাহুগুলোর দৈর্ঘ্য পরস্পর সমান, তাই রম্বসের পরিসীমা নির্ণয়ের সূত্র তৈরির জন্য এর একটি বাহুর দৈর্ঘ্যকে চারগুণ করতে হয়।
যেহেতু রম্বসের বাহুগুলোর দৈর্ঘের পরিমাপ পরস্পর সমান, তাই রম্বসের একটি বাহুর দৈর্ঘ্য জানা থাকলে এর পরিসীমা নির্ণয় করা যায়।
রম্বসের পরিসীমার সূত্র নিম্নরূপ:
রম্বসের পরিসীমা = ৪ × (এক বাহু) একক।
নিচে রম্বসের পরিসীমা নির্ণয়ের সূত্র প্রতিপাদন করে দেখানো হলো।
মনে করি, ABCD একটি রম্বস যার AB = BC = CD = AD = a.
আমরা জানি, রম্বসের বাহুগুলো পরস্পর সমান।
সুতরাং, রম্বসের পরিসীমা P হলে,
P = (AB + BC + CD + AD) একক
বা, P = (a + a + a + a) একক
∴ P = 4a একক
একটি রম্বসের এক বাহুর দৈর্ঘ্য a একক হলে রম্বসের পরিসীমা নির্ণয়ের সূত্র হলো:
রম্বসের পরিসীমা = 4a একক।
রম্বসের কর্ণ থেকে পরিসীমা নির্ণয়ের সূত্র
রম্বসের বাহুর দৈর্ঘ্য দেওয়া থাকলে যেমন রম্বসের পরিসীমার সূত্র তৈরি করা যায়; তেমনিভাবে রম্বসের কর্ণ দুইটি জানা থাকলেও রম্বসের পরিসীমা নির্ণয়ের সূত্র উদ্ভাবন করা যায়। এক্ষেত্রে, কর্ণ থেকে প্রথমে বাহুর দৈর্ঘ্য নির্ণয় করা হয়। তারপর এর বাহুর দৈর্ঘ্য থেকে রম্বসের পরিসীমার সূত্র পাওয়া যায়।
রম্বসের কর্ণ থেকে পরিসীমা নির্ণয়ের সূত্র কিভাবে তৈরি করা যায় তা নিচে দেখানো হলো।
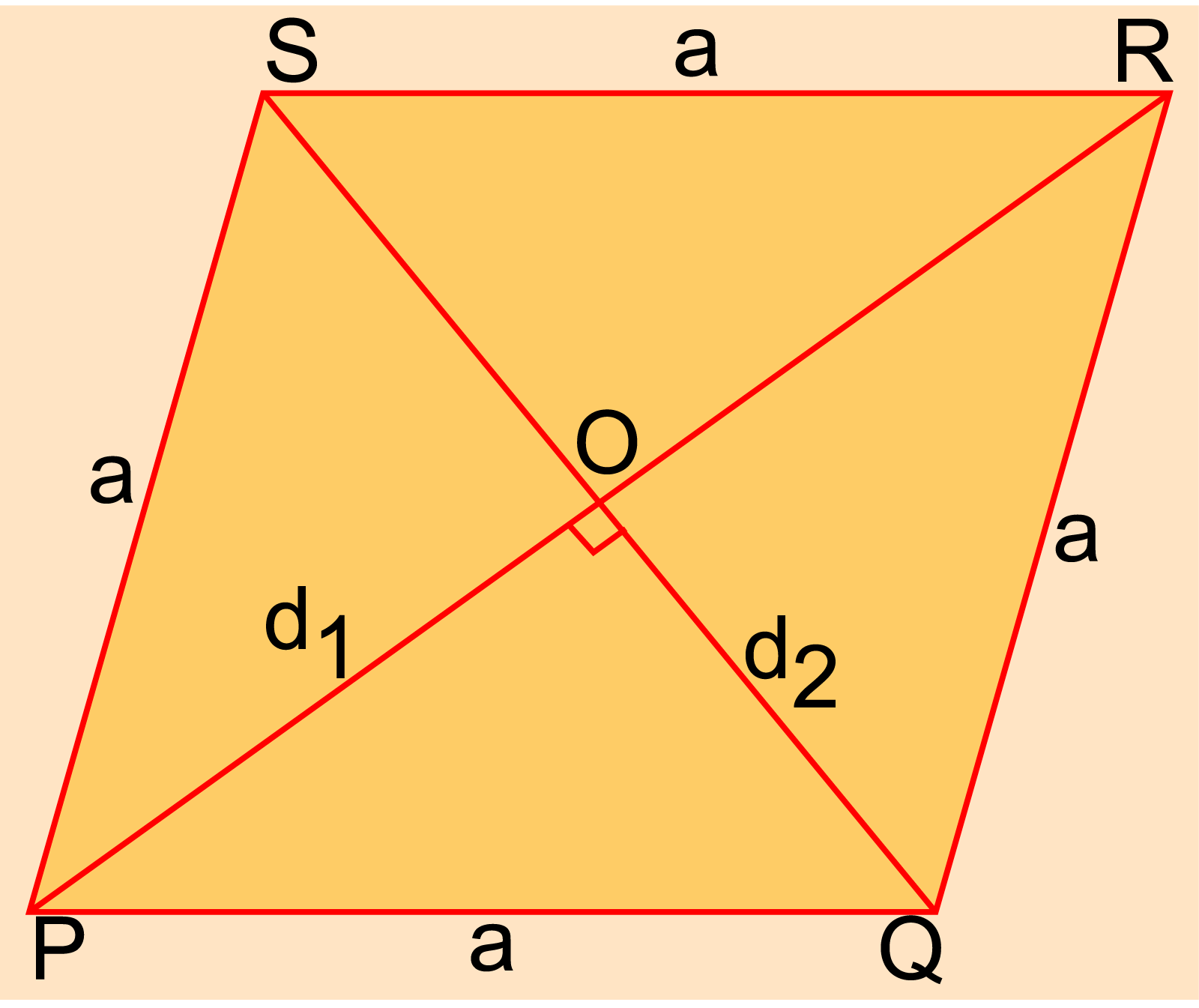
মনে করি, PQRS রম্বসের বাহুগুলোর দৈর্ঘ্য a এবং কর্ণ দুইটি d1 ও d2 পরস্পর o বিন্দেুতে ছেদ করেছে। আমরা জানি, রম্বসের কর্ণ দুইটি পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
∴ OP = d12 এবং OQ = d22
∴ OP2 = d124 এবং OQ2 = d224
আবার, ∠POQ = ৯০°
∴ সমকোণী △POQ থেকে পিথাগোরাসের উপপাদ্য অনুসারে লিখা যায়,
PQ2 = OP2 + OQ2
বা, a2 = d124 + d224
বা, a2 = d12 + d224
বা, a = √d12 + d22√4
∴ a = √d12 + d222
এখন,
রম্বসের পরিসীমা = 4a একক।
বা, রম্বসের পরিসীমা = 4×√d12 + d222 একক।
বা, রম্বসের পরিসীমা = 2×2×√d12 + d222 একক।
∴ রম্বসের পরিসীমা = 2(√d12 + d22) একক।
একটি রম্বসের কর্ণ দুইটির দৈর্ঘ্য d1 ও d2 একক হলে রম্বসের পরিসীমার সূত্র নিম্নরূপ:
রম্বসের পরিসীমা = 2(√d12 + d22) একক।
সমাধান: আমরা জানি, একটি রম্বসের দুইটি কর্ণের দৈর্ঘ্য d1 ও d2 একক হলে,
রম্বসের পরিসীমা = 2(√d12 + d22) একক।
মনে করি, রম্বসটির কর্ণ দুইটির দৈর্ঘ্য d1 = 24 সেমি ও d2 = 10 সেমি।
রম্বসের পরিসীমা = 2(√d12 + d22) একক।
বা, রম্বসের পরিসীমা = 2(√242+ 102) সেমি।
বা, রম্বসের পরিসীমা = 2(√576+ 100) সেমি।
বা, রম্বসের পরিসীমা = 2(√676) সেমি।
বা, রম্বসের পরিসীমা = (2×26) সেমি।
∴ রম্বসের পরিসীমা = 52 সেমি।
সুতরাং, রম্বসটির পরিসীমা 52 সেমি।
সচরাচর যেসব প্রশ্ন করা হয়ে থাকে - Frequently Asked Questions (FAQ)
রম্বসের পরিসীমার সূত্র - সংক্রান্ত সচরাচর যেসব প্রশ্নসমূহ মানুষ করে থাকে।
উত্তরঃ রম্বসের পরিসীমা হলো রস্বসের বাহুগুলোর যোগফল। রম্বসের চারটি বাহুর দৈর্ঘ্য পরস্পর সমান। তাই রম্বসের পরিসীমার সূত্র হলো,
রম্বসের পরিসীমা = ৪×(এক বাহু) একক।
আবার, একটি রম্বসের এক বাহুর দৈর্ঘ্য a একক হলে রম্বসের পরিসীমা নির্ণয়ের সূত্র হলো:
রম্বসের পরিসীমা = 4a একক।
উত্তরঃ একটি রম্বসের কর্ণ দুইটির দৈর্ঘ্য d1 ও d2 একক হলে রম্বসের কর্ণ থেকে পরিসীমা নির্ণয়ের সূত্র নিম্নরূপ:
রম্বসের পরিসীমা = 2(√d12 + d22) একক।