সমকোণী ত্রিভুজ কাকে বলে
এই টিউটোরিয়ালটি শেষে ...
সমকোণী ত্রিভুজ কাকে বলে তা বর্ণনা করতে পারা যাবে।
সমকোণী ত্রিভুজের বৈশিষ্ট্য বিশ্লেষণ করতে পারা যাবে।
সমকোণী ত্রিভুজের ক্ষেত্রফল নির্ণয় করতে পারা যাবে।
সমকোণী ত্রিভুজের বাহুগুলোর অনুপাত কত তা বিশ্লেষণ করতে পারা যাবে।
সমকোণী সমদ্বিবাহু ত্রিভুজ ব্যাখ্যা করতে পারা যাবে।
সমকোণী ত্রিভুজ
যে ত্রিভুজের একটি কোণ সমকোণ বা ৯০° তাকে সমকোণী ত্রিভুজ বলে।
সমকোণী ত্রিভুজের সমকোণ ছাড়া অবশিষ্ট দুইটি কোণের প্রত্যেকটি কোণই এক একটি সূক্ষ্মকোণ।
এই ত্রিভুজের সমকোণ ছাড়া সূক্ষ্মকোণ দুইটির সমষ্টি অবশ্যই ৯০°।
আবার ত্রিভুজের তিনটি কোণের সমষ্টি দুই সমকোণ বা ১৮০° হওয়ার কারণে কোনো ত্রিভুজের একাধিক সমকোণ থাকতে পারে না।
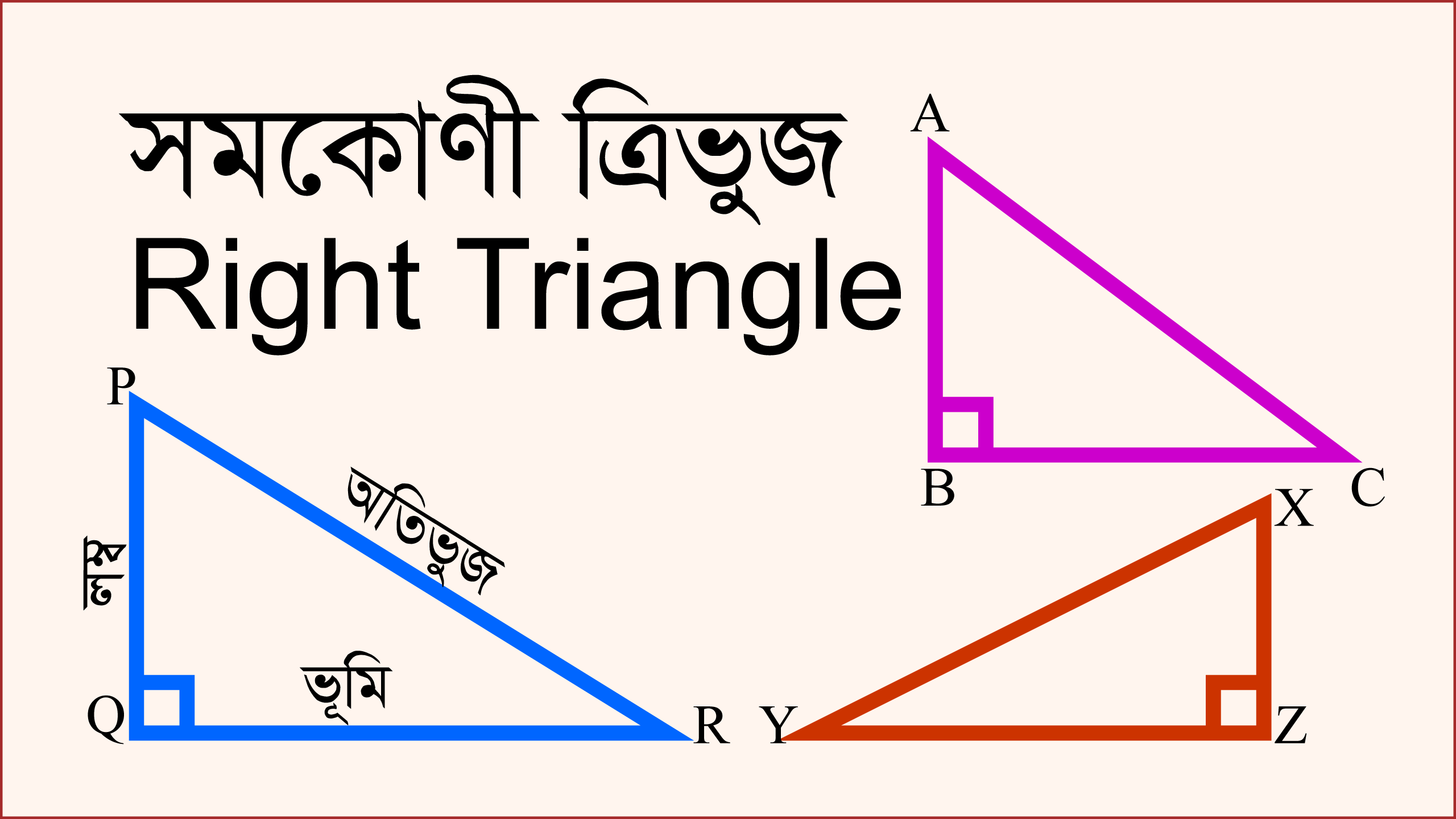
সমকোণ সংলগ্ন বাহু দুইটি সমকোণী ত্রিভুজের পা (legs) বলে পরিচিত। এই পা দুইটিকেই সমকোণী ত্রিভুজের লম্ব ও ভূমি বলে। পা দুইটির একটি ভূমি হলে অপরটি লম্ব হয়।
অন্যদিকে সমকোণের বিপরীত বাহুকে সমকোণী ত্রিভুজের অতিভুজ (hypotenuse) বলে। অতিভুজই সমকোণী ত্রিভুজের বৃহত্তম বাহু।
কোণ বিবেচনায় যে কয় ধরণের ত্রিভূজ আছে, সমকোণী ত্রিভুজ তাদের মধ্যে অন্যতম।
সমকোণী ত্রিভুজ উদাহরণ
সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য পূর্ণসংখ্যাও হতে পারে; আবার ভগ্নাংশ বা দশমিক সংখ্যাও হতে পারে। যদি কোনো সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্যকে পূর্ণসংখ্যায় প্রকাশ করা যায় তাহলে ঐ সমকোণী ত্রিভুজকে ’পিথাগোরীয় ত্রিভুজ’ বলে। আর বাহুগুলোর দৈর্ঘ্যত্রয়কে ‘পিথাগোরীয় ত্রয়’ (Pythagorean Tripple) বলে।
যেমন: একটি সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য ৩, ৪, ৫ হতে পারে। তাহলে ঐ সমকোণী ত্রিভুজটিকে ’পিথাগোরীয় ত্রিভুজ’ বলে। আর ৩, ৪, ৫ হলো ‘পিথাগোরীয় ত্রয়’ বা পিথাগোরীয় ত্রিপল। পিথাগোরীয় ত্রয়কে(৩,৪,৫) লিখে প্রকাশ করা হয়। এরকম আরও অনেক ‘পিথাগোরীয় ত্রয়’ রয়েছে। যেমন - (৫,১২,১৩), (৬৫,৭২,৯৭), (৬৮,২৮৫,২৯৩) ইত্যাদিও এক-একটি ‘পিথাগোরীয় ত্রয়’।
সমকোণী ত্রিভুজের অতিভুজের সূত্র
একটি সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ বলে। সমকোণী ত্রিভুজের অতিভুজের সূত্র প্রতিপাদন করতে হলে পিথাগোরাসের উপপাদ্য সম্পর্কে জ্ঞান থাকা আবশ্যক। আর পিথাগোরাসের উপপাদ্য সমকোণী ত্রিভুজের উপর ভিত্তি করে গড়ে উঠেছে। পিথাগোরাসের উপপাদ্যটি হলো “একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল তার অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলদ্বয়ের সমষ্টির সমান।”
মনেকরি, একটি সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটির দৈর্ঘ্য a ও b এবং অতিভুজের দৈর্ঘ্য c. তাহলে,
c2 = a2+b2
∴ c = √a2 + b2
∴ সমকোণী ত্রিভুজের অতিভুজের সূত্র = √a2 + b2
∴ সমকোণী ত্রিভুজের অতিভুজের সূত্র = √(সমকোণ সংলগ্ন বাহু দুইটির বর্গের সমষ্টি)
সমকোণী ত্রিভুজের ক্ষেত্রফল
যেকোনো ত্রিভুজের ভূমি ও উচ্চতার গুণফলের অর্ধেকই হলো ঐ ত্রিভুজের ক্ষেত্রফল।
অর্থাৎ, ত্রিভুজের ক্ষেত্রফল = ( ১২× ভূমি × উচ্চতা ) বর্গ একক।
সমকোণী ত্রিভুজের ক্ষেত্রেও একই নিয়ম প্রযোজ্য। সমকোণী ত্রিভুজের পা (legs) দুইটি, সমকোণী ত্রিভুজের লম্ব ও ভূমি।
∴ সমকোণী ত্রিভুজের ক্ষেত্রফল = ( ১২× সমকোণ সংলগ্ন বাহুদ্বয়ের গুণফল ) বর্গ একক।
মনে করি, সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটি a ও b.
সেক্ষেত্রে, সমকোণী ত্রিভুজের ক্ষেত্রফল = ১২ ab বর্গ একক।
সমকোণী ত্রিভুজের পরিসীমা
সমকোণী ত্রিভুজের পরিসীমা বলতে সমকোণী ত্রিভুজের বাহু তিনটির সমষ্টিকে বুঝায়। একটি সমকোণী ত্রিভুজের অতিভুজ ও সমকোণ সংলগ্ন বাহুদ্বয়ের সমষ্টিকে সমকোণী ত্রিভুজের পরিসীমা বলে।
সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুইটি a একক ও b একক এবং অতিভুজ c একক হলে,
সমকোণী ত্রিভুজের পরিসীমা = (a + b + c) একক।
আবার অন্যভাবে বললে, একটি সমকোণী ত্রিভুজের লম্ব a একক, ভূমি b একক এবং অতিভুজ c একক হলে,
সমকোণী ত্রিভুজের পরিসীমা = (লম্ব + ভূমি + অতিভুজ) একক।
∴ সমকোণী ত্রিভুজের পরিসীমা = (a + b + c) একক।
একটি সমকোণী ত্রিভুজের লম্ব ও ভূমি যথাক্রমে a একক ও b একক এবং অতিভুজ c একক হলে,
সমকোণী ত্রিভুজের পরিসীমা = (লম্ব + ভূমি + অতিভুজ) একক।
অর্থাৎ, সমকোণী ত্রিভুজের পরিসীমা = (a + b + c) একক।
সমকোণী সমদ্বিবাহু ত্রিভুজ কাকে বলে
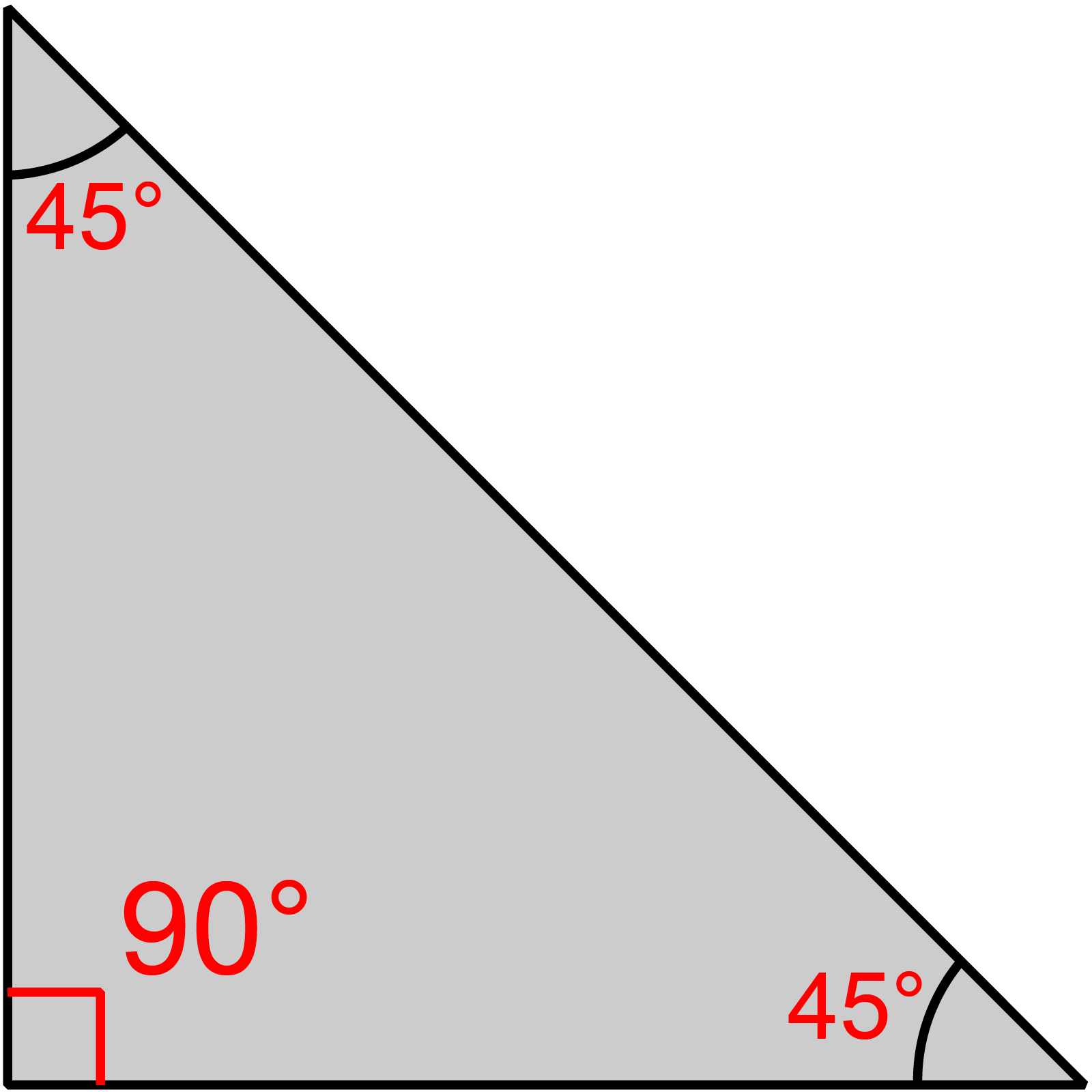
সাধারণভাবে বলা যায়, যে ত্রিভুজ একইসাথে সমদ্বিবাহু ও সমকোণী, তাই সমকোণী সমদ্বিবাহু ত্রিভুজ।
অন্যভাবে বলা যায়, যে সমদ্বিবাহু ত্রিভুজের একটি কোণ ৯০° বা সমকোণ তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে। আর, কোন সমকোণী ত্রিভুজের দুইটি বাহু সমান হলে তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।
সুতরাং, যে ত্রিভুজের দুইটি বাহু সমান ও একটি কোণ সমকোণ তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।
সমকোণী সমদ্বিবাহু ত্রিভুজ এর সমকোণ ব্যতীত অন্য সূক্ষ্মকোণ দুইটি পরস্পর সমান। এই সূক্ষ্মকোণ দুইটির প্রত্যেকটির মান ৪৫°।
অন্যদিকে সমকোণের বিপরীত বাহুকে সমকোণী ত্রিভুজের অতিভুজ (hypotenuse) বলে। অতিভুজই সমকোণী ত্রিভুজের বৃহত্তম বাহু।
সমকোণী ত্রিভুজের বৈশিষ্ট্য
- সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুই হলো অতিভুজ। অতিভুজই সমকোণী ত্রিভুজের বৃহত্তম বাহু।
- সমকোণী ত্রিভুজের বাহুগুলোর দৈর্ঘ্য পূণসংখ্যা হলে তাকে ‘পিথাগোরিয়ান ত্রিপল’(Pythagorean Triple) বলে।
- এই ত্রিভুজের সমকোণ ব্যতীত অন্য দুইটি কোণের সমষ্টি ৯০°।
- সমকোণী ত্রিভুজের সমকৌণিক শীর্ষবিন্দু এবং অতিভুজের মধ্যবিন্দুর সংযোজক রেখাংশ দ্বারা ত্রিভুজটি যে দুইটি ত্রিভুজে বিভক্ত হয়, তারা উভয়ই সমদ্বিবাহু ত্রিভুজ।
- যে কোন দুইটি বাহু জানা থাকলে সমকোণী ত্রিভুজের অন্য বাহুটির দৈর্ঘ্য নির্ণয় করা যায়।
- সমকোণী ত্রিভুজই পিথাগোরাসের উপপাদ্যের ভিত্তি।
- সমকোণী ত্রিভুজের শীর্ষবিন্দুত্রয় দিয়ে অতিক্রান্ত বৃত্ত অঙ্কন করলে ঐ বৃত্তের ব্যাস অতিভুজের সমান।
- এই ত্রিভুজের একটি কোণ ও কোণ সংলগ্ন একটি বাহু জানা থাকলে অন্য সবগুলো বাহু ও কোণগুলো নির্ণয় করা যায়।
- সমকোণী সমদ্বিবাহু ত্রিভুজ এর সমকোণ সংলগ্ন যেকোন বাহু ও অতিভুজের অনুপাত সবসময়ই ১:√২।
- সমকোণী সমদ্বিবাহু ত্রিভুজ এর পা(legs) অর্থাৎ সমকোণ সংলগ্ন বাহু দুইটি পরস্পর সমান এবং অতিভুজ যেকোন একটি পা এর √২ গুণ।
- সমকোণী ত্রিভুজের সমকৌণিক শীর্ষবিন্দু এবং অতিভুজের মধ্যবিন্দুর সংযোজক রেখাংশের দৈর্ঘ্য অতিভুজের অর্ধেক।
- সমকোণী ত্রিভুজের সমকোণ ছাড়া অপর কোণদ্বয়ের একটি আরেকটির দ্বিগুণ হলে ক্ষুদ্রতম কোণের বিপরীত বাহুর দ্বিগুণ অতিভুজের সমান।
- সমকোণী ত্রিভুজের সমকৌণিক শীর্ষ থেকে অতিভুজের উপর লম্ব অঙ্কন করলে অতিভুজ যে দুইটি অংশে বিভক্ত হয় সেই অংশ দুইটি এবং সংশ্লিষ্ট অংশ সংবলিত ত্রিভুজ দুইটির ক্ষেত্রফলদ্বয় সমানুপাতিক।
সচরাচর যেসব প্রশ্ন করা হয়ে থাকে - Frequently Asked Questions (FAQ)
সমকোণী ত্রিভুজ বিষয়ক সচরাচর যেসব প্রশ্নসমূহ মানুষ করে থাকে।
উত্তরঃ যে ত্রিভুজের একটি কোণ সমকোণ বা ৯০° তাকে সমকোণী ত্রিভুজ বলে। ত্রিভুজের তিনটি কোণের যোগফল ১৮০° ব’লে একটি সমকোণী ত্রিভুজের একটি কোণ ৯০° হওয়ার কারণে অপর দুইটি কোণের যোগফল ৯০°। এজন্য একটি সমকোণী ত্রিভুজের সমকোণ ছাড়া অপর দুইটি কোণ অবশ্যই সূক্ষ্মকোণ।
উত্তরঃ সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ বলে। অতিভুজই একটি সমকোণী ত্রিভুজের বৃহত্তম বাহু।
উত্তরঃ একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল তার অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলদ্বয়ের সমষ্টির সমান।
অর্থাৎ, (অতিভুজ)² = (লম্ব)² + (ভূমি)²
∴ অতিভুজ = √ (লম্ব)2 + (ভূমি)2
অতএব, একটি সমকোণী ত্রিভুজের লম্ব a একক, ভূমি b একক এবং অতিভুজ c একক হলে
অতিভুজ c = √ a2 + b2 একক।
উত্তরঃ সমকোণী ত্রিভুজের লম্ব, ভূমি ও অতিভুজের সমষ্টিকে সমকোণী ত্রিভুজের পরিসীমা বলে। একটি সমকোণী ত্রিভুজের যেকোনো দুইটি বাহুর দৈর্ঘ্য জানা থাকলে এর পরিসীমা নির্ণয় করা যায়।
উত্তরঃ সমকোণী ত্রিভুজের পরিসীমার সূত্র প্রতিপাদনের পূর্বে এর বাহুগুলোর নাম জানা দরকার। সমকোণী ত্রিভুজের বাহু তিনটির নাম হলো লম্ব, ভূমি ও অতিভুজ।
সমকোণী ত্রিভুজের পরিসীমা = (লম্ব + ভূমি + অতিভুজ) একক।
একটি সমকোণী ত্রিভুজের লম্ব a একক, ভূমি b একক এবং অতিভুজ c একক হলে,
সমকোণী ত্রিভুজের পরিসীমা = (a + b + c) একক।
উত্তরঃ সমকোণী ত্রিভুজের বৃহত্তম বাহুর নাম হলো অতিভুজ। যেকোনো সমকোণী ত্রিভুজের অতিভুজই হলো বৃহত্তম বাহু।
উত্তরঃ সমকোণী ত্রিভুজের সমকোণ ছাড়া অপর দুইটি কোণের পরিমানের সমষ্টি ৯০°। অতএব, এই দুইটি কোণের একটি ৬০° হলে অপর কোণটি হবে (৯০° - ৬০°) = ৩০°
∴ সমকোণ ছাড়া অপর দুইটি কোণের অনুপাত = ৬০°:৩০°
অর্থাৎ, সমকোণ ছাড়া অপর দুইটি কোণের অনুপাত = ২:১
অথবা, সমকোণ ছাড়া অপর দুইটি কোণের অনুপাত = ১:২
উত্তরঃ সমকোণী ত্রিভুজের সমকোণ ব্যতীত অবশিষ্ট কোণ দুইটির সমষ্টি ৯০°। সমকোণ ব্যতীত অন্য দুইটি কোণের সমষ্টি ৯০° হওয়ার কারণে এদের প্রত্যেকেই ৯০° অপেক্ষা কম অর্থাৎ, প্রত্যেকেই এক-একটি সূক্ষ্মকোণ। অতএব, এই দুইটি কোণই সূক্ষ্মকোণ। সুতরাং, একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণ সংখ্যা দুইটি। অর্থাৎ, একটি সমকোণী ত্রিভুজের দুইটি কোণ সূক্ষ্মকোণ।