সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র

সামান্তরিক জাতীয় বস্তুর পরিসীমা পরিমাপ করতে হলে সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র সম্পর্কে সম্মক জ্ঞান থাকা জরুরী। একটি সামান্তরিকের চারদিকের সীমানার দৈর্ঘ্যই হলো এর পরিসীমা। আরও ভালভাবে বললে, সামান্তরিকের চারটি বাহুর দৈর্ঘ্যের সমষ্টিই হলো এর পরিসীমা। আর এই পরিসীমা পরিমাপ করতে সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র ব্যবহার করা হয়। সামান্তরিক হলো বিশেষ ধরণের একটি চতুর্ভুজ যার বিপরীত বাহুগুলো এবং বিপরীত কোণগুলো পরস্পর সমান। সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র প্রয়োগ করে সামান্তরিকের চারটি বাহুর দৈর্ঘ্যের যোগফল বা এর পরিসীমা বের করা হয়।

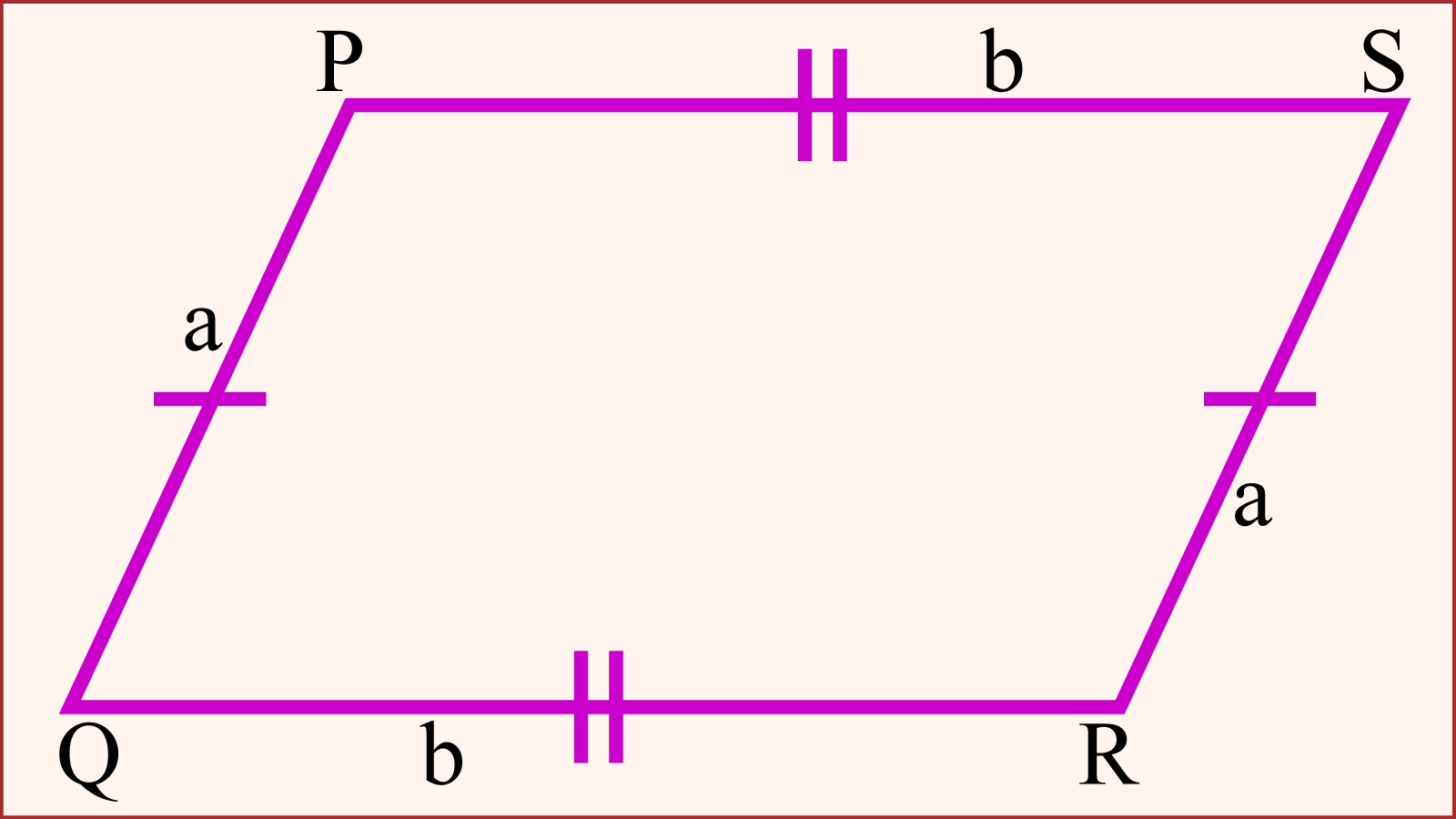
সামান্তরিকের বিপরীত বাহুগুলোর দৈর্ঘ্য পরস্পর সমান। একারণে, সামান্তরিকের একজোড়া সন্নিহিত বাহুর দৈর্ঘ্যের সমষ্টিকে দ্বিগুণ করলে এর পরিসীমা পাওয়া যায়। তাহলে সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র হবে নিম্নরূপ:
সামান্তরিকের পরিসীমা = 2 × (একজোড়া সন্নিহিত বাহুর সমষ্টি) একক।

মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a একক এবং b একক। তাহলে সামান্তরিকের পরিসীমা নির্ণয়ের সূত্রটি হবে নিম্নরূপঃ
সামান্তরিকের পরিসীমা = 2 (a + b) একক।

তাহলে দেখা যাক সামান্তরিকের পরিসীমার সূত্রটি তৈরি করা যায় কিনা!

মনে করি, PQRS একটি সামান্তরিক যার PQ = SR = ‍a এবং QR = PS = b। আমরা, ইতোমধ্যে জেনেছি, সামান্তরিকের পরিসীমা হলো এর চারটি বাহুর দৈর্ঘ্যের যোগফল।
তাহলে, সামান্তরিকের পরিসীমা = (চারটি বাহুর দৈর্ঘ্যের যোগফল) একক
বা, সামান্তরিকের পরিসীমা = (PQ + QR +SR+ PS) একক
বা, সামান্তরিকের পরিসীমা = (a + b + a + b) একক
বা, সামান্তরিকের পরিসীমা = (2a + 2b) একক
∴ সামান্তরিকের পরিসীমা = 2(a + b) একক।

অতএব, সামান্তরিকের ক্ষেত্রফল = 2 × (একজোড়া সন্নিহিত বাহুর যোগফল) একক।

উদাহরণ: একটি সামান্তরিকের সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য 38 সেমি ও 54 সেমি হলে পরিসীমা কত হবে?

সমাধান: মনে করি, সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a = 38 একক ও b = 54 একক। তাহলে, সামান্তরিকের পরিসীমা নির্ণয়ের সূত্র অনুসারে,
সামান্তরিকের পরিসীমা = 2(a + b) একক
বা, সামান্তরিকের পরিসীমা = 2(38 + 54) সেমি
বা, সামান্তরিকের পরিসীমা = (2 × 92) সেমি
∴ সামান্তরিকের পরিসীমা = 184 সেমি

সামান্তরিকের পরিসীমার উপর বিভিন্ন প্রতিযোগিতামূলক পরীক্ষায় আসা কয়েকটি প্রশ্ন