সামান্তরিকের বৈশিষ্ট্য
এই টিউটোরিয়ালটি শেষে ...
সামান্তরিকের বৈশিষ্ট্য সমূহ ব্যাখ্যা করতে পারা যাবে।
সামান্তরিক বিশ্লেষণ করলে কতকগুলো সামান্তরিকের বৈশিষ্ট্য ও মৌলিক উপাদানসমূহ আমাদের চোখের সামনে ভেসে ওঠে। আর সামান্তরিকের এসব বৈশিষ্ট্য সমূহ এর গঠন প্রণালী, বাহুর দৈর্ঘ্য, কোণের পরিমাপ, কর্ণ ইত্যাদি থেকে নিঃসৃত হয়। যেকোনো ধরণের চতুর্ভুজ ও সামান্তরিকের বৈশিষ্ট্য সমূহের মধ্যে বেশকিছু বৈশিষ্ট্য সাধারণ থাকলেও সামান্তরিকের কতকগুলো মৌলিক ও অনন্য বৈশিষ্ট্যও রয়েছে। এসব অনন্য বৈশিষ্ট্য সমূহ সামান্তরিককে অন্যান্য চতুর্ভুজ থেকে আলাদা করেছে।
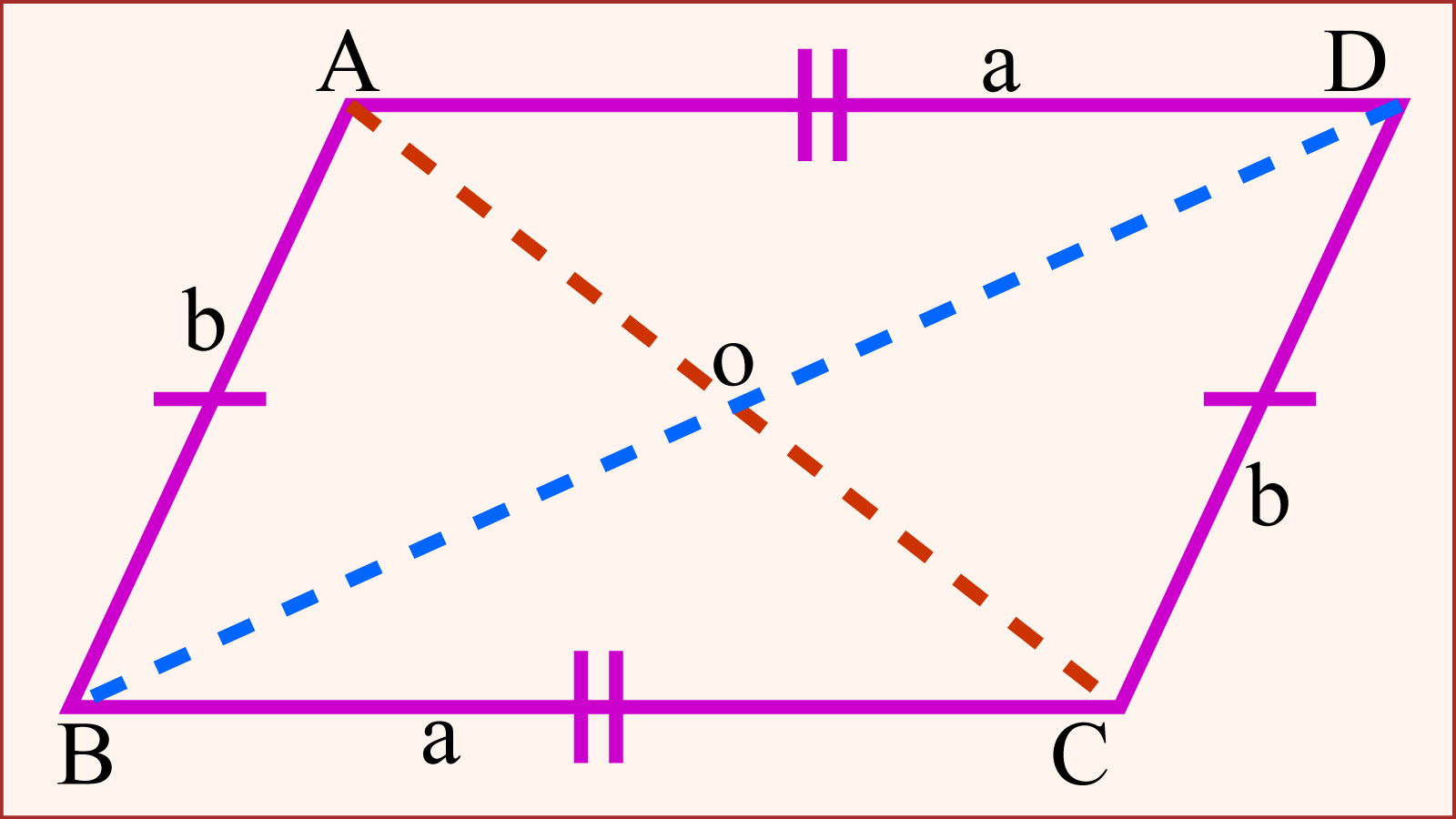
সামান্তরিক হলো অন্যান্য কতকগুলো চতুর্ভুজের সাধারণ রূপ। একারণে কিছু কিছু সামান্তরিকের বৈশিষ্ট্য অন্যান্য চতুর্ভুজের বৈশিষ্ট্যের সাথে মিলে যায়। মজার বিষয় হলো সামান্তরিকের ঐসব বৈশিষ্ট্য জানা থাকলে অন্যান্য সকল চতুর্ভুজের বৈশিষ্ট্য জানা খুবই সহজ হয়ে যায়। জ্যামিতির বেশকিছু মৌলিক ধারণা সামান্তরিকের বৈশিষ্ট্যকে ভিত্তি করে গড়ে উঠেছে। তাছাড়া গণিত ও বিজ্ঞানের বিভিন্ন শাখা-প্রশাখায় সামান্তরিকের বিভিন্ন বৈশিষ্ট্য নানাভাবে ব্যবহৃত হয়।
যাহোক, সামান্তরিক সম্পর্কে আরও বেশি জানতে হলে সামান্তরিকের বৈশিষ্ট্য সম্পর্কে সম্মক জ্ঞান থাকা আবশ্যক। সামান্তরিকের কতকগুলো বৈশিষ্ট্য সমূহ নিচে তুলে ধরা হলো।
- সামান্তরিকের বিপরীত বাহুদ্বয় পরস্পর সমান।
- সামান্তরিকের অন্তঃস্থ কোণ চারটির সমষ্টি চার সমকোণ বা ৩৬০°।
- সামান্তরিকের বিপরীত কোণদ্বয় পরস্পর সমান।
- সামান্তরিকের ভূমিকে উচ্চতা দিয়ে গুণ করলে সামান্তরিকের ক্ষেত্রফল পাওয়া যায়।
- সামান্তরিকের বৈশিষ্ট্য সমূহের মধ্যে একটি গুরুত্বপূর্ণ বৈশিষ্ট্য হলো- সামান্তরিকের যেকোনো দুইটি সন্নিহিত কোণের যোগফল দুই সমকোণ বা ১৮০°।
- সামান্তরিকের ক্ষেত্রফল এর যে কোন কর্ণদ্বারা গঠিত ত্রিভুজক্ষেত্রের ক্ষেত্রফলের দ্বিগুণের সমান।
- সামান্তরিকের বিপরীত বাহুদ্বয় পরস্পর সমান্তরাল।
- সামান্তরিকের ক্ষেত্রফল এর যে কোন কর্ণদ্বারা গঠিত ত্রিভুজক্ষেত্রের ক্ষেত্রফলের দ্বিগুণের সমান।
- সামান্তরিকের কর্ণদ্বয় সবসময়ই সামান্তরিকের অভ্যন্তরে অবস্থান করে।
- সামান্তরিকের কোণগুলো সূক্ষ্মকোণ এবং স্থুলকোণ।
- সামান্তরিকের কর্ণদ্বয় পরস্পর অসমান।
- সামান্তরিকের বৈশিষ্ট্য সমূহের মধ্যে আরেকটি গুরুত্বপূর্ণ বৈশিষ্ট্য হলো- সামান্তরিকের বৃহত্তর কর্ণ সংলগ্ন কোণ দুইটি সূক্ষ্মকোণ।
- সামান্তরিকের সন্নিহিত কোণ দুইটি পরস্পর সম্পূরক কোণ।
- সামান্তরিকের ভূমিকে উচ্চতা দিয়ে গুণ করলে ক্ষেত্রফল পাওয়া যায়।
- সামান্তরিকের প্রত্যকটি কোণ সমকোণ হলে তখন এটি আয়তক্ষেত্র আকার ধারণ করে।
- সামান্তরিকের ক্ষুদ্রতর কর্ণ দ্বারা সামান্তরিকটি যে দুইটি ত্রিভুজে বিভক্ত হয় সেই ত্রিভুজ দুইটির উভয়ই সূক্ষ্মকোণী ত্রিভুজ।
- সামান্তরিকের কর্ণদ্বারা সামান্তরিকটি দুইটি সর্বসম ত্রিভুজে বিভক্ত হয়।
- সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
- সামান্তরিকের কর্ণদ্বয় সবসময়ই সামান্তরিকের অভ্যন্তরে অবস্থান করে।
- সামান্তরিকের সন্নিহিত বাহুদ্বয়ের সমষ্টিকে দ্বিগুণ করলে পরিসীমা পাওয়া যায়।
- সামান্তরিকের বৈশিষ্ট্য সমূহের মধ্যে আরেকটি গুরুত্বপূর্ণ বৈশিষ্ট্য হলো- সামান্তরিকের কর্ণদ্বয়ের উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টি এর বাহুগুলোর উপর অঙ্কিত বর্গক্ষেত্রগুলোর সমষ্টি সমান।
- সামান্তরিকের সবগুলো বাহুর দৈর্ঘ্য পরস্পর সমান হলে তখন এটি রম্বস হয়ে যায়।
- সামান্তরিকের বিপরীত কোণ দুইটির সমষ্টি একটি সূক্ষ্মকোণ বা স্থুলকোণ।
- সামান্তরিকের কর্ণদ্বয়ের উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টি এর বাহুগুলোর উপর অঙ্কিত বর্গক্ষেত্রগুলোর সমষ্টি সমান।
- সামান্তরিকের বৃহত্তর কর্ণ দ্বারা সামান্তরিকটি যে দুইটি ত্রিভুজে বিভক্ত হয় সেই ত্রিভুজ দুইটির উভয়ই স্থুলকোণী ত্রিভুজ।
- সামান্তরিকের কর্ণদ্বয় সামান্তরিকটিকে চারটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে।
- সামান্তরিকের বৈশিষ্ট্য সমূহের মধ্যে আরেকটি গুরুত্বপূর্ণ বৈশিষ্ট্য হলো- সামান্তরিকের একটি কোণের পরিমাপ জানা থাকলে অপর কোণগুলোর পরিমাপ নির্ণয় করা যায়।
- সামান্তরিকের সন্নিহিত বাহু দুইটি a এবং b হলে পরিসীমা = 2(a+b).
- সামান্তরিকের বাহুচারটির উপর অন্তঃস্থ বা বহিঃস্থভাবে অঙ্কিত বর্গক্ষেত্রগুলোর কেন্দ্র হবে কোনো একটি বর্গক্ষেত্রের চারটি শীর্ষ বিন্দু।
- সামান্তরিকের কোণগুলো সমকোণ হলে এবং বাহুগুলো পরস্পর সমান হলে তখন এটি বর্গক্ষেত্র আকার ধারণ করে।
- সামান্তরিকের ক্ষুদ্রতর কর্ণ সংলগ্ন কোণ দুইটি স্থুলকোণ।
- সামান্তরিকের কর্ণদ্বয় পরস্পর সমান হলে তখন এটি আয়তক্ষেত্র হয়ে যায়।