সামান্তরিক কাকে বলে

যে চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান্তরাল তাকে সামান্তরিক বলে। অন্যভাবে বললে, যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল কিন্তু কোণগুলো সমকোণ নয় তাকে সামান্তরিক বলে।

আবার, এভাবে সামান্তরিকের সংজ্ঞা দেওয়া যায়, চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল হলে তাকে সামান্তরিক বলে।

তাহলে সামান্তরিক কাকে বলে - প্রশ্নের সংক্ষিপ্ত উত্তর বা সংক্ষেপে সামান্তরিকের সংজ্ঞা হলো - চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান্তরাল হলে তাকে সামান্তরিক বলে।

সামান্তরিক হলো একটি বিশেষ ধরনের চতুর্ভুজ।

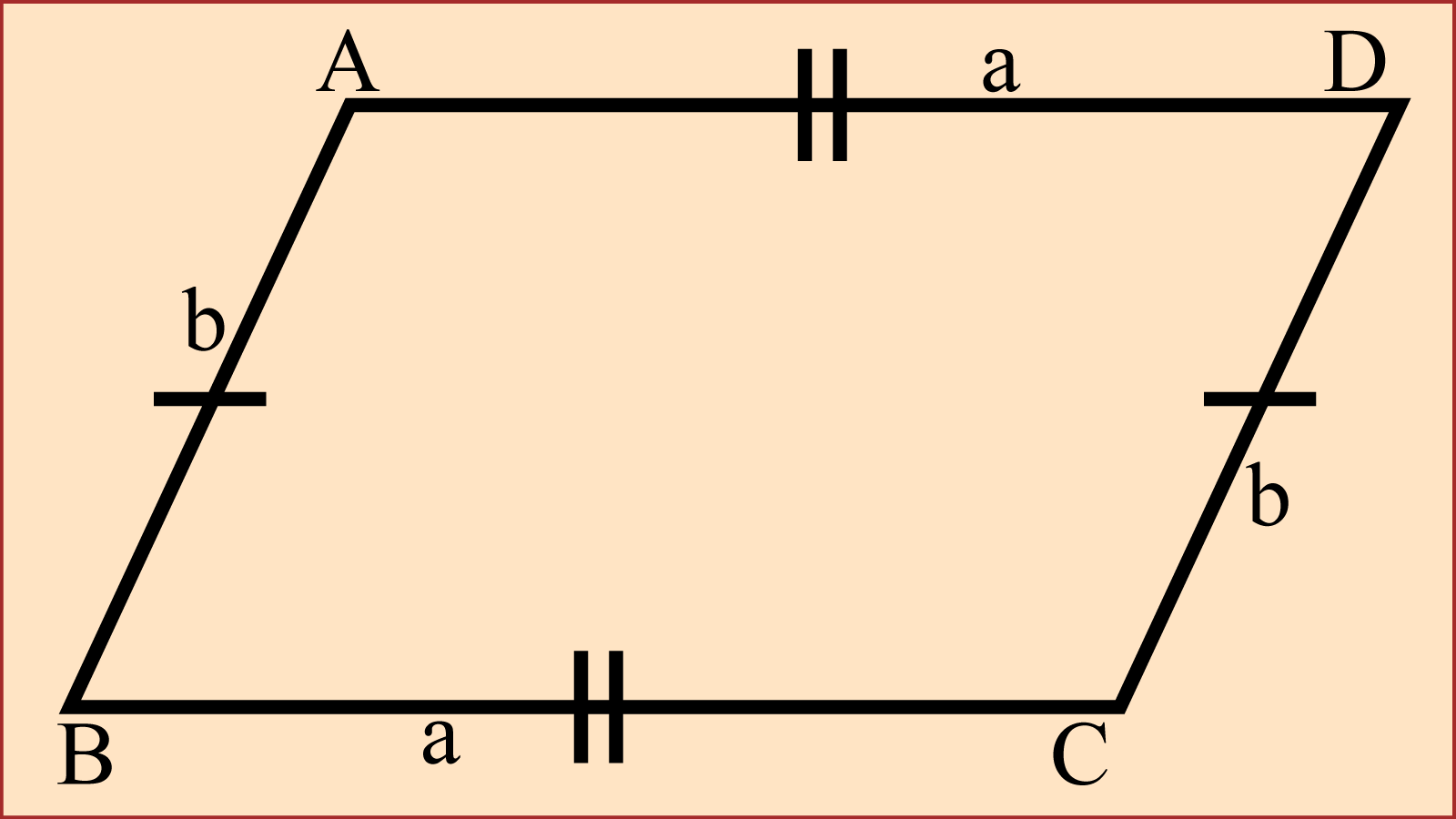
সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান্তরাল। আবার, সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান। সামান্তরিকের বিপরীত কোণগুলোও পরস্পর সমান।

আবার, সামান্তরিকের সন্নিহিত কোণ দুইটি পরস্পর সম্পূরক কোণ। অর্থাৎ, সামান্তরিকের যেকোনো সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ বা ১৮০°।

সামান্তরিকের কর্ণ দুইটি একে-অপরকে সমদ্বিখণ্ডিত করে।

সামান্তরিকের যেকোনো কর্ণ সামান্তরিকটিকে যে দুইটি ত্রিভুজে বিভক্ত করে তারা পরস্পর সর্বসম ত্রিভুজ।

সামান্তরিকের চারটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রগুলোর সমষ্টি তার কর্ণ দুইটির উপর অঙ্কিত বর্গক্ষেত্র দুইটির সমষ্টির সমান।

সামান্তরিকের পরিসীমা

সামান্তরিকের বাহুগুলোর দৈর্ঘ্যের সমষ্টিকে সামান্তরিকের পরিসীমা বলে। অন্যভাবে বললে, সামান্তরিকের চারটি বাহুর যোগফলকে সামান্তরিকের পরিসীমা বলে। যেকোনো সামান্তরিকের সন্নিহিত যেকোনো দুইটি বাহু দেওয়া থাকলে সামান্তরিকের পরিসীমা নির্ণয় করা যায়।

মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a একক এবং b একক।

সুতরাং, সামান্তরিকের পরিসীমার সূত্রটি হবে-

সামান্তরিকের পরিসীমা = (a+b+a+b) একক

বা, সামান্তরিকের পরিসীমা = (2a+2b) একক

∴ সামান্তরিকের পরিসীমা = 2(a+b) একক

∴ সামান্তরিকের পরিসীমা = ২ ⨯(সন্নিহিত বাহুদ্বয়ের সমষ্টি) একক

উদাহরণ: একটি সামান্তরিকের সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য ৯ সেমি ও ৫ সেমি হলে সামান্তরিকের পরিসীমা নির্ণয় কর।

উত্তর: মনেকরি, সামান্তরিকটির সন্নিহিত বাহু দুইটি a = ৯ সেমি এবং b = ৫ সেমি।

আমরা জানি,
সামান্তরিকের পরিসীমা = ২ ⨯(সন্নিহিত বাহুদ্বয়ের সমষ্টি) একক।

∴ সামান্তরিকের পরিসীমা = 2(a+b) একক

বা, সামান্তরিকের পরিসীমা = ২(৯+৫) সেমি

বা, সামান্তরিকের পরিসীমা = (২ ⨯ ১৪) সেমি

∴ সামান্তরিকের পরিসীমা = ২৮ সেমি।

সামান্তরিকের ক্ষেত্রফল

সামান্তরিকের ভূমি ও উচ্চতার গুণফলকে সামান্তরিকের ক্ষেত্রফল বলে।

মনে করি, একটি সামান্তরিকের ভূমি b একক এবং উচ্চতা h একক।

সুতরাং, সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক অর্থাৎ,

সামান্তরিকের ক্ষেত্রফল = (b × h) বর্গ একক

উদাহরণ: একটি সামান্তরিকের ভূমি ২৪ সেমি এবং উচ্চতা ১৬ সেমি হলে সামান্তরিকের ক্ষেত্রফল নির্ণয় কর।

উত্তর: মনেকরি, সামান্তরিকটির ভূমি b = ২৪ সেমি এবং উচ্চতা h = ১৬ সেমি।

আমরা জানি,
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক।

∴ সামান্তরিকের ক্ষেত্রফল =( b × h ) বর্গ একক।

বা, সামান্তরিকের ক্ষেত্রফল =( ২৪ × ১৬ ) বর্গ সেমি।

∴ সামান্তরিকের ক্ষেত্রফল = ৩৮৪ বর্গ সেমি।

সামান্তরিক উদাহরণ

সামান্তরিকের তিনটি বৈশিষ্ট্য

সামান্তরিকের সংজ্ঞা ও চিত্র বিশ্লেষণ করলে কতকগুলো সামান্তরিকের বৈশিষ্ট্য পরিলক্ষিত হয়। নিচে সামান্তরিকের তিনটি বৈশিষ্ট্য উল্লেখ করা হলো।

• সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
• সামান্তরিকের বিপরীত কোণগুলো পরস্পর সমান।
• সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল।

সামান্তরিক কাকে বলে তথা সামান্তরিক বিষয়ক সচরাচর যেসব প্রশ্নসমূহ মানুষ করে থাকে।

যে চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল তাকে সামান্তরিক বলে। সামান্তরিকের বিপরীত বাহুগুলো সমান। তেমনিভাবে, সামান্তরিকের বিপরীত কোণগুলোও পরস্পর সমান। সামান্তরিকের যেকোনো বাহু সংলগ্ন কোণ দুইটির সমষ্টি ১৮০°।

চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল এবং বিপরীত কোণগুলো পরস্পর সমান হলে তাকে সামান্তরিক বলে। সামান্তরিক একটি বিশেষ ধরণের চতুর্ভুজ। সামান্তরিকের কোণগুলো সমকোণ হলে তখন এটি আয়তক্ষেত্র হয়ে যায়। আবার, সামান্তরিকের বাহুগুলো সমান হলে তখন এটি রম্বস আকার ধারণ করে।

একটি সামান্তরিকের চারটি কোণের সমষ্টি চার সমকোণ বা ৩৬০°। যেহেতু সামান্তরিকের যেকোনো বাহুর সন্নিহিত কোণদ্বয়ের সমষ্টি ১৮০°, অতএব ঐ বাহুর বিপরীত বাহুর সন্নিহিত কোণদ্বয়ের সমষ্টিও ১৮০°।
তাহলে, সামান্তরিকের চারটি কোণের সমষ্টি = ১৮০° + ১৮০°।
∴ সামান্তরিকের চারটি কোণের সমষ্টি = ৩৬০°।

সামান্তরিকের সংজ্ঞা ও সামান্তরিক চিত্র ব্যাখ্যা ও বিশ্লেষণ করলে সামান্তরিকের বৈশিষ্ট্য গুলো কি কি তা ফুটে ওঠে। নিচে সামান্তরিকের ৩টি বৈশিষ্ট্য উল্লেখ করা হলো।

• সামান্তরিকের যেকোনো কর্ণ সামান্তরিকটিকে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে।
• সামান্তরিকের একটি কোণের পরিমাপ জানা থাকলে অপর কোণগুলোর পরিমাপ নির্ণয় করা যায়।
• সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।

চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান্তরাল হলে তাকে সামান্তরিক বলে। পক্ষান্তরে, চতুর্ভুজের কোণগুলো সমকোণ হলে তাকে আয়তক্ষেত্র বলে।
সামান্তরিকের কোণগুলো সূক্ষ্মকোণ এবং স্থুলকোণ। কিন্তু আয়তক্ষেত্রের কোণগুলো সমকোণ।
সামান্তরিকের বিপরীত কোণ দুইটির সমষ্টি একটি সূক্ষ্মকোণ বা স্থুলকোণ। কিন্তু, আয়তক্ষেত্রের বিপরীত কোণ দুইটির সমষ্টি একটি সরলকোণ।
সামান্তরিকের সন্নিহিত বাহুদ্বয় পরস্পর লম্ব নয়। কিন্তু আয়তক্ষেত্রের সন্নিহিত বাহুদ্বয় পরস্পর লম্ব।
সামান্তরিকের কর্ণদ্বয় পরস্পর সমান নয়। কিন্তু আয়তক্ষেত্রের কর্ণদ্বয় পরস্পর সমান।
সামান্তরিকের প্রত্যেকটি কর্ণ সামান্তরিকটিকে যে দুইটি ত্রিভুজে বিভক্ত করে তারা এক-একটি সূক্ষ্মকোণী ত্রিভুজ অথবা স্থুলকোণী ত্রিভুজ। কিন্তু আয়তক্ষেত্রের প্রত্যেকটি কর্ণ আয়তক্ষেত্রটিকে যে দুইটি ত্রিভুজে বিভক্ত করে তারা সমকোণী ত্রিভুজ।